【LeetCode-回溯】全排列

题目描述

给定一个 没有重复 数字的序列，返回其所有可能的全排列。
示例：

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

题目链接： https://leetcode-cn.com/problems/permutations/

思路

使用回溯来做。回溯也是在模拟人做排列的方法。例如做[1,2,3]的排列：

1. 第一步有3个数[1,2,3]可以选，先选1，此时结果为[1]；
2. 接下来还有两个数[2,3]可以选，先放2，此时结果为[1,2]；
3. 接下来还有一个数[3]可以选，选3，此时结果为[1,2,3]，结果的长度等于数字的个数，说明找到了一个排列。
4. 回到第2步，有两个数[2,3]可以选，这一次选3，结果为[1,3]；
5. 接下来还有一个数[2]可选，选2，结果为[1,3,2]，结果的长度等于数字的个数，说明找到了一个排列。
6. 以1开头的排列已经搜索结束；回到第1步，有3个数可以选，这一次选[2]，结果为[2]；
7. 使用类似[1]开头的步骤即可(步骤2到步骤5).

上面的过程可以画成一棵树：

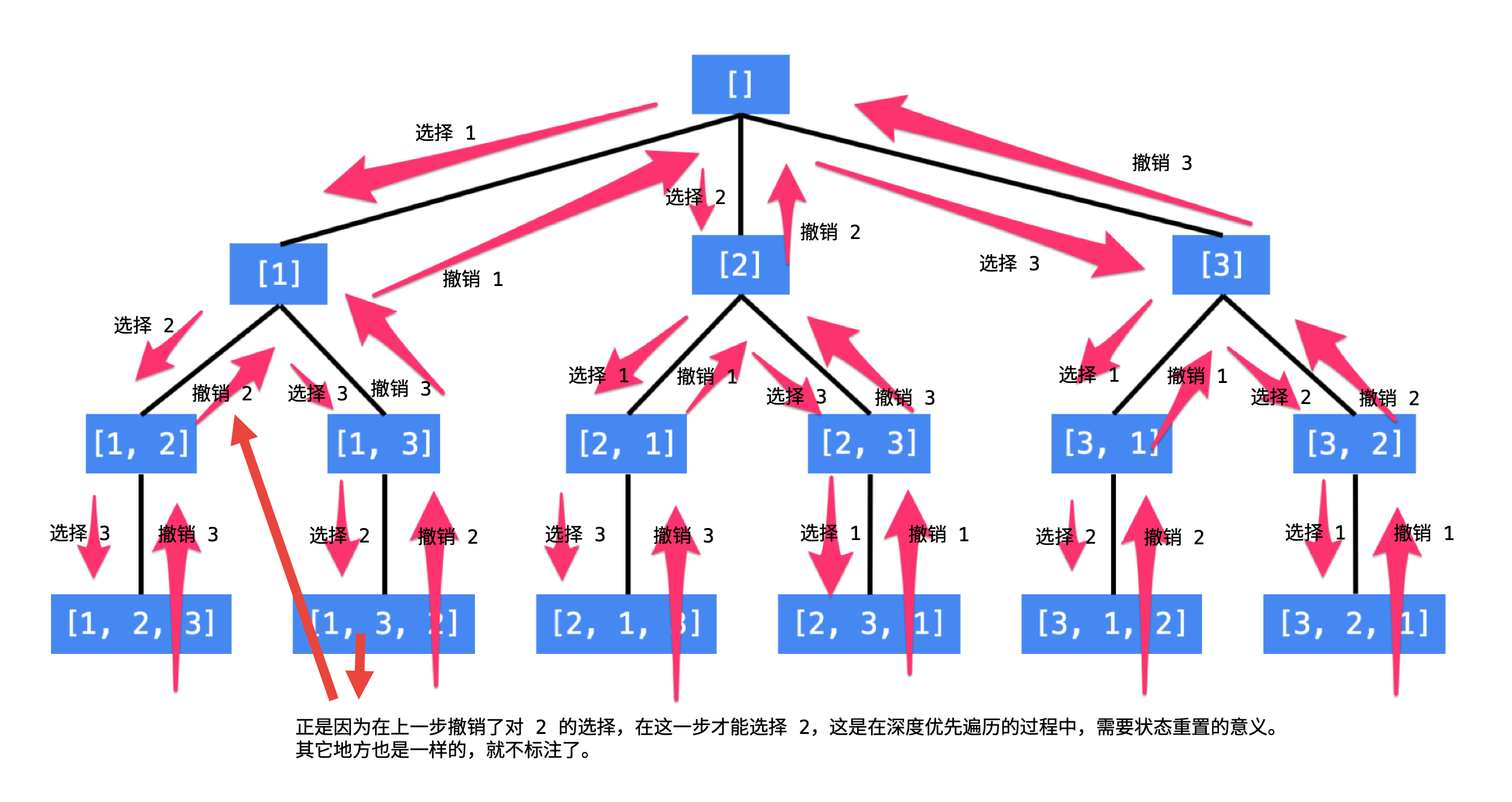
该图来自于这篇文章。回溯就是从树的深层返回到浅层的过程，通过返回浅层，我们可以尝试不同的结果。在做排列的过程中，比如从[1,2,3]中添加1到排列中，那在下一步中1就不能选了，所以还需要一个visit数组来标记一个数字是否已经被添加到了排列当中。代码如下：

class Solution {
public:
    vector<vector<int>> ans;
    vector<vector<int>> permute(vector<int>& nums) {
        if(nums.empty()) return {{}};

        vector<int> track;
        vector<int> visit(nums.size(), 0);
        dfs(nums, 0, track, visit);
        return ans;
    }

    void dfs(vector<int> nums, int start, vector<int> track, vector<int> visit){
        if(track.size()==nums.size()){
            ans.push_back(track);
            return;
        }

        for(int i=0; i<nums.size(); i++){
            if(!visit[i]){
                track.push_back(nums[i]);
                visit[i] = 1;
                dfs(nums, i, track, visit);
                track.pop_back();
                visit[i] = 0;
            }
        }
    }
};

其实上面的代码的dfs函数是不需要start参数的，因为每次都是从数组头开始迭代，这样写是为了和子集这题的写法保持一致，也便于比较。去掉start的写法：

class Solution {
public:
    vector<vector<int>> ans;
    vector<vector<int>> permute(vector<int>& nums) {
        if(nums.empty()) return {{}};

        vector<int> track;
        vector<int> visit(nums.size(), 0);
        dfs(nums, track, visit);
        return ans;
    }

    void dfs(vector<int> nums, vector<int> track, vector<int> visit){
        if(track.size()==nums.size()){
            ans.push_back(track);
            return;
        }

        for(int i=0; i<nums.size(); i++){
            if(!visit[i]){
                track.push_back(nums[i]);
                visit[i] = 1;
                dfs(nums, track, visit);
                track.pop_back();
                visit[i] = 0;
            }
        }
    }
};

总结

子集这一题和求全排列的这题很像，也是使用回溯，但也有区别。把这两题做了，想透了，我觉得应该能对回溯有更清晰的理解。