【PyTorch】PyTorch 中的 dim

PyTorch 中对 tensor 的很多操作如 sum、softmax 等都可以设置 dim 参数用来指定操作在哪一维进行。PyTorch 中的 dim 类似于 numpy 中的 axis，这篇文章来总结一下 PyTorch 中的 dim 操作。

dim 与方括号的关系

创建一个矩阵

a = torch.tensor([[1, 2], [3, 4]])
print(a)

输出

tensor([[1, 2],
        [3, 4]])

因为a是一个矩阵，所以a的左边有 2 个括号

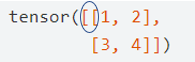
括号之间是嵌套关系，代表了不同的维度。从左往右数，两个括号代表的维度分别是 0 和 1 ，在第 0 维遍历得到向量，在第 1 维遍历得到标量

同样地，对于 3 维 tensor

b = torch.tensor([[[3, 2], [1, 4]], [[5, 6], [7, 8]]])
print(b)

输出

tensor([[[3, 2],
         [1, 4]],

        [[5, 6],
         [7, 8]]])

则 3 个括号代表的维度从左往右分别为 0, 1, 2，在第 0 维遍历得到矩阵，在第 1 维遍历得到向量，在第 2 维遍历得到标量

更详细一点

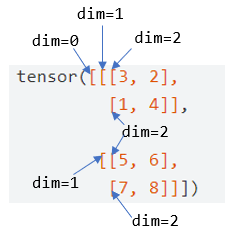
在指定的维度上进行操作

在某一维度求和（或者进行其他操作）就是对该维度中的元素进行求和。
对于矩阵 a

a = torch.tensor([[1, 2], [3, 4]])
print(a)

输出

tensor([[1, 2],
        [3, 4]])

求 a 在第 0 维的和，因为第 0 维代表最外边的括号，括号中的元素为向量[1, 2]，[3, 4]，第 0 维的和就是第 0 维中的元素相加，也就是两个向量[1, 2]，[3, 4]相加，所以结果为

\[[1, 2] + [3, 4] = [4, 6] \]

s = torch.sum(a, dim=0)
print(s)

输出

tensor([4, 6])

可以看到，a 是 2 维矩阵，而相加的结果为 1 维向量，可以使用参数keepdim=True来保证维度数目不变。

s = torch.sum(a, dim=0, keepdim=True)
print(s)

输出

tensor([[4, 6]])

在 a 的第 0 维求和，就是对第 0 维中的元素（向量）进行相加。同样的，对 a 第 1 维求和，就是对 a 第 1 维中的元素（标量）进行相加，a 的第 1 维元素为标量 1，2 和 3，4，则结果为

\[[1+2]=[3], ~ [3+4]=[7] \]

s = torch.sum(a, dim=1)
print(s)

输出

tensor([3, 7])

保持维度不变

s = torch.sum(a, dim=1, keepdim=True)
print(s)

输出

tensor([[3],
        [7]])

对 3 维 tensor 的操作也是这样

b = torch.tensor([[[3, 2], [1, 4]], [[5, 6], [7, 8]]])
print(b)

输出

tensor([[[3, 2],
         [1, 4]],

        [[5, 6],
         [7, 8]]])

将 b 在第 0 维相加，第 0 维为最外层括号，最外层括号中的元素为矩阵[[3, 2], [1, 4]]和[[5, 6], [7, 8]]。在第 0 维求和，就是将第 0 维中的元素（矩阵）相加

\[ \left[ \begin{matrix} 3 & 2 \\ 1 & 4 \\ \end{matrix} \right] + \left[ \begin{matrix} 5 & 6 \\ 7 & 8 \\ \end{matrix} \right] = \left[ \begin{matrix} 8 & 8 \\ 8 & 12 \\ \end{matrix} \right] \]

s = torch.sum(b, dim=0)
print(s)

输出

tensor([[ 8,  8],
        [ 8, 12]])

求 b 在第 1 维的和，就是将 b 第 1 维中的元素[3, 2]和[1, 4], [5, 6]和 [7, 8]相加，所以

\[[3,2]+[1,4]=[4,6], [5,6]+[7,8]=[12,14] \]

s = torch.sum(b, dim=1)
print(s)

输出

tensor([[ 4,  6],
        [12, 14]])

则在 b 的第 2 维求和，就是对标量 3 和 2, 1 和 4, 5 和 6 , 7 和 8 求和

s = torch.sum(b, dim=2)
print(s)

结果为

tensor([[ 5,  5],
        [11, 15]])

除了求和，其他操作也是类似的，如求 b 在指定维度上的最大值

m = torch.max(b, dim=0)
print(m)

b 在第 0 维的最大值是第 0 维中的元素（两个矩阵[[3, 2], [1, 4]]和[[5, 6], [7, 8]]）的最大值，取矩阵对应位置最大值即可
结果为

torch.return_types.max(
values=tensor([[5, 6],
        [7, 8]]),
indices=tensor([[1, 1],
        [1, 1]]))

b 在第 1 维的最大值就是第 1 维元素（4 个（2对）向量）的最大值

m = torch.max(b, dim=1)
print(m)

输出为

torch.return_types.max(
values=tensor([[3, 4],
        [7, 8]]),
indices=tensor([[0, 1],
        [1, 1]]))

b 在第 0 维的最大值就是第 0 为元素（8 个（4 对）标量）的最大值

m = torch.max(b, dim=2)
print(m)

输出

torch.return_types.max(
values=tensor([[3, 4],
        [6, 8]]),
indices=tensor([[0, 1],
        [1, 1]]))

总结

在 tensor 的指定维度操作就是对指定维度包含的元素进行操作，如果想要保持结果的维度不变，设置参数keepdim=True即可。