欧拉函数及模板
什么是欧拉函数
欧拉函数是小于x的整数中与x互质的数的个数,一般用φ(x)表示。特殊的,φ(1)=1。
例如,φ(12)=4 {1,5,7,11}
怎么计算欧拉函数
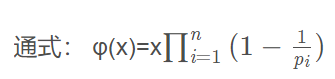
φ(x)=X*(1- 1 p 1 \frac{1}{p1} p11) * (1- 1 p 2 \frac{1}{p2} p21) * … * (1- 1 p i \frac{1}{pi} pi1)
其中p1,p2,p3…pi为x的所有质因数(指能整除给定正整数的质数),x是正整数。
比如x=12,12以内有
1
2
\frac{1}{2}
21的数是2的倍数,还剩下(1,3,5,7,9,11)6个数,这六个数里面又有
1
3
\frac{1}{3}
31的数是3的倍数还剩下(1,5,7,11)4个数,即4个数与12互质,所以φ(12)=4。

欧拉函数三种常用模板
素因数分解求欧拉函数
int phi(int n) {
int ans = n;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
ans -= ans / i;//遇到质因数,即X*1/pi
while (n % i == 0) {
n /= i;
}
}
}
if (n > 1)//若n不为1,则还剩下一位质因子
ans -= ans / n;
return ans;
}
欧拉函数值打表
int phi[1000010];
void euler(int n) {
for (int i=1; i<=n; i++) phi[i]=i;//初始化
for (int i=2; i<=n; i++) {
if (phi[i]==i) { //这代表i是质数
for (int j=i; j<=n; j+=i) {
phi[j]=phi[j]/i*(i-1);//此时将素数i的所有倍数全部运用一下
//欧拉公式中的n*(pi-1)/pi,在这里即phi[j] = phi[j] / i * (i - 1)
}
}
}
}
欧拉筛型欧拉函数
#define MAXN 10000000
int phi[MAXN];//即求出的欧拉函数
int flag[MAXN];
int prime[MAXN];//素数表
void euler(int n) {
phi[1]=1;//1要特判
int num=0;//记录质数总数
for (int i=2; i<=n; i++) {
if (flag[i]==0) { //这代表i是质数
prime[++num]=i;//记录质数
phi[i]=i-1;//质数的欧拉函数为本身减1
}
for (int j=1; j<=num&&prime[j]*i<=n; j++) { //经典的欧拉筛写法
flag[i*prime[j]]=1;//先把这个合数标记掉,每个数只由最小质因子筛一次
if (i%prime[j]==0) {
phi[i*prime[j]]=phi[i]*prime[j];//若prime[j]是i的质因子
//则根据计算公式,i已经包括i*prime[j]的所有质因子
break;//经典欧拉筛的核心语句,这样能保证每个数只会被自己最小的因子筛掉一次
}
else
phi[i*prime[j]]=phi[i]*phi[prime[j]]; //利用了欧拉函数是个积性函数的性质
//φ(m*n)=φ(m)*φ(n)
}
}
}
第一次写博客,分享下自己的初学知识,欢迎大家指出我的错误和对博客内容进行补充,谢谢。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号