动态规划解最长公共子序列(LCS)原理及模板

最长公共子序列 LCS

• 最长公共子序列
• • 1.LCS的概念
  • 2.LCS的规律
• 最长公共子序列的模板
• • 1.动态规划求解LCS模板
  • 2. LCS字符串输出(还原)

最长公共子序列

1.LCS的概念

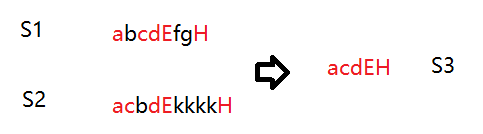
（1）递增 （2）可以连续可以不连续 （3）公共：在S1内，又在S2内 （4）最长：5（acdEH）>4(acdE)…

2.LCS的规律

下列图片来自动态规划解最长公共子序列(LCS)(附详细填表过程)

看了下面6张图，就可以得出上图的结论，从而递推出

if(s1[i-1]==s2[j-1])
    dp[i][j]=dp[i-1][j-1]+1;
else
    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);

最长公共子序列的模板

1.动态规划求解LCS模板

#include<iostream>
#include<algorithm>
using namespace std;
int dp[1005][1005];
int main() {
	string s1,s2;
	while(cin>>s1>>s2) {
		int l1=s1.size();
		int l2=s2.size();
		for(int i=0; i<=l1; i++) {
			dp[0][i]=0;
			dp[i][0]=0;
		}
		for(int i=1; i<=l1; i++) {
			for(int j=1; j<=l2; j++) {
				if(s1[i-1]==s2[j-1])
					dp[i][j]=dp[i-1][j-1]+1;
				else
					dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
			}
		}
		cout<<dp[l1][l2]<<endl;
	}
}

2. LCS字符串输出(还原)

看23-39行，1-23行代码是LCS长度的代码

#include<iostream>
#include<algorithm>
using namespace std;
int dp[1005][1005];
int main(){
    string s1,s2;
    while(cin>>s1>>s2){
        int l1=s1.size();
        int l2=s2.size();
        for(int i=0;i<=l1;i++){
            dp[0][i]=0;
            dp[i][0]=0;
        }
        for(int i=1;i<=l1;i++){
            for(int j=1;j<=l2;j++){
                if(s1[i-1]==s2[j-1])
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            }
        }
        cout<<dp[l1][l2]<<endl;
        int i=l1,j=l2,z=0;
        string s3;
		while(i!=0 && j!=0){
			if(s1[i-1]==s2[j-1]){
				i--;
				j--;
				s3[z++]=s1[i];
			}
			else if(dp[i-1][j]<dp[i][j-1]){
				j--;
			}
			else if(dp[i-1][j]>=dp[i][j-1]){
				i--;
			}
		} 
		for(int i=z-1;i>=0;i--){
			cout<<s3[i];
		}
		cout<<endl;
    }
}