一、变量与函数
1、变量
(1)特殊变量表
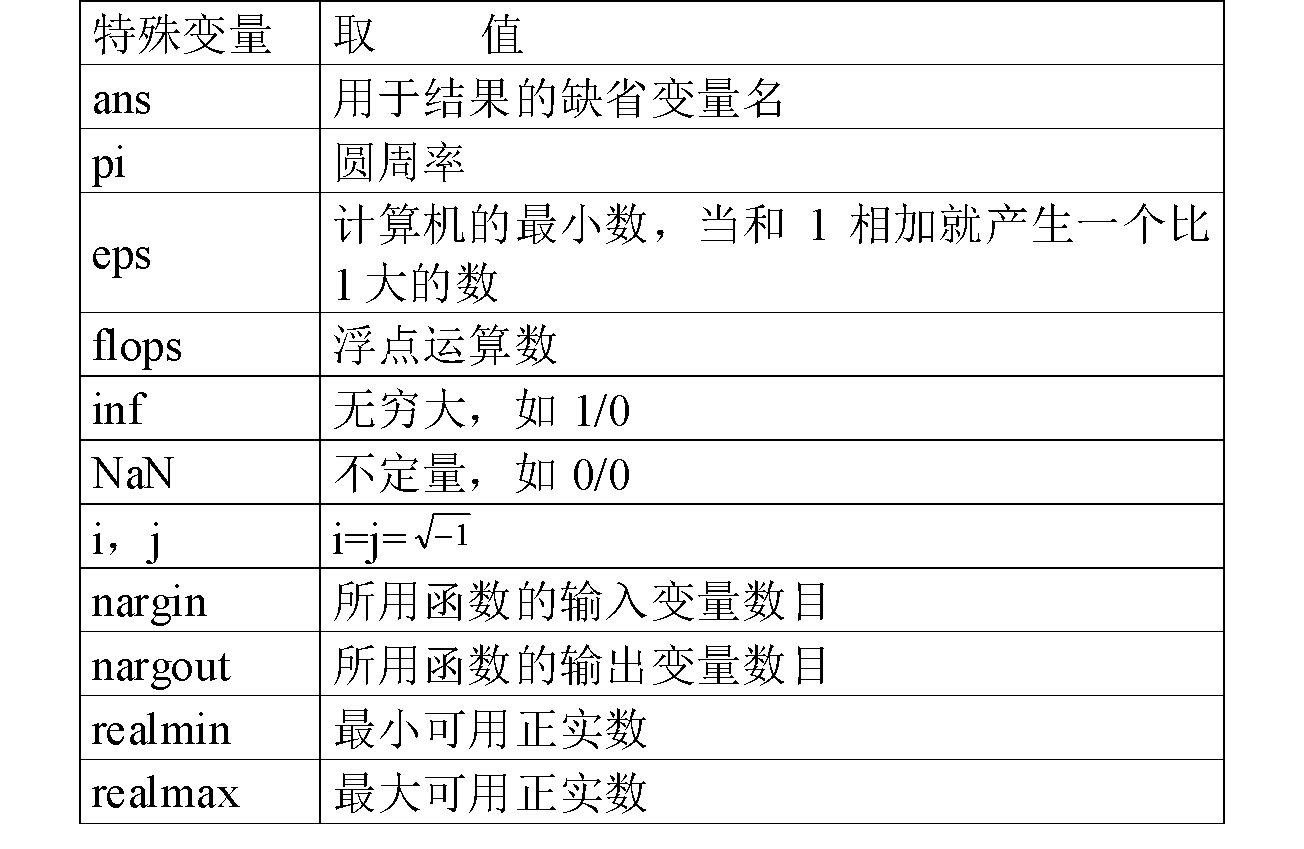
2、数学运算符号及标点符号

(1)MATLAB的每条命令后,若为逗号或无标点符号, 则显示命令的结果;若命令后为分号,则禁止显示结果.
(2)“%” 后面所有文字为注释.
(3) “...”表示续行.
3、数学函数

二、数组
1、创建简单的数组
(1)x=[a b c d e f ] 创建包含指定元素的行向量
(2)x=first:last 创建从first开始,加1计数,到last结束的行向量
(3)x=first:increment:last 创建从first开始,加increment计数,last结束的行向量
(4)x=linspace(first,last,n) 创建从first开始,到last结束,有n个元素的行向量
(5)x=logspace(first,last,n) 创建从开始,到结束,有n个元素的对数分隔行向量.
2、 数组元素的访问
(1)访问一个元素: x(i)表示访问数组x的第i个元素.
(2)访问一块元素: x(a :b :c)表示访问数组x的从第a个元素开始,以步长为b到第c个元素(但不超过c),b可以为负数,b缺损时为1.
(3)直接使用元素编址序号. x([a b c d]) 表示提取数组x的第a、b、c、d个元素构成一个新的数组 [x(a) x(b) x(c) x(d)].
3、数组的运算
(1)标量-数组运算
数组对标量的加、减、乘、除、乘方是数组的每个元素对该标量施加相应的加、减、乘、除、乘方运算.
设:a=[a1,a2,…,an], c=标量
则:a+c=[a1+c,a2+c,…,an+c]
a.*c=[a1*c,a2*c,…,an*c]
a./c= [a1/c,a2/c,…,an/c](右除)
a.\c= [c/a1,c/a2,…,c/an] (左除)
a.^c= [a1^c,a2^c,…,an^c]
c.^a= [c^a1,c^a2,…,c^an]
(2)数组-数组运算
当两个数组有相同维数时,加、减、乘、除、幂运算可按元素对元素方式进行的,不同大小或维数的数组是不能进行运算的.
设:a=[a1,a2,…,an], b=[b1,b2,…,bn]
则:a+b= [a1+b1,a2+b2,…,an+bn]
a.*b= [a1*b1,a2*b2,…,an*bn]
a./b= [a1/b1,a2/b2,…,an/bn]
a.\b=[b1/a1,b2/a2,…,bn/an]
a.^b=[a1^b1,a2^b2,…,an^bn]
三、 矩阵
1、矩阵的建立
b=zeros(m,n) 产生一个m行、n列的零矩阵
c=ones(m,n) 产生一个m行、n列的元素全为1的矩阵
d=eye(m,n) 产生一个m行、n列的单位矩阵
2、矩阵中元素的操作
(1)矩阵A的第r行:A(r,:)
(2)矩阵A的第r列:A(:,r)
(3)依次提取矩阵A的每一列,将A拉伸为一个列向量:A(:)
(4)取矩阵A的第i1~i2行、第j1~j2列构成新矩阵:A(i1:i2, j1:j2)
(5)以逆序提取矩阵A的第i1~i2行,构成新矩阵:A(i2:-1:i1,:)
(6)以逆序提取矩阵A的第j1~j2列,构成新矩阵:A(:, j2:-1:j1 )
(7)删除A的第i1~i2行,构成新矩阵:A(i1:i2,:)=[ ]
(8)删除A的第j1~j2列,构成新矩阵:A(:, j1:j2)=[ ]
(9)将矩阵A和B拼接成新矩阵:[A B];[A;B]
3、矩阵的运算
(1)标量-矩阵运算
同标量-数组运算。
(2)矩阵-矩阵运算
[1] 元素对元素的运算,同数组-数组运算。
[2]矩阵运算:
矩阵加法:A+B
矩阵乘法:A*B
方阵的行列式:det(A)
方阵的逆:inv(A)
方阵的特征值与特征向量:[V,D]=eig[A]
关系与逻辑运算
2、逻辑运算符

第一步:如何将数据导入matlab中
参考链接:
Excel 详情参考《MATLAB在数学建模中的应用》第3页
安装Excel link插件,实现Excel与Matlab的互联
记事本 详情参考《MATLAB在数学建模中的应用》第3-5页
第二步:学会如何给数据制表
grid on 是matlab中的一种函数,表示在画图的时候添加网格线。
hold on 保持当前图形窗口
axis 设置坐标轴的最小最大值 用法:axis([xmin,xmax,ymin,ymax])
axis equal:纵、横坐标轴采用等长刻度
axis tight是使坐标系的最大值和最小值和你的数据范围一致!
第三步:学会如何用matlab画图(呈现数据的模型类型),详情参考:Matlab建模训练3 图形绘制、matlab绘制二元函数图形、matlab画图怎么设置线条类型和颜色
如何解决matlab画图很丑的问题?
1、蒙特卡罗算法(该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟可以来检验自己模型的正确性,是比赛时必用的方法)
2、数据拟合、参数估计、插值等数据处理算法(比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用 Matlab 作为工具)
插值和拟合
拉格朗日插值、
牛顿(Newton)插值及其MATLAB程序、
matlab_最小二乘法数据拟合、Matlab随笔之插值与拟合(下)
3、线性规划、整数规划、多元规划、二次规划等规划类问题(建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用 Lindo、Lingo 软件实现)利用Lingo求解整数规划及非线性规划问题
线性规划(求最小值) 目标函数为线性,具体程序参考《MATLAB在数学建模中的应用》19-21页
x = linprog( c , A , b , Aeq , beq , lb , ub , x0 )是求解线性规划问题的命令。 c是目标函数的系数向量,A是不等式约束AX<=b的系数矩阵,b是不等式约束AX<=b的常数项 Aeq是等式约束AeqX=beq的系数矩阵,beq是等式约束AeqX=beq的常数项,lb是X的下限,ub是X的上限,X是向量[x1,x2,...xn]即决策变量。 指定迭代的初始值x0; 如果模型中不包含不等式约束条件,可用[]代替A和b表示缺省;如果没有等式约束条件,可用[]代替Aeq和beq表示缺省;如果某个xi无下界或上界,可以设定lb(i)=-inf或ub(i)=inf; 用[x , Fval]代替上述各命令行中左边的x,则可得到在最优解x处的函数值Fval;
非线性规划(包括多元) 目标函数为非线性,具体程序参考《MATLAB在数学建模中的应用》23页
fmincon(有约束)&fminunc(无约束)&fminbnd(求目标函数在区间范围的最小值)用法,详情参考:Matlab fmincon函数用法、Matlab函数fminunc/fminbnd/fmincon求解工程优化问题
二次规划 目标函数为非线性,约束条件全为线性,具体程序参考《MATLAB在数学建模中的应用》23-25页
详情参考:quadprog用法 二次规划问题和MATLAB函数quadprog的使用
整数规划 变量限制为整数,具体程序参考《MATLAB在数学建模中的应用》27-29页
详情参考:用lingo求解整数规划
0-1整数规划 利用Lingo求解整数规划及非线性规划问题
4、图论算法(这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备)
5、动态规划、回溯搜索、分治算法、分支定界等计算机算法(这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中)
6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法(这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用)
遗传算法(simple genetic algorithm),具体程序参考《MATLAB在数学建模中的应用》用法说明:49-52页 例子一:53-59页
神经网络 BP(back propagation)算法,具体程序参考数据预测之BP神经网络具体应用以及matlab代码、如何利用matlab做BP神经网络分析(包括利用matlab神经网络工具箱)、MATLAB 中BP神经网络算法的实现、《MATLAB在数学建模中的应用》用法说明:109-115页 例子一:117-123页 例子二:124-130页
数据归一化参考:matlab premnmx归一化函数的使用
粒子群算法(particle swam optimization),具体程序参考《MATLAB在数学建模中的应用》 64-68页
基于PSO算法和BP算法训练神经网络,具体程序参考《MATLAB在数学建模中的应用》 64-68页
解释:BP容易陷入局部最小值,PSO在无约束多规划问题方面有很大优越性。
模拟退火算法(求最小值),求解背包问题、指派问题的0-1编码、调度问题的自然数编码、用于连续函数优化的实数编码、组合优化问题(旅行商TSP问题,如物流配送、计算机网络、电子地图、电气路线等方面,早期用分支定界法、线性规划法和动态规划法(变量数目在100个以下)),具体程序参考《MATLAB在数学建模中的应用》 87-92页
模拟退火程序包ASA(adaptive simulated annealing),具体使用说明参考《MATLAB在数学建模中的应用》 93-95页
7、网格算法和穷举法(网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具)
8、一些连续离散化方法(很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的)
9、数值分析算法(如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用)
10、图象处理算法(赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用 Matlab 进行处理)
产生随机数 rand
灰色预测,具体程序参考《MATLAB在数学建模中的应用》27-29页
灰色预测适用于小样本的预测,常用来解决一些不确定性的问题。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。



