「2017 Multi-University Training Contest 2」2017多校训练2
1001 Is Derek lying
给出两个人选择题的回答,问得分分别为x和y是否可能。(\(1\le N \le 80000,0\le x,y \le N\))
答案相同的部分,得分一定一样;答案不同的部分(dif个),是造成差距的地方。差距不可能超过不同的个数。分低者(y分)若成绩超过相同部分,那么不同部分也拿了分(y-sam)。分高者最多还能拿剩下的不同部分的分(dif-(y-sam))。也就是最大分差为dif-(y-sam)-(y-sam)。
#include <bits/stdc++.h>
#define N 100001
using namespace std;
int t;
int n,x,y;
char s1[N],s2[N];
int main(){
scanf("%d",&t);
while(t--){
scanf("%d%d%d%s%s",&n,&x,&y,s1,s2);
if(x<y)swap(x,y);
int dif=0,sam=0;
for(int i=0;i<n;++i)if(s1[i]!=s2[i])++dif;else ++sam;
if(x-y>dif||y>sam&&dif-(y-sam)*2<x-y)puts("Lying");
else puts("Not lying");
}
return 0;
}
1002 hash(哈希)
用函数f(i,j)生成了一个\(1e6*1e6\)的随机01矩阵。给你\(1000*1000\)的01矩阵,求其左上角在原矩阵中的位置。
每隔L行L列生成一个\(K*K\)的识别矩阵,要令给出的矩阵中一定存在这个识别矩阵,根据容斥原理,有\(K+L\le 1000\),令K为7,得到L。然后找出了识别矩阵在给定矩阵中的位置,就能判断给定矩阵在原矩阵中的位置了。
#include <bits/stdc++.h>
#define N 1000
#define K 7
using namespace std;
#define LL long long
int t,cas;
char s[N+1][N+1];
map<unsigned LL,pair<int,int> >haxi;
inline unsigned sfr(unsigned h,unsigned x){
return h>>x;
}
int f(LL i,LL j){
LL w=i*1000000ll+j;
int h=0;
for(int k=0;k<5;++k){
h+=(int)((w>>(8*k))&255);
h+=(h<<10);
h^=sfr(h,6);
}
h+=h<<3;
h^=sfr(h,11);
h+=h<<15;
return sfr(h,27)&1;
}
int main(){
for(int i=1;i<=1000000;i+=N-K)
for(int j=1;j<=1000000;j+=N-K){
unsigned LL ss=13;
unsigned LL hx=0;
for(int k=0;k<K;++k)
for(int g=0;g<K;++g){
hx=hx*ss+f(i+k,j+g);
ss*=13;
}
haxi[hx]=make_pair(i,j);
}
scanf("%d",&t);
int x=0,y=0;
while(t--){
for(int i=0;i<N;++i)scanf("%s",s[i]);
bool fnd=false;
for(int i=0;i<N;++i){
for(int j=0;j<N;++j){
unsigned LL ss=13;
unsigned LL hx=0;
for(int k=0;k<K;++k)
for(int g=0;g<K;++g){
hx=hx*ss+s[i+k][j+g]-'0';
ss*=13;
}
if(haxi.find(hx)!=haxi.end()){
fnd=true;
x=haxi[hx].first-i;
y=haxi[hx].second-j;
break;
}
}
if(fnd)break;
}
printf("Case #%d :%d %d\n",++cas,x,y);
}
return 0;
}
1003 Maximum Sequence(贪心)
给定数组a[1..n]和b[1..n],b[i]在[1~n]内。要得到a[n+1..2n],每次选b数组的一个,令a[i]为j=b[k]到i-1位置中最大的a[j]-j。求a[n+1..2n]总和最大值。
每次b选最小的,这次的a[i]就能尽量大,而b[k]到i-1的位置中最大的a[j]-j,早晚要加到总和中,先选不会更差。
对a预处理为a[i]-i。b桶排序。剩下就是每次选出b[k]到i-1位置中最大值。a[i..n]中最大值可以用一个数组记录起来,即后缀最大值。然后a[n+1..i]最大值可以用一个变量维护。每次选两个区间的最大值作为当前a[i]的值。
#include <bits/stdc++.h>
#define ll long long
#define N 250001
#define mem(a,b) memset(a,b,sizeof (a))
#define INF 0x3f3f3f3f
#define LL long long
const LL MOD=(1e9+7);
using namespace std;
int a[N],b[N];
int c[N];
int n;
int main(){
while(~scanf("%d",&n)){
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
a[i]-=i;
}
c[n]=a[n];
for(int i=n-1;i;--i)
c[i]=max(c[i+1],a[i]);
mem(b,0);
for(int i=1;i<=n;++i){
int c;
scanf("%d",&c);
++b[c];
}
LL ans=0;
int j=1;
int maxs=-INF;
for(int i=1;i<=n;++i){
while(b[j]==0) ++j;
--b[j];
int now=max(c[j],maxs);
ans=(ans+now)%MOD;
maxs=max(maxs,now-n-i);
}
printf("%lld\n",ans);
}
return 0;
}
1004 Puzzle(逆序对数)
一个\(N*M\)的拼图游戏里有\(N*M-1\)片拼图,一个空格。现在重排拼图:每轮将剩下的第1片、第P+1片,第2P+1片...顺序(上到下,左到右)放入拼图中。问得到的拼图是否可以拼回“1,2,3,...nm-1,空格”的顺序。
拼图游戏不会改变逆序对数的奇偶性。所以逆序对数是偶数就是YES,否则是NO。
#include<bits/stdc++.h>
using namespace std;
int t,n,m,p;
int main(){
scanf("%d",&t);
while(t--){
scanf("%d%d%d",&n,&m,&p);
int tot=n*m-1, rev=0;
while(tot>p){
int num=(tot-1)/p+1;
tot-=num;
rev+=num*(num-1)/2*(p-1);
}
puts(rev&1?"NO":"YES");
}
return 0;
}
1005 Sdjpx Is Happy(区间dp)
题意:
将数组a划分K个块,每个块内的数排序,允许交换一对块的位置。问K最大是多少。
题解:
\(f[i][j]\)表示[i,j]不允许交换最多能划分为多少个块。
\(mi[i][j],ma[i][j]\) 分别表示区间[i,j]内的最小值、最大值。
枚举左边的一块要交换的为[i,j],右边一块的右端点就必须是\(ma[i][j]\)。再枚举右边一块的左端点。
#include <bits/stdc++.h>
#define N 3001
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
int t,n;
int mi[N][N],ma[N][N],f[N][N],r[N];
int a[N];
int main(){
scanf("%d",&t);
while(t--){
scanf("%d",&n);
mem(f,0);
for(int i=1;i<=n;++i)
scanf("%d",a+i);
for(int i=1;i<=n;++i){
mi[i][i]=ma[i][i]=a[i];
r[i]=i;
f[i][i]=1;
for(int j=i+1;j<=n;++j){
mi[i][j]=min(mi[i][j-1],a[j]);
ma[i][j]=max(ma[i][j-1],a[j]);
}
}
for(int l=2;l<=n;++l){
for(int i=1;i<=n-l+1;++i){
int j=i+l-1;
if(ma[i][j]-mi[i][j]==l-1){
if(mi[i][r[i]]==mi[i][j])
f[i][j]=f[i][r[i]]+f[r[i]+1][j];
else
f[i][j]=1;
r[i]=j;
}else{
f[i][j]=0;
}
}
}
int res=f[1][n];
for(int i=1;i<=n;++i)
for(int j=i;j<=n;++j)
if(f[i][j]&&(i==1||f[1][i-1]&&mi[1][i-1]==1)){
int jj=ma[i][j];
if(jj==n||ma[jj+1][n]==n&&f[jj+1][n])
for(int ii=jj; ii>j; --ii)
if(f[ii][jj]&&mi[ii][jj]==i)
res=max(res,f[1][i-1]+f[j+1][ii-1]+f[jj+1][n]+2);
}
printf("%d\n",res);
}
return 0;
}
1006 Funny Function(递推)
题意:
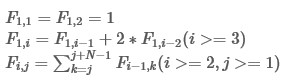
求\(F_{m,1}\) 模 1e9+7.
题解:
由第二个式子的特征方程解得 \(F_{1,i}=\frac{2^n-(-1)^n}{3}\)
由第三个式子知\(F_{i,j}\) 是\(F_{i-1,j}\)开始的N项之和。将\(2^n\)和\((-1)^n\)分别计算就得到两个等比数列求和。于是\(F_{m,1}=(2\cdot (2^n-1)^{m-1}+(n\%2?-1:0))/3\),再特判m==1的情况 。
//不会官方题解的推法。
代码:
#include <bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof (a))
using namespace std;
typedef long long ll;
const ll MOD=(1e9+7);
int t;
ll n,m;
ll qpow(ll a,ll b){
a%=MOD;
ll ans=1;
for(;b;b>>=1,a=a*a%MOD)
if(b&1)ans=ans*a%MOD;
return ans;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>t;
while(t--){
cin>>n>>m;
ll ans=(qpow(2,n)-1+MOD)%MOD;
ans=qpow(ans,m-1)*2%MOD;
if(m==1){
puts("1");
continue;
}
ll chuyi3=qpow(3,MOD-2)%MOD;
if(n&1){
cout<<(ans+1)*chuyi3%MOD<<endl;
}else{
cout<<ans*chuyi3%MOD<<endl;
}
}
return 0;
}
1007 If the starlight never fade(原根,gcd求和)
HDU6051-If the starlight never fade
题意:
f(i)为满足\((x+y)^i\equiv x^i \%p\)且\(1\le x <p, 1\le y \le m\)的x,y有几对。
现在要求计算\(\sum_{i=1}^{p-1}i\cdot f(i)\)。(\(1\le m< p-1, 2\le p\le 1e9+7\))。答案对1e9+7取模。
题解:
看到\(x^i\%p\) ,要想到原根。
设g为模p原根,存在唯一的整数a,b使得\(x=g^a, y=g^b,1\le a,b<p\)
\((x+y)^i\equiv x^i \%p \Leftrightarrow (g^a+g^b)^i\equiv g^{ai}\%p \Leftrightarrow (1+g^{b-a})^i\equiv 1 \%p\)
后面一个推导是两边都乘上了\(g^{-ai}\%p\)。
因为\(1+g^{b-a}\ge 2\),故存在唯一的整数k使得\(g^k=(1+g^{b-a})\%p,1\le k< p\),带入上式得\(g^{ki}\equiv 1\%p\)。
由原根的性质,g的幂 模p的余数是一个0~p-1的循环。\(g^{ki}\equiv g^0 \%p\),所以\(ki\equiv 0 \%(p-1)\)
k的取值就是$\frac {p-1}{gcd(i,p-1)} $乘以1、乘以2、...、乘以gcd(i,p-1)-1共gcd(i,p-1)-1个。(因为ki是p-1的倍数,k里至少要有p-1有但是i没有的因子。)
对于固定的y来说 \(x\equiv y(g^k-1)^{-1}\%p\),也就有gcd(i,p-1)-1个x的取值。
因此\(f(i)=m\sum_{i=1}^{p-1}(i\cdot gcd(p-1,i)-i)\)
接着右边的-i的求和可以直接计算。\(i\cdot gcd(p-1,i)\)的求和可以枚举gcd为d,求和为\(\sum_{d|p-1}d\cdot d\cdot \sum_{k=1}^{k=\frac{p-1}{d}}(k\cdot [gcd(k,\frac{p-1}{d})=1])\)。这里就是说\(k\cdot d=i\),d是gcd(p-1,i),k和\(\frac {p-1}{d}\)不能有公因子。
hints:
代码:
#include <bits/stdc++.h>
#define ll long long
const ll M=1e9+7;
using namespace std;
int t,cas;
ll p,m;
ll phi(int x){
ll res=x;
for(int i=2;i*i<=x;++i)
if(x%i==0){
res=res/i*(i-1);
while(x%i==0)x/=i;
}
if(x>1)res=res/x*(x-1);
return res;
}
int main(){
scanf("%d",&t);
while(t--){
scanf("%lld%lld",&m,&p);
ll ans=M-p*(p-1)/2%M;
/*for(ll i=1;i<p;++i){
ans+=__gcd(i,p-1)*i;
ans%=M;
}*/
--p;
for(int i=1;i*i<=p;++i)
if(p%i==0){
int j=p/i;
ans+=(1LL*j*phi(j)+(j==1))/2%M*i*i%M;
if(i!=j)
ans+=(1LL*i*phi(i)+(i==1))/2%M*j*j%M;
ans%=M;
}
ans=ans*m%M;
printf("Case #%d: %lld\n",++cas,ans);
}
return 0;
}
1008 To my boyfriend(子矩阵颜色数期望)
题意:
给你一个n行m列的矩阵,随机选一个子矩阵,求它不同数字的个数的期望。
题解:
把不同数字当不同颜色考虑,比较生动。
期望=(\(\sum\)每种颜色贡献了多少个子矩阵)/总子矩阵数
为了不重复计算,每个格子只在它作为子矩阵里同色格子的最上面的最左边时才算它的贡献。
然后枚举子矩阵上边界,计算左上角和右下角的选择方案数,乘起来。
上边界确定,则左上角可以从该行“当前格子所在列左边最近的同色列”+1的位置到“当前格子所在列”这些位置中选择;
右下角可以从当前格子所在行到第n行,这些行的“当前格子所在列”到该行“当前格子所在列右边最近的同色列”-1的位置中选择。
我们将格子先按颜色,然后按x,最后按y关键字排序。可以快速找出上面要求的位置。
ps.注意题目要求保留9位小数
代码:
#include <bits/stdc++.h>
using namespace std;
struct Grid{
int c,x,y;
}g[10001];
bool cmp(const Grid &a,const Grid &b){
if(a.c==b.c){
if(a.x==b.x)return a.y<b.y;
return a.x<b.x;
}
return a.c<b.c;
}
int cnt;
int t,n,m;
int main(){
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&m);
cnt=0;
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j){
int c;
scanf("%d",&c);
g[cnt++]=(Grid){c,i,j};
}
sort(g,g+cnt,cmp);
double num=0;
for(int c=0;c<cnt;++c){//第c个格子
int left=1,right=m;//左上角的左边界,右下角的右边界
for(int up=g[c].x,t=c-1;up;--up){//上边界,即左上角的所在行
for(;t>=0&&g[t].x==up&&g[t].c==g[c].c;--t){//往前枚举第up行的同色格子
if(g[t].y>g[c].y)
right=min(right,g[t].y-1);
else
left=max(left,g[t].y+1);
}
if(up==g[c].x)right=m;//如果是同一行,右边界为m
num+=(g[c].y-left+1)*(right-g[c].y+1)*(n-g[c].x+1);//累加贡献的矩阵数
}
}
printf("%.9f\n", num/((n+1)*n/2*(m+1)*m/2));//除以总子矩阵数
}
return 0;
}
1009 TrickGCD(莫比乌斯函数)
题意:
给你数组A[1..n],问有多少个数组B[1..n]满足所有区间的gcd都不小于2,且\(B_i\le A_i\)。n和A都不超过1e5
题解:
g枚举gcd从2到min{Ai}。一般会想枚举每个Ai中有多少个g的倍数即Ai/g,然后乘起来就是当前g的所有方案数,为了不重复计算,需要算莫比乌斯函数,相当于容斥原理了一下。但是这样会超时的,所以枚举g的倍数l,就变成除以g为l的有多少个Ai,预处理出pre[i](代表1~i出现的次数)。
这题注意上界要和N取min
代码:
#include <bits/stdc++.h>
#define N 100001
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const ll MOD=1e9+7;
int mu[N];
int pr[N],cnt;
bool isp[N];
void init(){
mem(isp,true);
for(int i=2;i<N;++i){
if(isp[i]){
mu[i]=-1;
pr[cnt++]=i;
}
for(int j=0;j<cnt&&pr[j]*i<N;++j){
isp[i*pr[j]]=false;
if(i%pr[j]==0)break;
mu[i*pr[j]]=-mu[i];
}
}
}
ll qpow(ll x,int b){
ll ans=1;
for(;b;x=x*x%MOD,b>>=1)if(b&1)ans=ans*x%MOD;
return ans;
}
int t,cas,n,m;
int num[N];
int main(){
init();
scanf("%d",&t);
while(t--){
scanf("%d",&n);
mem(num,0);
for(int i=0;i<n;++i){
int x;
scanf("%d",&x);
m=i?min(m,x):x;
++num[x];
}
for(int i=1;i<N;++i)
num[i]+=num[i-1];
ll ans=0;
for(int g=2;g<=m;++g){
ll tmp=1;
for(int i=g,l=1;i<N;i+=g,++l){
int c=num[min(i+g,N)-1]-num[i-1];
tmp=tmp*qpow(l,c)%MOD;
}
ans=((ans-tmp*mu[g])%MOD+MOD)%MOD;
}
printf("Case #%d: %lld\n",++cas,ans);
}
return 0;
}
1011 Regular polygon(正多边形计数)
题意:
500个格点(坐标绝对值100以内),问有多少个正多边形。
题解:
只可能是正方形,枚举两个点,然后计算出另外两个点坐标,判断是否存在。
#include <bits/stdc++.h>
#define N 501
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
struct P{
int x,y;
}p[N];
int n;
bool b[N][N];
bool ck(int x,int y){
return x>=0&&x<N&&y>=0&&y<N&&b[x][y];
}
int main(){
while(~scanf("%d",&n)){
mem(b,0);
for(int i=1;i<=n;++i){
int x,y;
scanf("%d%d",&x,&y);
x+=100,y+=100;
b[x][y]=1;p[i]=(P){x,y};
}
int ans=0;
for(int i=1;i<n;++i)
for(int j=i+1;j<=n;++j){
int dx=p[i].x-p[j].x,dy=p[i].y-p[j].y;
for(int k=-1;k<2;k+=2){
int cx=p[i].x+k*dy,cy=p[i].y-k*dx;
int nx=p[j].x+k*dy,ny=p[j].y-k*dx;
if(ck(cx,cy)&&ck(nx,ny))ans++;
}
}
printf("%d\n",ans/4);
}
return 0;
}
┆凉┆暖┆降┆等┆幸┆我┆我┆里┆将┆ ┆可┆有┆谦┆戮┆那┆ ┆大┆始┆ ┆然┆
┆薄┆一┆临┆你┆的┆还┆没┆ ┆来┆ ┆是┆来┆逊┆没┆些┆ ┆雁┆终┆ ┆而┆
┆ ┆暖┆ ┆如┆地┆站┆有┆ ┆也┆ ┆我┆ ┆的┆有┆精┆ ┆也┆没┆ ┆你┆
┆ ┆这┆ ┆试┆方┆在┆逃┆ ┆会┆ ┆在┆ ┆清┆来┆准┆ ┆没┆有┆ ┆没┆
┆ ┆生┆ ┆探┆ ┆最┆避┆ ┆在┆ ┆这┆ ┆晨┆ ┆的┆ ┆有┆来┆ ┆有┆
┆ ┆之┆ ┆般┆ ┆不┆ ┆ ┆这┆ ┆里┆ ┆没┆ ┆杀┆ ┆来┆ ┆ ┆来┆


 浙公网安备 33010602011771号
浙公网安备 33010602011771号