动态规划(最长公共子序列)
有一个经典问题:
长度为n的序列,插入若干数字后,让其形成回文串。求插入的数字最少的个数p
p=n-最长公共子序列
最长公共子序列可以利用动态规划的思想,具体可以用下面这个图来表示:
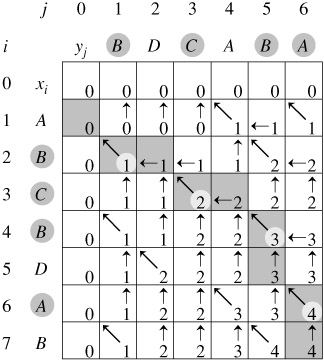
//求最长公共子序列 for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(s[i]==s[n-j+1])//正串和逆序串 dp[i][j]=dp[i-1][j-1]+1; else dp[i][j]=max(dp[i-1][j],dp[i][j-1]); } }
将序列打印出来
#include<iostream> #include<cstdio> #include<string> using namespace std; int dp[100][100]; int main() { //防止数组越界,添加一下前导符 string s="0BDCABA"; string t="1ABCBDAB"; int len1=s.length(); int len2=t.length(); for(int i=1;i<len1;i++) { for(int j=1;j<len2;j++) { if(s[i]==t[j]) dp[i][j]=dp[i-1][j-1]+1; else dp[i][j]=max(dp[i-1][j],dp[i][j-1]); } } cout<<dp[len1-1][len2-1]<<endl; int p=len1-1,q=len2-1; while(p>=1&&q>=1) { if(s[p]==t[q]) { cout<<s[p]<<" "; p-=1; q-=1; } else if(dp[p-1][q]>=dp[p][q-1]) { p-=1; } else q-=1; } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号