交叉熵和 torch.nn.CrossEntropyLoss()

最近又回实验室了，开始把空闲将近半年忘记的东西慢慢找回来。先把之前这边用英文写的介绍交叉熵的文章翻译了。

背景

In classification, the most common setup is with one input, and the output is a vector of size of #classes. The predicted class of the input will be the corresponding class with the largest entry in the last network layer.

In classification task, cross-entropy loss （交叉熵） is the most common loss function you will see to train such networks. Cross-entropy loss can be written in the equation below. For example, there is a 3-class CNN. The output (\(y\)) from the last fully-connected layer is a \((3 \times 1)\) tensor. There is another vector \(y^{'}\) with the same dimension which refers to the ground-truth label of the input.

多分类问题里（单对象单标签），一般问题的setup都是一个输入，然后对应的输出是一个vector，这个vector的长度等于总共类别的个数。输入进入到训练好的网络里，predicted class就是输出层里值最大的那个entry对应的标签。

交叉熵在多分类神经网络训练中用的最多的loss function（损失函数）。据一个很简单的例子，我们有一个三分类问题，对于一个input \(x\)，神经网络最后一层的output (\(y\))是一个\((3 \times 1)\)的向量。然后这个\(x\)对应的ground-truth(\(y^{'}\) )也是一个\((3 \times 1)\)的向量。

交叉熵

Say, 3 classes are 0, 1 and 2 respectively. And the input belongs to class 0. The network output \((y)\) is then something like \((3.8,-0.2,0.45)\) if this is a reasonably trained classifier. Ground-truth vector (\(y^{'}\)) for this input is \((1,0,0)\). So for an input of class 0, we have:

三个类别分别是类别0，1和2。这里让input \(x\)属于类别0。所以ground-truth(\(y^{'}\) ) 就等于\((1,0,0)\), 让网络的预测输出等于\((3.8,-0.2,0.45)\)，举一个很简单的例子：

\[y = (3.8,-0.2,0.45), \space y^{'} = (1,0,0) \]

交叉熵损失的定义如下公式所示(在上面的列子里，i是从0到2的)：

The formal definition of cross-entropy loss is as following, with i ranging from 0 to 2:

\[H (y,y^{'})= -\sum_i {y_i^{'}}\log(softmax(y_i)) \]

Softmax

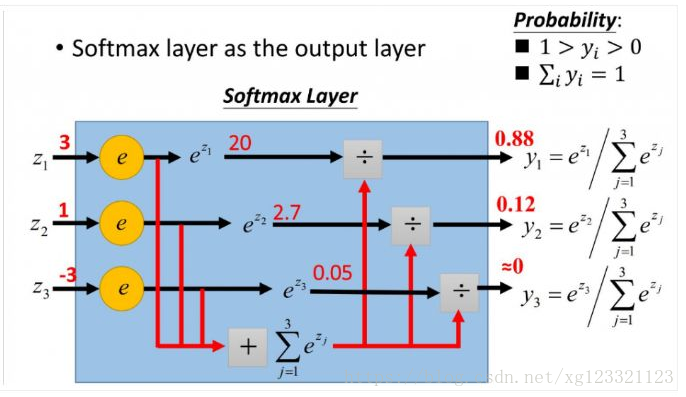
The computation of softmax can be represented by a softmax layer demonstrated by the diagram below. Note that the input to the softmax layer (z) in the diagram is our vector y mentioned above.

softmax的计算可以在下图找到。注意在图里，softmax的输入\((3,1,-3)\) 是神经网络最后一个fc层的输出(\(y\))。

softmax常用于多分类过程中，它将多个神经元的输出，归一化到( 0, 1) 区间内，因此Softmax的输出可以看成概率，从而来进行多分类。

nn.CrossEntropyLoss() in Pytorch

Essentially, the cross-entropy only has one term. Because there is only the probability of the ground-truth class that is left in the cross-entropy loss equation:

其实归根结底，交叉熵损失的计算值需要一个term。这个term就是在softmax输出层中找到ground-truth里正确标签对应的那个entry \(j\) —>(\(\log(softmax(y_j))\))。

\[H (y,y^{'})= -{y_j^{'}}\log(softmax(y_j)) \]

Here, j corresponds to the ground-truth class. And \(y_i = 1\) only when \(i=j\) otherwise \(y_i = 0\).

因为entry \(j\)对应的是ground-truth里正确的class。只有在\(i=j\)的时候才\(y_i = 1\)，其他时候都等于0。

In the script below, the result of torch.nn.CrossEntropyLoss() is compared with hand-calculated result of cross-entropy loss. It is testified that torch.nn.CrossEntropyLoss() takes the input of raw network output layer, which means the computation of softmax layder in included in the function. So when we construct the network in pytorch, there is no need to append an extra softmax layer after the final fully-connected layer.

import torchs
import torch.nn as nn
import math

output = torch.randn(1, 5, requires_grad = True) #假设是网络的最后一层，5分类
label = torch.empty(1, dtype=torch.long).random_(5) # 0 - 4， 任意选取一个分类

print ('Network Output is: ', output)
print ('Ground Truth Label is: ', label)

score = output [0,label.item()].item() # label对应的class的logits（得分）
print ('Score for the ground truth class = ', label)

first = - score
second = 0
for i in range(5):
    second += math.exp(output[0,i])
second = math.log(second)

loss = first + second
print ('-' * 20)
print ('my loss = ', loss)

loss = nn.CrossEntropyLoss()
print ('pytorch loss = ', loss(output, label))