图像梯度计算
零、梯度理论
可以把图像看成二维离散函数，图像梯度就是这个二维离散函数的求导：
梯度一般产生在边缘位置；
OpenCV 提供了三种不同的梯度滤波器，或者说高通滤波器：Sobel，Scharr和Lapacian。
Sobel，Scharr其实就是求一阶或二阶导。
Scharr是对Sobel的部分优化。
Laplacian是求二阶导。
一、Sobel 算子
一个点附近是什么；
$ G_x 水平, G_y 竖直 $
将附近的点使用权重相加减，得到像素点差异值作为水平/垂直方向的梯度；
以下以 3*3 的核为例
$ G_x = \left[ \begin{matrix} -1 & 0 & +1 \ -2 & 0 & +2 \ -1 & 0 & +1 \end{matrix} \right] * A $
$ G_y = \left[ \begin{matrix} -1 & -2 & -1 \ 0 & 0 & 0 \ +1 & +2 & +1 \end{matrix} \right] * A $
cv2. Sobel 方法
Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]]) -> dst
- ddepth:图像的深度
- dx和dy分别表示水平和竖直方向
- ksize是Sobel算子的大小
import cv2
import numpy as np
import matplotlib.pyplot as plt
lena = cv2.imread('lena.jpg')
lena_gray = cv2.imread('lena.jpg', 0)
pie = cv2.imread('pie.png')
# cv2.CV_64F 的位数更多，能表示负数的形式
sobelx = cv2.Sobel(pie, cv2.CV_64F, 1, 0, ksize=3)
plt.imshow(sobelx)
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
openCV 会对负数做截断；所以上方没有显示右侧的梯度；
解决方法：取绝对值
sobelx = cv2.Sobel(pie, cv2.CV_64F, 1, 0, ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)
plt.imshow(sobelx)
# 将 0，1 参数切换，计算竖直方向，不计算水平方向
sobely = cv2.Sobel(pie, cv2.CV_64F, 0, 1, ksize=3)
sobely = cv2.convertScaleAbs(sobely)
plt.imshow(sobely)
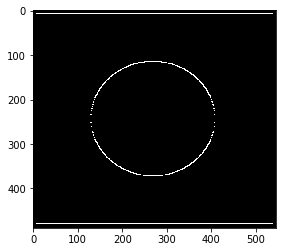
# 不能取 0，0
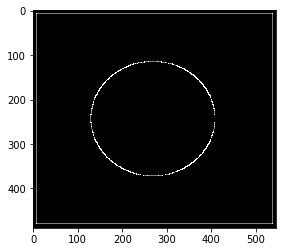
sobelx = cv2.Sobel(pie, cv2.CV_64F, 1, 1, ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)
plt.imshow(sobelx)
# 计算整体的时候，分别计算 x 和 y，再求和；
# 以上都设置为 1 的效果，没有这样求和的效果好；
sobelxy = cv2.addWeighted(sobelx, 0.5, sobely, 0.5, 0)
plt.imshow(sobelxy)
sobelx = cv2.Sobel(lena_gray, cv2.CV_64F, 1, 0, ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)
sobely = cv2.Sobel(lena_gray, cv2.CV_64F, 0, 1, ksize=3)
sobely = cv2.convertScaleAbs(sobely)
sobelxy = cv2.addWeighted(sobelx, 0.5, sobely, 0.5, 0)
plt.imshow(sobelxy)
plt.imshow(np.hstack([lena_gray,sobelxy]))
二、Scharr 算子
Sobel 算子 计算得到的值比较小；对数据更敏感；
$ G_x = \left[ \begin{matrix} -3 & 0 & 3 \ -10 & 0 & 10 \ -3 & 0 & 3 \end{matrix} \right] * A $
$ G_y = \left[ \begin{matrix} -3 & -10 & -3 \ 0 & 0 & 0 \ -3 & -10 & -3 \end{matrix} \right] * A $
scharrx = cv2.Scharr(lena_gray, cv2.CV_64F, 1, 0)
scharry = cv2.Scharr(lena_gray, cv2.CV_64F, 0, 1)
scharrx = cv2.convertScaleAbs(scharrx)
scharry = cv2.convertScaleAbs(scharry)
scharrxy = cv2.addWeighted(scharrx, 0.5, scharry, 0.5, 0)
三、lapkacian 拉普拉斯算子
Laplace Operator
其他算子一般是一阶导；拉普拉斯用到了二阶导；
用中间点和边缘四个点比较；
不建议单独使用；一般和其他算法结合。
$ G = \left[ \begin{matrix} 0 & 1 & 0 \ 1 & -4 & 1 \ 0 & 1 & 0 \end{matrix} \right] * A $
laplacian = cv2.Laplacian(lena_gray, cv2.CV_64F)
laplacian = cv2.convertScaleAbs(laplacian)
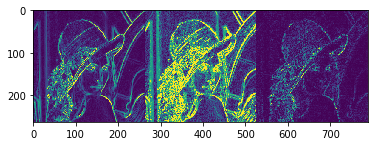
res = np.hstack((sobelxy, scharrxy, laplacian))
plt.imshow(res)
