LSTM 长短时记忆网络

目录

LSTM 长短记忆网络

LSTM 是 RNN 的升级版，应用更广泛。

解决的问题：

增加控制参数C，保留有价值的信息；

C 可以看做一个权重列表：[0, 0.1, 0.8, 1] 舍弃，小部分保留，大部分保留，全部保留。

LSTM 的重点是 控制参数怎么更新

如何训练C参数？

门是一种让信息选择式通过的方法
Sigmoid 神经网络层和一乘法操作

Sigmoid 公式：
$ g(z) = \frac{1}{1 + e^{-z}}$

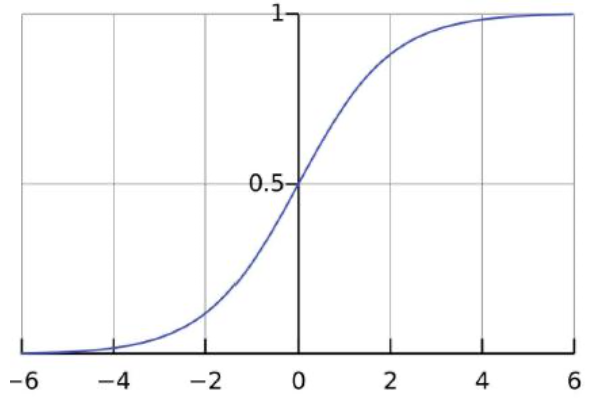
Sigmoid 在负无穷到正无穷的范围类，数值在 0--1 之间；
描述每个部分多少量可以通过，0代表不允许任何量通过，1 代表允许任何量通过。

1、决定丢弃信息

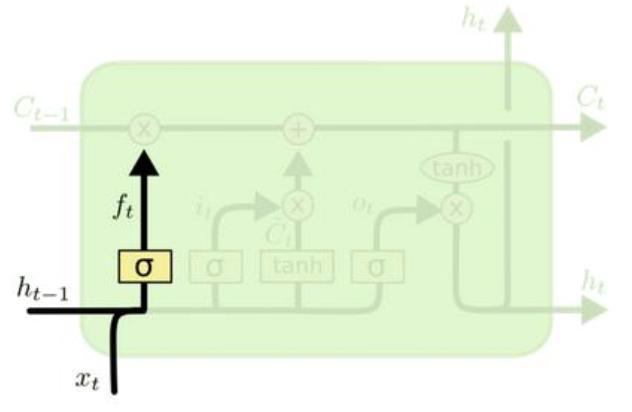
  • \(h_{t-1}\)：上一层中间结果；
  • \(x_t\)：当前数据；
  • \(\sigma\)：激活函数；
  • \(f_t\)：所有值在 0-1 范围之间。\(f_t\) 和 \(C_{t-1}\) 组合，乘法操作，决定丢弃什么信息。

$ f_{t}=\sigma (W_{f} \cdot [h_{t-1}, x_{t} ]+b_{f} )$

2、确定要更新的信息

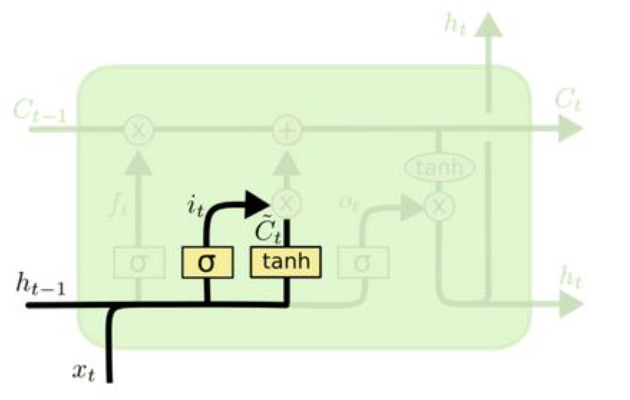
  • \(i_{t}\) 要保留下来的新信息
  • \(C_{t}\) 新数据形成的控制参数

$i_{t} = \sigma (W_{i} \cdot [h_{t-1}, x_{t} ] + b_{i} ) $

\(\tilde{C}_{t} = \tanh (W_{C} \cdot [h_{t-1}, x_{t}]+b_{C} )\)

3、更新细胞状态

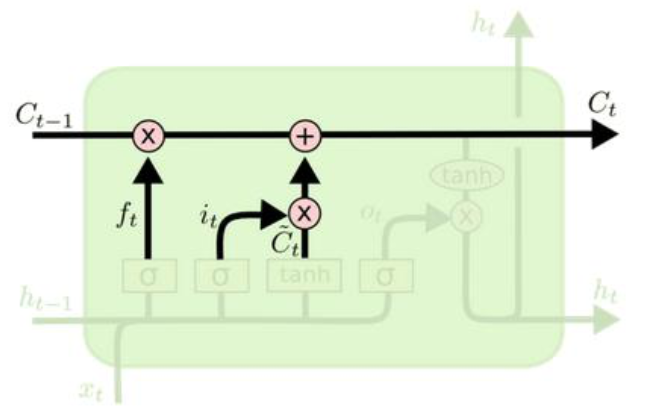
$C_{t} = f_t * C_{t-1} + i_t * \tilde{C}_{t} $

4、输出信息

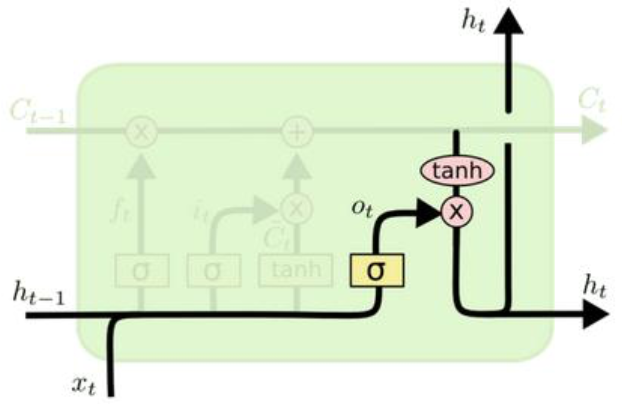
  • \(o_t\)：什么都没忘，全留下的信息
  • \(h_t\)：输出值
  • \(C_t\)：更新完的结果

\(o_t = \sigma (W_o [h_{t-1}, x_t] + b_o)\)

\(h_t = o_t * tanh(C_t)\)

参考资料

posted @ 2021-02-02 08:56  小然-  阅读(98)  评论(0)  编辑  收藏  举报