NN 神经网络
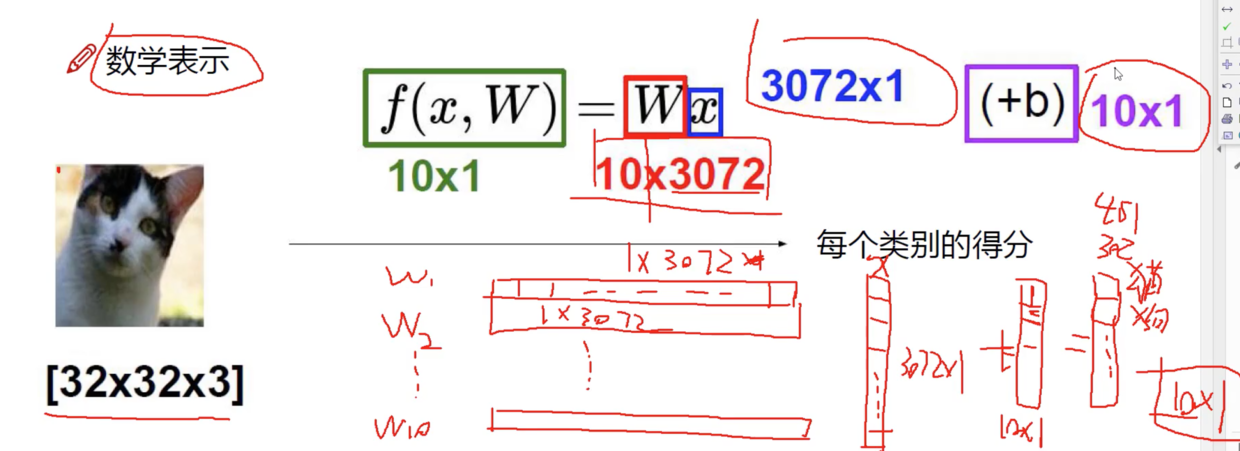
线性函数
也可以称为 得分函数
假设十分类
W 为权重参数,里面每一个数值代表这个点的重要性;正值是促进作用,负数代表抑制作用;控制着决策边界。这里有10 行数据;
b 为偏置,微调;
损失函数
\(L_I = \sum_{j \neq y_i} max(0, s_j - s_{y_i} + 1)\)
神经网络既可以做分类,也可以做回归;
回归任务由得分计算损失,分类任务由概率计算损失。
对于分类问题:
\(s_j\) 其他类别
\(s_{y_i}\) 正确类别
错误类别分数 - 正确类别分数 + 1
\(\delta\) ,代表容忍程度。 在这个式子中,正确类别比错误类别至少高 1 才能看做没有损失; 也可以使用3,5。

计算示例

样本个数
损失函数和样本个数没有关系,在多样本情况下,损失函数表达式为:

损失函数的改进
问题:如果损失函数的值相同,是否意味着两个模型一样?
如下例所示:
$ f(x, W)=W x \(
\) L=\frac{1}{N} \sum_{i=1}^{N} \sum_{j \neq y_{i}} \max(0, f(x_{i} ; W){j}-f(x ; W)_{y_i}+1) $
输入数据: $ x=[1, 1,1,1] \( 模型A:\) w_1 = [1, 0, 0, 0] \( 模型B:\) w_2 = [0.25, 0.25, 0.25, 0.25] $
数据损失:$ w_1^T x = w_2^T x=1$
正则化惩罚项
两个不同的模型 w1 和 w2,得到的结果是一样的,这显然不对;
很明显,模型A只关注局部特征,绝对产生过拟合。
所以构建损失函数的时候,还需要增加 正则化惩罚项。
损失函数 = 数据损失(dataloss) + 正则化惩罚项
\(L=\frac{1}{N} \sum_{i=1}^{N} \sum_{j \neq y_{i}} \max(0, f(x_{i} ; W)_{j}-f(x_{i} ; W)_{y_i}+1) + \lambda R(W)\)
正则化惩罚项:\(R(W) = \sum_k \sum_l W^2_{k,l}\)
神经网络过于强大,容易过拟合。希望模型不要太复杂,过拟合的模型没用。
终极版本:
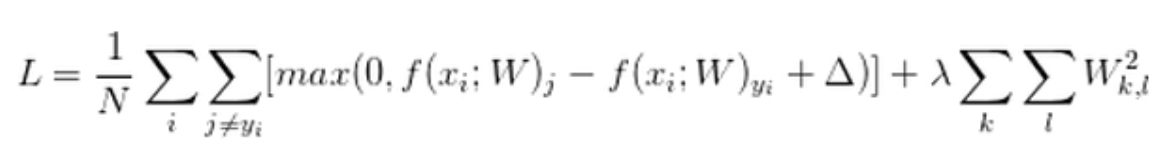
Softmax 分类器
\(s = f(x_i; W)\)
归一化:\(P(Y = k \mid X = x_i) = \frac{e^s k}{\sum_j e^s j}\)
计算损失值: \(L_i=- \log P(Y=y_i \mid X=x_i)\)
计算实例:
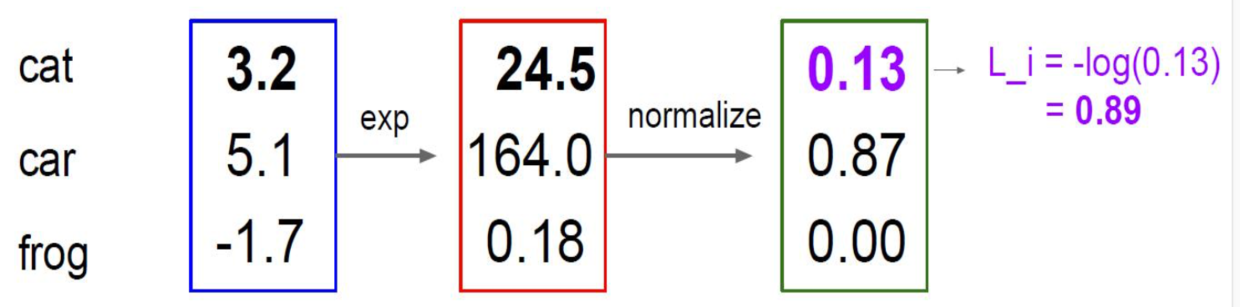
1、使用指数 \(e^3.2 \rightarrow 24.5\)
2、归一化 $ \frac{24.5}{24.5 + 164 + 0.18} \rightarrow 0.13$
3、取对数函数负值 \(L_i = -log(0.13) = 0.89\);正确答案是 cat,所以归一化后的值越接近于 1 越好,取对数越接近于0。
交叉熵损失函数
Cross Entropy Error Function
前向传播 & 反向传播
以上介绍的是前向传播,即知道 x 和 W,到计算完损失。
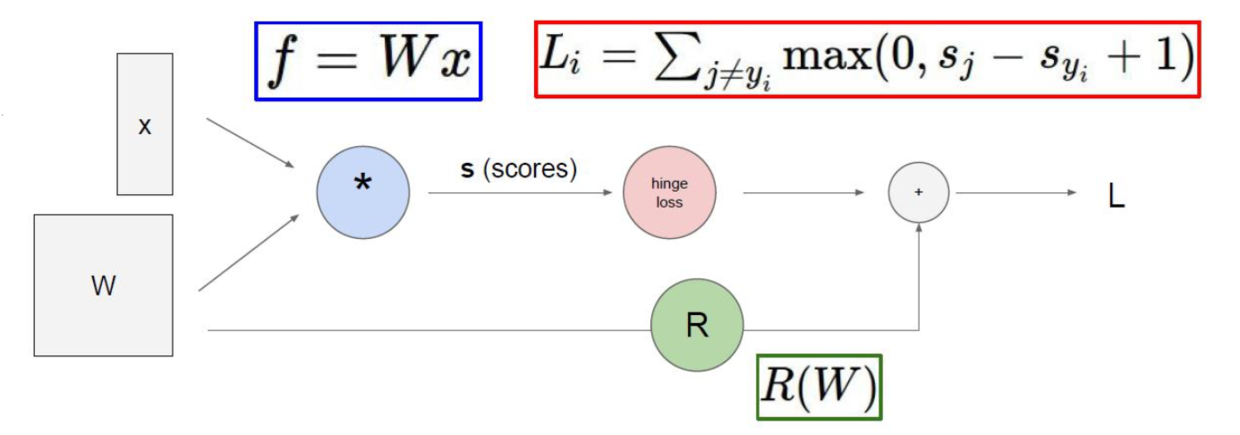
神经网络的目标是:更新、得到最合适的 W。
反向传播:使用梯度下降优化算法,
线性回归中虽然可以求得最终结果,但这个结果只能看做巧合。因为所有机器学习问题中,除了线性回归,其他问题是求解不出最终的真实答案。所以应该想优化思路,来让机器真正学习起来。
机器学习常规套路:给定数据和结果,让机器沿着 loss 减少的方向去做。
反向传播
示例
结果计算: \(f(x, y, z) = (x + y) z\)
期望得到最小的 f 值
want : $ \frac{\alpha f}{\alpha x} , \frac{\alpha f}{\alpha y} , \frac{\alpha f}{\alpha z} $
假设 $ q = x + y$
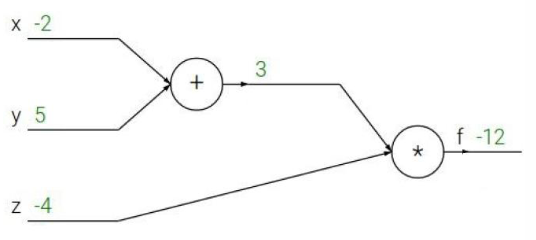
对 x 求偏导: $ \frac{\alpha f}{\alpha x} = \frac{\alpha f}{\alpha q} \frac{\alpha q}{\alpha x}$
对 y 求偏导: $ \frac{\alpha f}{\alpha y} = \frac{\alpha f}{\alpha q} \frac{\alpha q}{\alpha y}$
链式法则
梯度是一步步传播的
正向传播中$ [(xw_1) w_2 ] w_3 = f $
反向传播,要从后往前,逐层求这一层的影响(求导)
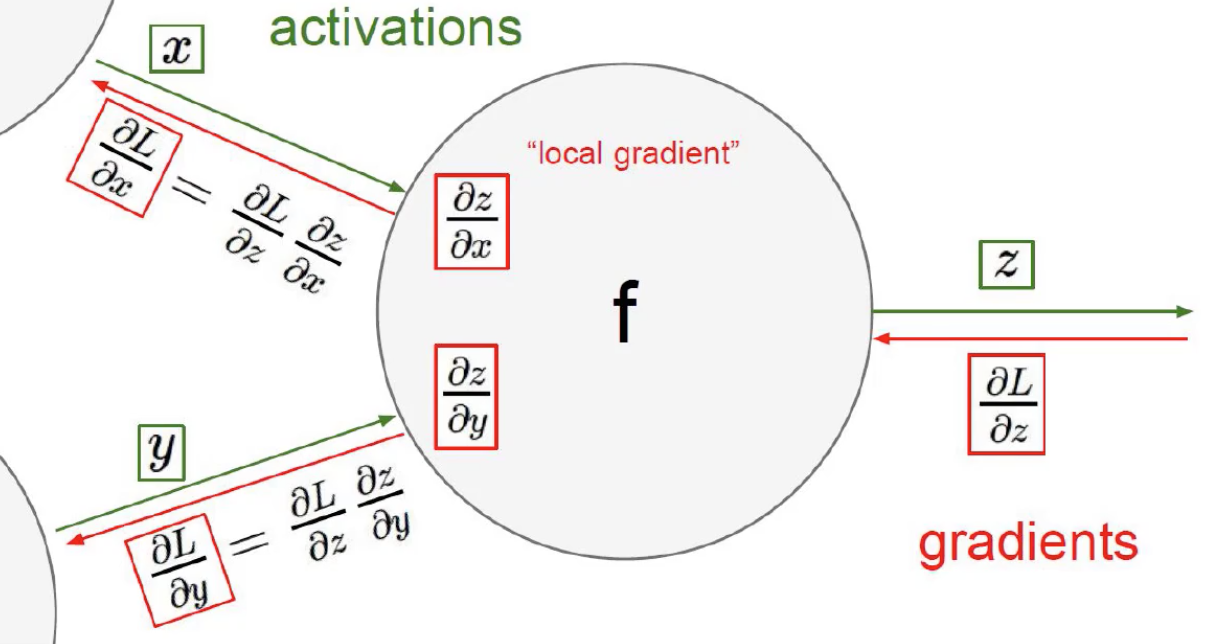
实际情况不是求数据的偏导,而是求 矩阵 的偏导。拿笔计算不现实。
不止可以一步步计算,也可以整体大块计算,作为 sigmoid gate。
门单元
- 加法门单元:均等分配
- MAX 门单元:给最大的
- 乘法门单元:互换的感觉
其实跟生物学没有关系,只要知道数学模型、权重、矩阵参数的计算过程即可。
神经网络的根本工作,就是找权重参数:什么样的权重参数,最适合当前的任务。
整体架构
- 层次结构
- 神经元
- 全连接
- 非线性:每一步矩阵计算之后
隐藏层的数据,不一定有实际意义,只是对于计算机更容易分辨。
基本结构
\(f = W_2 max(0, W_1x)\)
继续堆叠一层
\(f = W_3 max(0, W_2 max(0, W_1x))\)
神经网络的强大之处在于,用更多的参数来你和复杂的数据。
通常情况是 千万到上亿的参数。
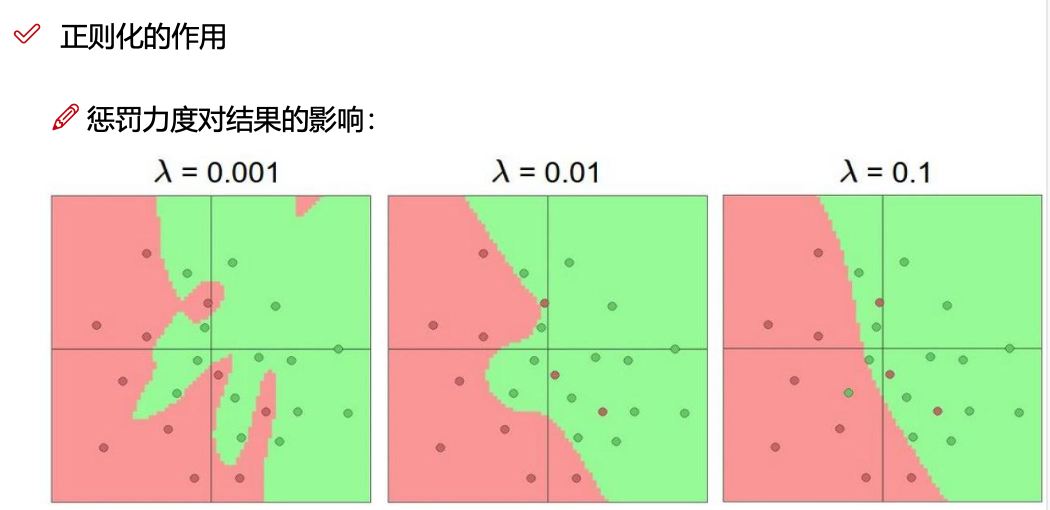
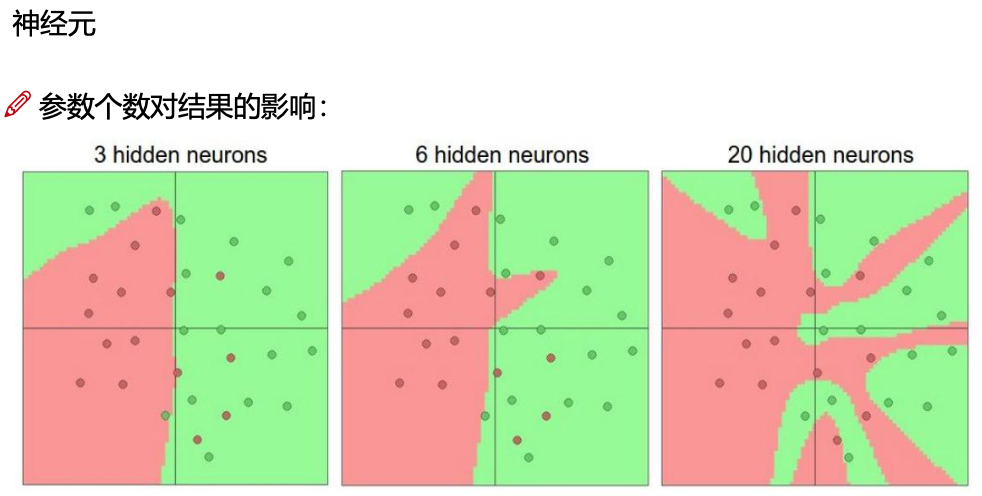
神经元越多,过拟合风险越大
激活函数
使用函数 Sigmoid,Relu,Yanh 等

最早神经网络就是使用 Sigmoid 来做,现在基本不用了。因为一旦数值较大或较小,得到的结果就不好了,会出现梯度消失现象。(函数图像两端趋向平稳,求导为0)
现阶段更多使用 Relu 函数或 Relu 函数的变体。

数据预处理
1、标准化
一般会做 标准化操作:中心化(减均值),放缩扩充(除标准差)
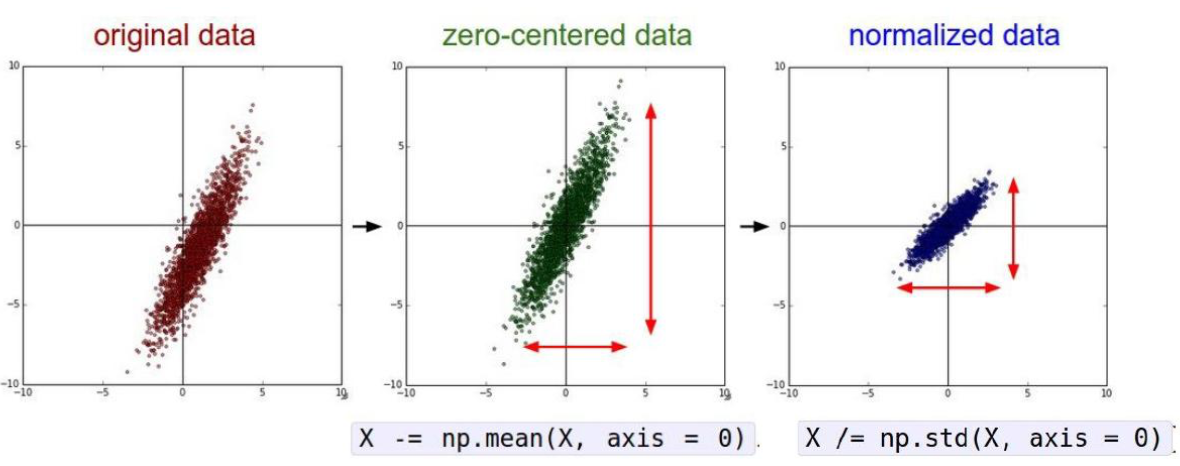
2、初始化
通常使用随机策略 来进行参数初始化;
不让网络中不同的权重参数值W浮动太大;
$ W = 0.01 * np.random.randn(D, H)$
其他
文本去停用词,图像数据标准化等
解决过拟合问题
一般会加正则化 RW 让神经网络不要太强;
也可以使用Drop-out 来消减网络威力。
是传说中的 七伤拳:伤敌七分,自损三分。
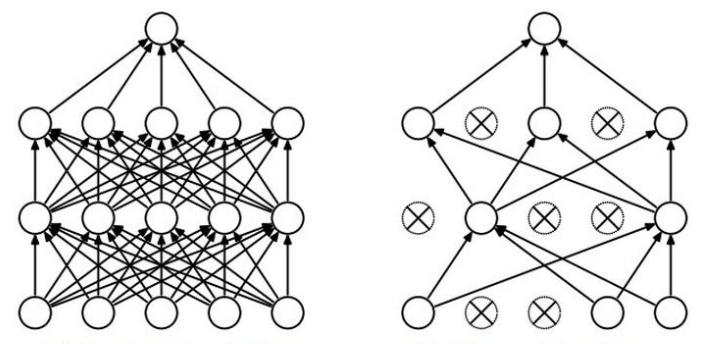
左图为全连接网络;
在神经网络训练阶段,按照比例 随机杀死一部分神经元(这次迭代不使用,下次可能使用)。在测试阶段,没必要杀死,会拿整个神经网络来直接进行测试。
神经元个数对结果的影响
理论情况下,神经元越多,过拟合的风险越大。速度更慢。
一般 64,128 是常见的值。
可视化展示的神经网络:
https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html
- Mr.括号:神经网络15分钟入门!足够通俗易懂了吧
https://zhuanlan.zhihu.com/p/65472471



 浙公网安备 33010602011771号
浙公网安备 33010602011771号