不失一般性和快捷性地判定决策单调（洛谷P1912 [NOI2009]诗人小G）（动态规划，决策单调性，单调队列）
闲话
看完洛谷larryzhong巨佬的题解，蒟蒻一脸懵逼
如果哪年NOI（放心我这样的蒟蒻是去不了的）又来个决策单调性优化DP，那蒟蒻是不是会看都看不出来直接爆\(0\)？！
还是要想点办法，不失一般性也能快捷地判定决策单调。
对于判定决策单调的分析
再补一句决策单调性的概念：状态转移方程形如\(f_i=\min/\max_{j=1}^{i-1} g_j+w_{i,j}\)，且记\(f_i\)的最优决策点为\(p_i\)（也就是\(f_i\)从\(g_{p_i}+w_{i,p_i}\)处转移最优）若满足\(p_i\le p_{i+1}\)，则该方程满足决策单调性。（摘自蒟蒻的DP优化总结）
显然每个决策\(j\)可以用一个关于\(i\)的函数\(f_j(i)\)表示。
函数的一个重要思想：数形结合！
光靠脑子想不到规律，只好先举一些用语言难以描述的反例。我们的函数不能这样
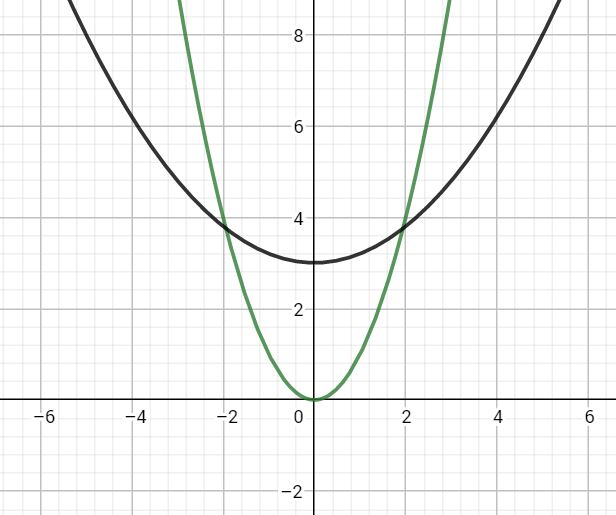
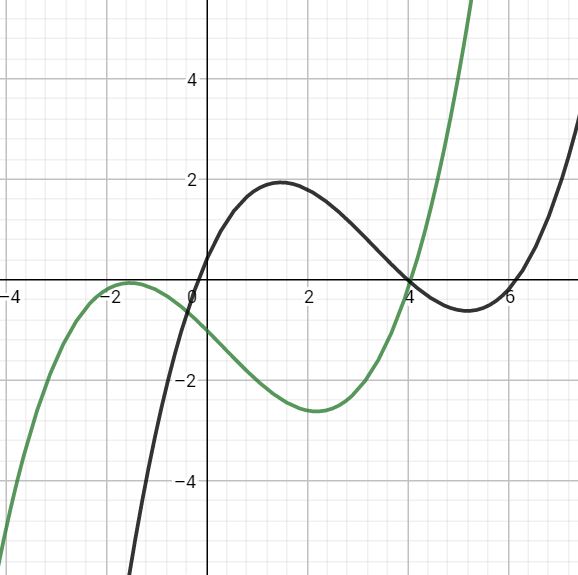
看到这里Dalao们有没有一点想法呢？蒟蒻反正想到了一点——两个函数必须只有一个交点！在这一点之前一个函数更优，而之后就被永远取代了。
感觉满足条件的函数其实很少，分类讨论一下（如有误欢迎Dalao指教）
直线
显然上面的基本要求都满足。不过要是函数是直线的话都可以用斜率优化搞了（\(k_1x+b_1\ge k_2x+b_2,x\ge\frac{b_2-b_1}{k_1-k_2}\)）。
不是直线
为了避免图1的尴尬情况，可能需要所有决策函数之间可以通过平移相互变换（形如\(f_j(x)=f_k(x-a)+b\)）。
为了避免图2的尴尬情况，可能需要函数的导函数在各自的定义域内单调递增/递减（注意是导函数不是原函数）。
接着，根据蒟蒻肝过的几个题，好像还有一条规律——
如果导函数递增、求最大值（柠檬），或者导函数递减、求最小值，要用单调栈。
如果导函数递增、求最小值（本题），或者导函数递减、求最大值（Lightning Conductor），要用单调队列。
复杂的函数
蒟蒻见过这一道（Yet another minimization problem）
感觉可以看成对于每一种数都有一个函数\(\frac{(c_i-c_j)(c_i-c_j+1)}{2}\)，单看这一个是满足决策单调性的（\(c_i\ge c_j\)，定义域内的导函数是递增的）。
那么总函数就可以写成\(f_j(i)=g_j+\sum\frac{(c_i-c_j)(c_i-c_j+1)}{2}\)，怎么看也不像是不满足决策单调性的。
本题的思路
那么就可以回归本题了。
设\(len_i\)为第\(i\)句的长度，\(s_i=i+\sum\limits_{j=1}^i len_j\)（加上\(i\)是默认一句话后面有空格）
设\(f_i\)为选前\(i\)句的最小代价，我们枚举当前这一行填入最后面的多少个句子，注意行末没有空格，长度要\(-1\)，那么有方程
容易发现后面这一坨决策函数是关于直线\(x=s_j+1+L\)对称的。把它去绝对值，变成两段，显然左边一段和右边一段的导函数都是递增的，左边恒\(<0\)，右边恒\(>0\)。又因为这函数是连续的，所以当然整个函数的导函数也单调递增咯！
用队列维护决策二分栈的过程不再赘述，总结里也有。时间复杂度\(O(Tn\log n)\)
看到Dalao们都记录了一个三元组，可蒟蒻还是觉得没啥必要啊。。。只要保存队列中相邻两个元素的临界值\(k\)就好了吧。
一个写法技巧：
二分决策\(x,y(x<y)\)的临界值的时候，左端点设成\(x\)就好了，没必要设成\(1\)（难怪蒟蒻之前写Lightning Conductor跑得有点慢）
三个坑点：
不管是转移还是输出，都要去掉行末的空格（怪蒟蒻看题不清）
当答案大于\(10^{18}\)的时候开longlong也炸了，所以要用实数以牺牲精度的代价换来更大的值域。然而double真的WA了。于是要开long double。
cmath的pow太慢了容易TLE，要手写快速幂。
#include<cstdio>
#include<cmath>
#include<cstring>
#define RG register
#define R RG int
#define G c=getchar()
#define Calc(i,j) f[j]+qpow(abs(s[i]-s[j]-L))//计算函数值
using namespace std;
typedef long double LD;//开long double
const int N=1e5+9;
int n,L,P,s[N],q[N],k[N],pr[N];
LD f[N];
char str[N][33];
inline int in(){
RG char G;
while(c<'-')G;
R x=c&15;G;
while(c>'-')x*=10,x+=c&15,G;
return x;
}
inline LD qpow(RG LD b){//自己写快速幂
RG LD a=1;
for(R k=P;k;k>>=1,b*=b)
if(k&1)a*=b;
return a;
}
inline int bound(R x,R y){//二分临界值
R l=x,r=n+1,m;//左端点设为x减小常数
while(l<r){
m=(l+r)>>1;
Calc(m,x)>=Calc(m,y)?r=m:l=m+1;
}
return l;
}
int main(){
R T=in(),i,h,t;
while(T--){
n=in();L=in()+1;P=in();//把L处理了一下
for(i=1;i<=n;++i){
if(scanf("%s",str[i]));
s[i]=s[i-1]+strlen(str[i])+1;//记前缀和
}
for(q[i=h=t=1]=0;i<=n;++i){
while(h<t&&k[h]<=i)++h;
f[i]=Calc(i,q[h]);pr[i]=q[h];//记录转移位置方便输出方案
while(h<t&&k[t-1]>=bound(q[t],i))--t;
k[t]=bound(q[t],i);q[++t]=i;
}
if(f[n]>1e18)puts("Too hard to arrange");
else{
printf("%.0Lf\n",f[n]);
for(q[t=0]=i=n;i;q[++t]=i=pr[i]);
for(;t;--t){
for(i=q[t]+1;i<q[t-1];++i)
printf("%s ",str[i]);
puts(str[i]);//行末不要搞空格
}
}
puts("--------------------");
}
return 0;
}
