TSP的一个确定性多项式时间近似算法(环覆盖,图匹配,最小生成树,概率统计分析)
问题描述
给定一个图,求出一个不重复遍历所有点的环路,使环路的边权之和最小
TSP(旅行商问题)是一个著名的NP-Hard问题,无法在任意情况下使用多项式时间算法精确求解
根据给定图的性质,我们可以对问题做一些细分类
-
图是有向图还是无向图
-
图是否为完全图(实际上,非完全图可以通过将不存在边的边权视为INF,转化为完全图)
-
图的边权是否满足度量性质(metric)
或称是否满足三角不等式,\(\forall x, d(u,v)\le d(u,x)+d(x,v)\)
TSP在实际应用背景下,许多情况都满足此性质
比如点在几何空间中,所有边权为两点距离
又比如点在地图上,所有边权为两点之间最短路(尽管路径上可能有别的点)- 研究指出,对于metric情况,存在常数级多项式时间近似算法(即该算法所求结果与最优解比值小于某个常数)
比如求出图的最小生成树,将其的一个dfs序作为环,可以证明得到近似比小于\(2\)的解
比如Christofides算法的近似比为\(\frac32\) - 研究也指出,对于non-metric情况,不存在普遍的常数级多项式时间近似算法
- 研究指出,对于metric情况,存在常数级多项式时间近似算法(即该算法所求结果与最优解比值小于某个常数)
算法概述
通过求解图的最小环覆盖,再将所有环以一定的方式合并成一个环,即得到一个解
最小环覆盖(vertex cycle cover)
https://en.wikipedia.org/wiki/Vertex_cycle_cover
在给定图中,选出任意个环路,使它们互不相交且正好覆盖所有点,最小化边权总和
显然对于同一个图,最小环覆盖的答案一定不大于TSP问题的答案,因为TSP所求的一个环路也是合法的环覆盖
那么最终的近似程度就很大程度取决于合并所有环带来的代价
至于如何求解,我们对有向图和无向图分别讨论
有向图
每个点都恰好有一条出边和一条入边,这是构成不相交环的充要条件
于是问题转化为二分图最小权完美匹配问题
二分图两边各\(n\)个点,对于原图中的每条边\((u,v,w)\),在二分图中把左边的\(u\)和右边的\(v\)连起来
使用KM算法,复杂度\(O(n^3)\)
无向图
不好套用有向图的做法,因为允许了\(u\to v\to u\)这样的二元环存在
主要后果并不是违反了无向图环的定义,而是大大提高了合并环的代价
试想一个图中的那些权值特别小的边,很倾向于形成二元环,那么最终最小环覆盖环的个数就会爆炸
怎么办呢?来点概念
reference: https://cstheory.stackexchange.com/questions/46819/algorithm-for-finding-a-3-cycle-cover
https://mathoverflow.net/questions/277498/tuttes-reduction-of-minimum-weight-d-factors-to-matching
-
d-regular, spanning subgraphs (d-factors)
正则生成子图,指的是某图的一个包含原图所有点的子图,满足每个点的度数均为\(d\)
比如完美匹配等价于1-factor,环覆盖等价于2-factor -
Tutte's Reduction
由Tutte提出,将d-factor求解转化为图匹配求解
对于原图每个点\(u\),新建点\(u_1,...,u_d\)
对于原图每条边\(e:(u,v,w)\),新建点\(e_u,e_v\),新建边\((e_u,e_v,w)\)
并且\(\forall i\in[1,d]\),新建边\((u_i,e_u,0),(v_i,e_v,0)\)
求出该图的最大权完美匹配
对于新图的\((e_u,e_v,w)\)型边,它在匹配边中当且仅当对应原图边\(e\)未被选入最小环覆盖
对于新图的\((u_i,e_u,0)\)型边,它在匹配边中当且仅当对应原图边\(e\)被选入最小环覆盖
为什么这样是对的呢?显然新图存在完美匹配,那么既然新图的\(u_i,e_u\)已经匹配,\(e_v\)就肯定会和\(v_j\)匹配,不会自相矛盾
那么最大化匹配边的权值和,就是最小化d-factor的权值和
例如对于三个点的最小环覆盖,建新图
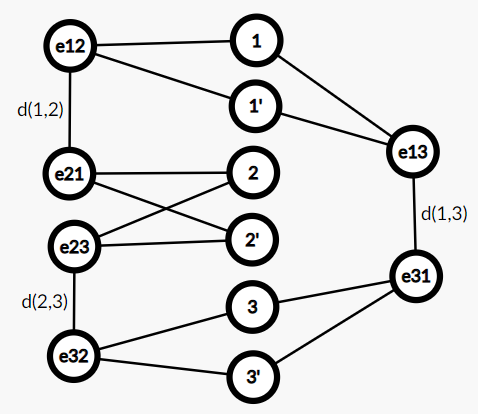
显然完美匹配中\((e_u,e_v,w)\)型边一个都不能选,原图也只有唯一环覆盖
可是这是个一般图呀,最大权完美匹配怎么做?
OI中相对普及的是二分图最大权完美匹配的KM算法、一般图最大匹配的带花树算法
一般图最大权完美匹配算法(Maximum Weight Perfect Matching)由Edmonds提出,实际上就是上述两种思想的结合
但其理解和实现的难度就不是两个算法的简单相加了TAT
需要学习的大佬可以参考洛谷P6699 【模板】一般图最大权匹配,UOJ#81. 一般图最大权匹配
注意最大权匹配和最大权完美匹配是不一样的
目前普遍的\(O(n^3)\)实现方法,代码量基本都是7k左右
广为流传的Min_25大佬的\(O(nm\log n)\)实现,代码量已经到了20多k!!!

还好可以从现成的算法库里调用,比如Python的networkx,C++的LEMON图论库
对于最小环覆盖,两种实现的复杂度分别为\(O(m^3),O(m^2\log n)\)(\(n,m\)为原图点数,边数)
环的合并
每次挑两个环出来,枚举断开的位置和接的方向,合成一个环
至于挑环的顺序,又可以搞好多方法出来
大环优先法
蒟蒻的想法,每次把次大的环往最大的环上合
这样做是为了让最小的环能在其合并时枚举到尽可能多连接的方式(小环长度×大环长度×2)
假如两个小环合并,连接方式很少,最优方式的代价期望就会提大大高
类MST kruscal法
也是蒟蒻的想法,每次选择所有环对中的一个最优方式进行合并
我们把环看成一个超级点,把合并看成两个超级点连边,就类比到了MST上
这是靠几何直觉大致表明这种方法在metric情况下makes sense
而且这样做也大概率比大环优先法优秀,这个贪心只是忽略了先合并的环有两条边被删掉的轻微后效性
逐次缩环法
论文算法(Cycle Shrinking Algorithm),但是需要允许构造经过某些点多次的路径,适合贴近现实的metric情况
每次求出最小环覆盖后,若环数为1,停止
否则从每个环中选择一个代表点,构造新图,新图中两点之间边权为原图中两点最短路
再求新图的最小环覆盖,如此循环
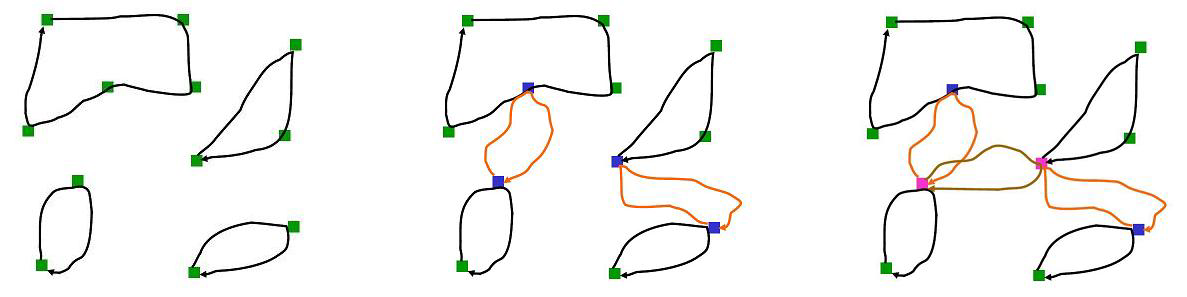
因为每次建新图,点数比原来至少少一半,所以最多执行\(O(\log n)\)次最小环覆盖
又因为每次最小环覆盖长度不超过TSP的答案,所以该算法被证明有\(O(\log n)\)的近似比
部分情况下该算法的近似程度分析以及改进探讨
有向完全图,所有边权随机
这里每一条边都是i.i.d.的连续型随机变量
运行算法,我们得到一个匹配,可以视为一个全错位的置换\(\pi\),左边点\(u\)匹配到右边点\(\pi(u)\)
我们关心环的个数的期望,也就是\(\pi\)中循环的个数的期望
有一个结论:得到所有合法置换的概率是相等的,因为所有边是i.i.d.的,得到任意两个置换的概率都可以通过点、边的映射相互转化,用对称性证明它们相等
因此我们直接求等概率随机一个长度为\(n\)全错位排列的循环个数期望\(L_n\)
- A008306:\(T(n,k)\)为\(n\)元素划分成\(k\)个长度至少为\(2\)的圆排列的方案数,又称连带第一类Stirling数
- A000166:\(D_n\)为全错位排列数
- A162973:\(\sum_{k=1}^{n/2}kT(n,k)\)
它是\(\log n\)级别的!也就是说,合并环所带来的长度增加是非常有限的,近似解和最优解的绝对误差大概率在一个合理的范围内
无向完全图,所有边权随机
A038205:\(n\)元素划分成个长度至少为\(3\)的圆排列的方案数
然并卵,不能像有向图中那样用对称性了,只能说明同构的环覆盖概率相等,于是蒟蒻不会算期望了/kk
不过既然环长至少为\(3\)了,那么环数期望肯定不超过有向图的情况\(O(\log n)\)
通过重复随机采样,能说明
- 得到更大环长、更少环数的环覆盖的概率更高
- 环数期望似乎与概率分布也有关?
算法变种
我们另一个关心的是\(O(m^2\log n)\)的复杂度,在跑上百个点的完全图的时候就开始吃力了
不过既然不是确定出正解的算法了,想怎么乱来都行,能降一点复杂度,快点跑出来就好
通过观察,我们发现,实际上在点很多、图很密集的情况下,那些边权稍微大一点的边都基本上用不上了
假如我们知道最大的能被用上的边的边权\(W\),我们只留下边权不超过\(W\)的边(条数为\(c\))建新图跑MWPM,新图的点数和边数就会减少到\(O(n+c)\)
比如,\(n=100,d(u,v)\sim\operatorname{Unif(0,1)}\)时,把大于\(0.1\)的边都删掉,能变快将近一百倍
-
蒟蒻找到了论文中的一个定理,给了这个胡搞一定的理论依据
假设常数\(K>16,p\ge\frac{K\log n}{n}\),那么在\(n\)个点的完全图中让每条边以概率\(p\)出现,\(1-p\)不出现,
这个图存在Hamilton回路是高概率事件(\(n\to\infty,P(·)\to1\))那也就是说,我们需要在原图留下\(\Omega(n\log n)\)的边来保障我们高概率找到一个环覆盖
基于这个依据还需要一个猜测,那就是加入边权更大的边对最小环覆盖的改善很微小
假设这些都是对的,那令\(c=O(n\log n)\),我们用\(O((n+c)^2\log n)=O(n^2\log^3 n)\)的时间能高概率找到一个很小的环覆盖
关键是不知道\(W\)是多少
一种方法是自己生成几组数据多试试,再把\(W\)定下来
另一种方法是交给算法把它试出来,采用倍增试探法
- 令\(c=n\)
- 留下前\(c\)小的边,建新图跑一般图完美匹配(甚至能上随机算法,跑得快并且大概率对就行)
- 如果成功找到完美匹配,令\(W=\)第\(c\)小边的边权,结束;否则\(c=2c\),转步骤2.
无向图,metric,二维平面点
这里仅与Christofides算法作对比
通过重复随机采样(在矩形区域中随机选择整数点),该算法有80%的概率优于Christofides算法
以下的两个例子,能够很好的说明问题
例子一
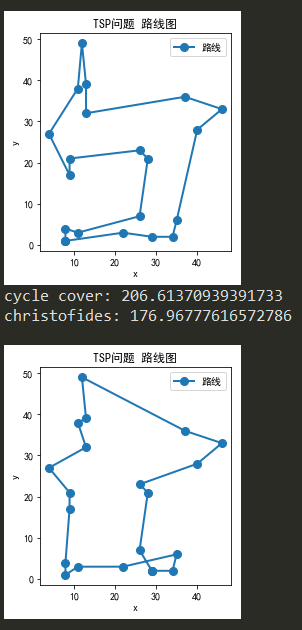
Christofides更优秀,该算法形成的解被已形成的几个小环大大限制住了,陷入了局部最优
目测来看,可以基于对解进行点交换、部分环交换等局部调整的方法,应用贪心或者模拟退火的算法,将当前情况大大改善
另一方面,找到更可靠的环合并算法也是非常有希望的研究方向
例子二

该算法更优秀,Christofides的解出现了许多交叉的地方
这是因为最小环覆盖在二维平面下的性质:不存在两个环相交

比如这种情况,显然把两个交叉的地方打开,重新分配环\((a_1,b_2,b_3,a_4),(b_1,a_2,a_3,b_4)\)一定更优
然而合并环后仍有极小概率出现交叉,问题还是陷入局部最优,比如下面,左边是该算法,右边是真正最优解

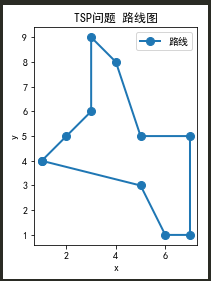
解决最终解交叉的方法,就是直接枚举检查每两条边是否相交,相交了就打开,一定有一种调整方式使得调整后仍然是Hamilton回路
这样一来Christofides的解也能大大改善,也就不能说该算法大概率比Christofides好了
Python实现一例
无向完全图,边权为\(\text{Beta}(0.5,0.5)\)分布,输入文件格式为邻接矩阵
这个是大环优先法的实现
import networkx as nx
# 读入数据处理
with open("input.txt","r") as f:
finput = f.readlines()
d = [[0] + list(map(int, fline.split())) for fline in finput]
n = d[0][1]
W = 0.1 # 上面算法改进提到的边权限制
# MWPM建图
G = nx.Graph()
G.add_nodes_from(range(-n, 0))
G.add_nodes_from(range(1, n+1))
for u in range(1, n+1):
for v in range(u+1, n+1):
if d[u][v] > W: continue
G.add_node((u,v))
G.add_node((v,u))
G.add_edge((u,v), (v,u), weight=d[u][v])
G.add_edge( u, (u,v), weight=0)
G.add_edge(-u, (u,v), weight=0)
G.add_edge( v, (v,u), weight=0)
G.add_edge(-v, (v,u), weight=0)
match = nx.algorithms.max_weight_matching(G, maxcardinality=True)
# 将匹配结果处理为环覆盖形式
w = 0
w_max = 0
w_ignore = 0
H = nx.Graph()
for e in match:
if type(e[0])==int:
u, v = e[1]
elif type(e[1])==int:
u, v = e[0]
else:
w_ignore += d[e[0][0]][e[0][1]]
continue
if u < v:
w += d[u][v]
w_max = max(w_max, d[u][v])
H.add_edge(u,v)
cycle = nx.algorithms.cycle_basis(H)
print("w=", w, "c=", len(cycle), cycle)
print("w_max=", w_max)
# 合并环
while len(cycle) > 1:
merge = None
mdelta = float("inf")
for id1,c1 in enumerate(cycle):
for id2,c2 in enumerate(cycle):
if id1 >= id2:
continue
for i in range(len(c1)):
for j in range(len(c2)):
u, v = c1[i], c1[(i+1) % len(c1)];
x, y = c2[j], c2[(j+1) % len(c2)];
delta = d[u][x] + d[v][y] - d[u][v] - d[x][y]
if mdelta > delta:
mdelta = delta
merge = (id1, id2, c1[:i+1]+c2[j::-1]+c2[:j:-1]+c1[i+1:])
delta = d[u][y] + d[v][x] - d[u][v] - d[y][x]
if mdelta > delta:
mdelta = delta
merge = (id1, id2, c1[:i+1]+c2[j+1:]+c2[:j+1]+c1[i+1:])
cycle.pop(merge[1])
cycle.pop(merge[0])
cycle.append(merge[2])
# 输出答案
ans = cycle[0]
if n != len(ans):
raise Exception("not connected!")
w = 0
for i in range(len(ans)):
w += d[ans[i]][ans[(i+1) % len(ans)]]
print("w=", w, ans)
总结
该算法非常适合non-metric,边权独立随机,图点数中等的情况
该算法在metric情况下适用性不高,因为解的近似性不如Christofides稳定,时间复杂度高(Christofides为\(O(n^3)\))
这也是在意料之中的,因为metric情况下,形成局部小环的概率提高,环数期望增加,也没有完全利用三角不等式的性质


 浙公网安备 33010602011771号
浙公网安备 33010602011771号