一个小问题引发的惨案(计算几何,Voronoi图,半平面交,分治)
某天无聊,脑子里突然蹦出一个小问题:
给定一个矩形平面,有\(n\)个相同功率的通信基站,请在平面上求出信号最弱的位置
或者说,有\(n\)个点,找出一个位置,使其离这些点中最近的点最远
是不是一个很简单的小问题呢
引入Voronoi图,定义法
对于平面上每个位置,都能找到离其距离最近的一个点。反过来看,每个点都对应一个离它距离最近的位置集合。
我们需要求的答案位置,必是\(n\)个集合中离点最远的位置中最远的那一个
这个集合长啥样呢?
对于点\(i\),枚举点\(j(1\le j\le n,i\ne j)\),平面上到\(i\)比到\(j\)近的部分,是两点中垂线分割开、靠\(i\)近的一侧半平面
那么平面上到\(i\)比到其它点都近的部分,就是\(n-1\)个半平面与矩形的交,会是一个多边形,点\(i\)称为该多边形的基点
把所有\(n\)个多边形求出来,它就有了专业名称:Voronoi图,多边形称为泰森多边形(百度百科)

多边形的集合是整个平面的一个划分,这样的定义赋予了泰森多边形深刻的现实意义:假设设备都连到距离最近的基站上,那么每个多边形就是对应基站的服务区域
类似地,在地理学、天文学、结晶化学、城市规划等方面也有着切实的应用
至此我们也给出了构建Voronoi图的朴素算法:定义法,求\(n\)个半平面交,复杂度\(O(n^2\log n)\)
半平面交算法可参考蒟蒻的计算几何细节梳理&模板
//n=2000,time=1800ms
#include<cstdio>
#include<cmath>
#include<iostream>
#include<iomanip>
#include<algorithm>
#define double long double
#define TEST
using namespace std;
const int N=2009;
const double PI=acos(-1),EPS=1e-10;
struct Point{
double x,y;
Point(){x=y=0;}
Point(double a){x=a;y=0;}
Point(double a,double b){x=a;y=b;}
friend istream&operator>>(istream&is,Point&a){return is>>a.x>>a.y;}
friend ostream&operator<<(ostream&os,Point a){return os<<a.x<<','<<a.y;}
Point operator-(){return Point(-x,-y);}
Point operator+(Point a){return Point(x+a.x,y+a.y);}
Point operator-(Point a){return Point(x-a.x,y-a.y);}
Point operator*(double a){return Point(x*a,y*a);}
Point operator/(double a){return Point(x/a,y/a);}
friend Point operator*(double a,Point b){b.x*=a,b.y*=a;return b;}
Point&operator+=(Point a){x+=a.x,y+=a.y;return*this;}
Point&operator-=(Point a){x-=a.x,y-=a.y;return*this;}
Point&operator*=(double a){x*=a,y*=a;return*this;}
Point&operator/=(double a){x/=a,y/=a;return*this;}
double operator*(Point a){return x*a.x+y*a.y;}
double operator%(Point a){return x*a.y-y*a.x;}
double Len(){return sqrt(x*x+y*y);}
friend double Dis(Point a,Point b){return (a-b).Len();}
Point Turn90(){return Point(-y,x);}
}a[N];
struct Line{
Point p,v;double ang;
Line(){}
Line(Point a,Point b){p=a,v=b-a,ang=atan2(v.y,v.x);}
friend ostream&operator<<(ostream&os,Line a){return os<<a.p<<' '<<a.v;}
bool operator<(Line&a){return ang<a.ang;}
bool Right(Point&a){return v%(a-p)<EPS;}
friend Point Cross(Line a,Line b){return a.p+a.v*(b.v%(b.p-a.p))/(b.v%a.v);}
}l[N];
int n,w,h;
Line q[N],*qq;
Point k[N],*kk;
int HalfPlane(Line*a,int n){//半平面交
int h=0,t=0;
sort(a,a+n);
q[0]=a[0];
for(int i=1;i<n;++i){
while(h<t&&a[i].Right(k[t-1]))--t;
while(h<t&&a[i].Right(k[h]))++h;
if(fabs(q[t].ang-a[i].ang)>EPS)q[++t]=a[i];
else if(a[i].Right(q[t].p))q[t]=a[i];
if(h<t)k[t-1]=Cross(q[t-1],q[t]);
}
while(h<t&&q[h].Right(k[t-1]))--t;
k[t]=Cross(q[h],q[t]);
qq=q+h;
kk=k+h;
return t-h+1;
}
int main(){
freopen("in.in","r",stdin);
freopen("halfplane.out","w",stdout);
cin>>n>>w>>h;
for(int i=1;i<=n;++i)
cin>>a[i];
double ans=0;
for(int i=1;i<=n;++i){
int m=0;
for(int j=1;j<=n;++j)
if(i!=j){
Point mid=(a[i]+a[j])/2,v=a[j]-a[i];
l[m++]=Line(mid,mid+v.Turn90());
}
l[m++]=Line(Point(0,0),Point(w,0));
l[m++]=Line(Point(w,0),Point(w,h));
l[m++]=Line(Point(w,h),Point(0,h));
l[m++]=Line(Point(0,h),Point(0,0));
m=HalfPlane(l,m);
#ifdef TEST//测试生成多边形的边数,检查是否成功处理退化情况
cout<<m<<endl;
#endif
for(int j=0;j<m;++j)
ans=max(ans,Dis(a[i],kk[j]));
}
cout<<ans<<endl;
return 0;
}
引入Delaunay三角网,逐点插入法
Voronoi图是平面图,Delaunay三角网与它互为对偶图(对于Voronoi图的每条边,连接其相邻两个泰森多边形的基点)
这两者联系起来,有着许多奇妙的数学性质,这里只略提一二,方便后面算法的引入
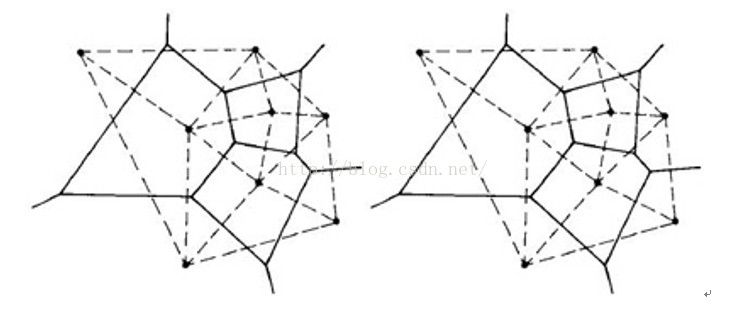
一般情况下,Voronoi图的每个顶点与三条边相连,在Delaunay三角网中,周围的三个基点连成三角形,顶点是这个三角形的外接圆圆心(中垂线交点)
(暂不讨论特殊情况:多个基点共圆,Voronoi图的每个顶点与更多边相连,多个Delaunay三角形外接圆圆心重合)
由此引入Delaunay三角网的重要性质:对于其中任意一个三角形,其外接圆内部不包含任何一个基点(空圆性)
理由是这样,假如包含某个基点,那么外接圆圆心到这个基点的距离比那三个基点更小,应该被划分在这个基点的泰森多边形内,矛盾
了解这个性质,能够帮助我们理解Voronoi图的更高效算法,同时也是Delaunay三角剖分的标准算法:逐点插入法
其思想是维护\(n\)个点的Delaunay三角网,然后加入新点,通过局部调整确保空圆性,生成\(n+1\)个点的Delaunay三角网,复杂度\(O(n^2)\)
参考shine_cherise 笔记:Delaunay三角剖分(Delaunay Triangulation)相关知识(他的复杂度分析中FlipTest的递归深度只有常数级(设为K)不严谨,点如果不随机均匀分布,最坏可能是\(O(n)\)的)
算法概述:
主函数
初始化一个极大三角形
枚举点i:1~n
枚举三角形,找到i所在的三角形abc
加入三角形abi,bci,aci
FlipTest(a,b,i)
FlipTest(b,c,i)
FlipTest(a,c,i)
函数FlipTest(a,b,i)
找到ab边所属另一侧的三角形的第三个顶点d
如果i在abd的外接圆内(不满足空圆性)
删除abi,abd
加入adi,bdi(形象理解,相当于把四边形adbi中间横着的ab边flip了一下)
FlipTest(a,d,i)
FlipTest(b,d,i)
不依赖Delaunay三角网的逐点插入法
另推荐z文聿 计算几何第四周:维诺图(Voronoi Diagram),这篇笔记图文并茂,思路清晰,提及Voronoi图的具体数据结构存储方式、二维Voronoi图的复杂度下界证明和各种算法,包括一个直接在Voronoi图数据结构上进行的逐点插入法(10、Incremental Construction)
不过蒟蒻对其复杂度描述存疑,由于Voronoi图的点数、边数均为\(O(n)\),因此每次插入至多只会付出\(O(n)\)的代价,故复杂度为\(O(n^2)\)
算法概述
初始化极大边界
枚举点i:1~n
枚举点j:1~i-1
找到与点i最近的点near
枚举点j:near开始,再次到near退出
作ij中垂线,与面j交于点p1,p2
更新面i(加入边p2p1)
更新面j(加入边p1p2,删除外侧多余的边)
j:=p2所在边的另一侧面对应的点
极大边界是要额外弄\((\pm INF,\pm INF)\)四个虚拟边界点,初始Voronoi图是沿着坐标轴的四条边
尝试实现了一下,细节非常难处理,尤其是上面提到的多点共圆情况
因为观察发现直线运算,求交点之类的精度损失有点高,有时实际上多点共圆的情况在运算中竟难以判定
至今未找到高效的解决办法,也请大佬们指教
update: 基本解决了,注意的地方见注释
经过计算,在所有平分线落在初始轴边内的前提下,为了使轴边长最小(以提高精度),边界点\(INF\)取\(1+\frac{\sqrt2}{2}\)倍值域,此时轴边长为2INF
不过精度损失还是不小,EPS设1e-10就偶尔和半平面交法拍不上了
//n=2000,time=120ms
//n=10000,time=2000ms
#include<cstdio>
#include<cmath>
#include<iostream>
#include<algorithm>
#define double long double
#define TEST
using namespace std;
const int N=10009,E=30*N;
const double PI=acos(-1),EPS=1e-9,INF=1e4*(1+1/sqrt(2));
struct Point{
double x,y;
Point(){x=y=0;}
Point(double a){x=a;y=0;}
Point(double a,double b){x=a;y=b;}
friend istream&operator>>(istream&is,Point&a){return is>>a.x>>a.y;}
friend ostream&operator<<(ostream&os,Point a){return os<<a.x<<','<<a.y;}
Point operator-(){return Point(-x,-y);}
Point operator+(Point a){return Point(x+a.x,y+a.y);}
Point operator-(Point a){return Point(x-a.x,y-a.y);}
Point operator*(double a){return Point(x*a,y*a);}
Point operator/(double a){return Point(x/a,y/a);}
friend Point operator*(double a,Point b){b.x*=a,b.y*=a;return b;}
Point&operator+=(Point a){x+=a.x,y+=a.y;return*this;}
Point&operator-=(Point a){x-=a.x,y-=a.y;return*this;}
Point&operator*=(double a){x*=a,y*=a;return*this;}
Point&operator/=(double a){x/=a,y/=a;return*this;}
double operator*(Point a){return x*a.x+y*a.y;}
double operator%(Point a){return x*a.y-y*a.x;}
double Len(){return sqrt(x*x+y*y);}
friend double Dis(Point a,Point b){return (a-b).Len();}
Point Turn(double r){double c=cos(r),s=sin(r);return Point(x*c-y*s,y*c+x*s);}
Point Turn90(){return Point(-y,x);}
bool operator==(Point a){return fabs(x-a.x)<EPS&&fabs(y-a.y)<EPS;}
bool operator!=(Point a){return fabs(x-a.x)>EPS||fabs(y-a.y)>EPS;}
};
int ecnt=1,ehead[N],face[E],suc[E];
Point a[N],p[E];
Point Intersect(Point a,Point av,Point b,Point bv){//直线求交点
return a+av*(bv%(b-a))/(bv%av);
}
void AddEdge(Point a,Point b,int af,int bf){//连边
p[++ecnt]=a;face[ecnt]=af;
p[++ecnt]=b;face[ecnt]=bf;
}
int Cut(Point m,Point mv,int e,int f){//有向直线(m,mv)切割边e所在面,另一侧划分给面f,返回翻边
int ein=e,eout,esuc;//切入边,切出边,后继
Point pin,pout;//切入点,切出点
while(true){//寻找切入边
esuc=suc[ein];
if(mv%(p[esuc]-p[ein])<0){
pin=Intersect(p[ein],p[esuc]-p[ein],m,mv);//传参顺序可能影响后面点积判断误差
if(pin==p[esuc]||(pin-p[ein])*(pin-p[esuc])/Dis(pin,p[esuc])<-EPS)
break;//点积判断要避免小数误差放大判断失效,加了个/Dis(pin,p[esuc])
}
ein=esuc;
if(ein==e)//未切入
return -1;
}
eout=suc[ein];
while(true){//寻找切出边
esuc=suc[eout];
if(mv%(p[esuc]-p[eout])>0){
pout=Intersect(p[eout],p[esuc]-p[eout],m,mv);
if(pout==p[esuc]||(pout-p[eout])*(pout-p[esuc])/Dis(pout,p[esuc])<-EPS)
break;//点积判断同上
}
eout=esuc;
if(eout==ein)//切于一个点,不算切入
return -1;
}
AddEdge(pin,pout,face[e],f);
p[eout]=pout;
suc[ein]=ecnt^1;
suc[ecnt^1]=pout==p[esuc]?esuc:eout;//处理退化情况
suc[ecnt]=ecnt-2;
ehead[face[e]]=ein;
return eout;
}
#define DEBUG(a,l,r) for(int i=l;i<=r;++i)cout<<#a<<'['<<i<<"]="<<a[i]<<endl;cout<<endl;
int main(){
freopen("in.in","r",stdin);
freopen("incremental.out","w",stdout);
int n,w,h;
cin>>n>>w>>h;
//初始化INF边界
a[n+1]=Point( INF, INF);
a[n+2]=Point(-INF, INF);
a[n+3]=Point(-INF,-INF);
a[n+4]=Point( INF,-INF);
AddEdge(Point(0,2*INF), Point(0,0),n+1,n+2);
AddEdge(Point(-2*INF,0),Point(0,0),n+2,n+3);
AddEdge(Point(0,-2*INF),Point(0,0),n+3,n+4);
AddEdge(Point(2*INF,0), Point(0,0),n+4,n+1);
ehead[n+1]=2,suc[2]=9,suc[9]=8;
ehead[n+2]=4,suc[4]=3,suc[3]=2;
ehead[n+3]=6,suc[6]=5,suc[5]=4;
ehead[n+4]=8,suc[8]=7,suc[7]=6;
//算法主体
for(int i=1;i<=n;++i){
cin>>a[i];
//寻找点i的最近点
int near;
double neardis=INF;
if(i==1)
near=n+(a[1].y>0?(a[1].x>0?1:2):(a[1].x<0?3:4));
else
for(int j=1;j<i;++j)
if(neardis>Dis(a[i],a[j]))
near=j,neardis=Dis(a[i],a[j]);
//构建点i的多边形
ehead[i]=ecnt+2;
int e=ehead[near];
do{
e=Cut((a[i]+a[face[e]])/2,(a[i]-a[face[e]]).Turn90(),e,i)^1;
}while(face[e]!=near);
suc[ehead[i]]=ecnt;
// DEBUG(ehead,1,n+4);
// DEBUG(face,2,ecnt);
// DEBUG(suc,2,ecnt);
// DEBUG(p,2,ecnt);
}
//加入长方形边界
double ans=0;
for(int i=1;i<=n;++i){
Cut(Point(0,0),Point(1,0),ehead[i],0);
Cut(Point(w,0),Point(0,1),ehead[i],0);
Cut(Point(w,h),Point(-1,0),ehead[i],0);
Cut(Point(0,h),Point(0,-1),ehead[i],0);
int cnt=0,e=ehead[i];
do{
if(ans<Dis(a[i],p[e]))ans=Dis(a[i],p[e]);
++cnt;
e=suc[e];
}while(e!=ehead[i]);
#ifdef TEST//测试生成多边形的边数,检查是否成功处理退化情况
cout<<cnt<<endl;
#endif
}
cout<<ans<<endl;
return 0;
}
点均匀随机分布前提下对逐点插入法的优化
纸异兽 三角剖分算法(delaunay)中提到了将点先按\(x\)或\(y\)坐标排序,再逐个插入的优化(但他的算法实现可能有误)
这样做的原理是:
朴素方法每次插入时,都需要\(O(n)\)次枚举三角形,以确定点在哪些三角形中
排序后,待插入点都在所有三角形的右侧
假如某个三角形的外接圆在插入点的左侧,那么它将永远不会被插入
因此我们只需保存包含将来可能被插入的三角形的链表,以供遍历
在点均匀随机分布前提下,链表里的三角形大概是整个Delaunay三角网的最右边一层,蒟蒻猜测其数量是\(O(\sqrt n)\)的
再加上同样是点均匀随机分布前提下,fliptest的次数大概非常少,能当成常数
那么优化后的复杂度也就降到了\(O(n\sqrt n)\)
不依赖三角网的逐点插入法同理,链表里只保留最右侧x坐标大于等于待插入点x坐标的多边形面
实现如下
//n=10000,time=280ms
#include<cstdio>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<list>
#define double long double
#define TEST
using namespace std;
const int N=10009,E=50*N;
const double PI=acos(-1),EPS=1e-9,INF=1e4*(1+1/sqrt(2));
struct Point{
double x,y;
Point(){x=y=0;}
Point(double a){x=a;y=0;}
Point(double a,double b){x=a;y=b;}
friend istream&operator>>(istream&is,Point&a){return is>>a.x>>a.y;}
friend ostream&operator<<(ostream&os,Point a){return os<<a.x<<','<<a.y;}
Point operator-(){return Point(-x,-y);}
Point operator+(Point a){return Point(x+a.x,y+a.y);}
Point operator-(Point a){return Point(x-a.x,y-a.y);}
Point operator*(double a){return Point(x*a,y*a);}
Point operator/(double a){return Point(x/a,y/a);}
friend Point operator*(double a,Point b){b.x*=a,b.y*=a;return b;}
Point&operator+=(Point a){x+=a.x,y+=a.y;return*this;}
Point&operator-=(Point a){x-=a.x,y-=a.y;return*this;}
Point&operator*=(double a){x*=a,y*=a;return*this;}
Point&operator/=(double a){x/=a,y/=a;return*this;}
double operator*(Point a){return x*a.x+y*a.y;}
double operator%(Point a){return x*a.y-y*a.x;}
double Len(){return sqrt(x*x+y*y);}
friend double Dis(Point a,Point b){return (a-b).Len();}
Point Turn(double r){double c=cos(r),s=sin(r);return Point(x*c-y*s,y*c+x*s);}
Point Turn90(){return Point(-y,x);}
bool operator==(const Point&a){return fabs(x-a.x)<EPS&&fabs(y-a.y)<EPS;}
bool operator!=(const Point&a){return fabs(x-a.x)>EPS||fabs(y-a.y)>EPS;}
};
int ecnt=1,ehead[N],face[E],suc[E],id[N];
Point a[N],p[E];
double maxx[N];
list<int>li;
Point Intersect(Point a,Point av,Point b,Point bv){//直线求交点
return a+av*(bv%(b-a))/(bv%av);
}
void AddEdge(Point a,Point b,int af,int bf){//连边
p[++ecnt]=a;face[ecnt]=af;
p[++ecnt]=b;face[ecnt]=bf;
}
int Cut(Point m,Point mv,int e,int f){//有向直线(m,mv)切割边e所在面,另一侧划分给面f,返回翻边
int ein=e,eout,esuc;//切入边,切出边,后继
Point pin,pout;//切入点,切出点
while(true){//寻找切入边
esuc=suc[ein];
if(mv%(p[esuc]-p[ein])<0){
pin=Intersect(p[ein],p[esuc]-p[ein],m,mv);//传参顺序可能影响后面点积判断误差
if(pin==p[esuc]||(pin-p[ein])*(pin-p[esuc])/Dis(pin,p[esuc])<-EPS)
break;//点积判断要避免小数误差放大判断失效,加了个/Dis(pin,p[esuc])
}
ein=esuc;
if(ein==e)//未切入
return -1;
}
eout=suc[ein];
while(true){//寻找切出边
esuc=suc[eout];
if(mv%(p[esuc]-p[eout])>0){
pout=Intersect(p[eout],p[esuc]-p[eout],m,mv);
if(pout==p[esuc]||(pout-p[eout])*(pout-p[esuc])/Dis(pout,p[esuc])<-EPS)
break;//点积判断同上
}
eout=esuc;
if(eout==ein)//切于一个点,不算切入
return -1;
}
AddEdge(pin,pout,face[e],f);
p[eout]=pout;
suc[ein]=ecnt^1;
suc[ecnt^1]=pout==p[esuc]?esuc:eout;//处理退化情况
suc[ecnt]=ecnt-2;
ehead[face[e]]=ein;
maxx[face[e]]=0;//更新面最右侧x
e=ein;
do{
maxx[face[e]]=max(maxx[face[e]],p[e].x);
e=suc[e];
}while(e!=ein);
maxx[f]=max(maxx[f],pout.x);
return eout;
}
#define DEBUG(a,l,r) for(int i=l;i<=r;++i)cout<<#a<<'['<<i<<"]="<<a[i]<<endl;cout<<endl;
int main(){
freopen("in.in","r",stdin);
freopen("incremental1.out","w",stdout);
int n,w,h;
cin>>n>>w>>h;
//初始化INF边界
a[n+1]=Point( INF, INF);
a[n+2]=Point(-INF, INF);
a[n+3]=Point(-INF,-INF);
a[n+4]=Point( INF,-INF);
AddEdge(Point(0,2*INF), Point(0,0),n+1,n+2);
AddEdge(Point(-2*INF,0),Point(0,0),n+2,n+3);
AddEdge(Point(0,-2*INF),Point(0,0),n+3,n+4);
AddEdge(Point(2*INF,0), Point(0,0),n+4,n+1);
ehead[n+1]=2,suc[2]=9,suc[9]=8;
ehead[n+2]=4,suc[4]=3,suc[3]=2;
ehead[n+3]=6,suc[6]=5,suc[5]=4;
ehead[n+4]=8,suc[8]=7,suc[7]=6;
//算法主体
for(int i=1;i<=n;++i){
cin>>a[i];
id[i]=i;
}
sort(id+1,id+n+1,[](int x,int y){return a[x].x<a[y].x;});
for(int i=1;i<=n;++i){
//寻找点i的最近点
int near;
double neardis=INF;
if(i==1)
near=n+(a[1].y>0?(a[1].x>0?1:2):(a[1].x<0?3:4));
else{
auto iter=li.begin();
while(iter!=li.end()){
if(a[id[i]].x>maxx[*iter])
iter=li.erase(iter);//链表中去掉无用面,减少枚举
else{
if(neardis>Dis(a[id[i]],a[*iter]))
near=*iter,neardis=Dis(a[id[i]],a[*iter]);
++iter;
}
}
}
//构建点i的多边形
ehead[id[i]]=ecnt+2;
int e=ehead[near];
do{
e=Cut((a[id[i]]+a[face[e]])/2,(a[id[i]]-a[face[e]]).Turn90(),e,id[i])^1;
}while(face[e]!=near);
suc[ehead[id[i]]]=ecnt;
li.push_front(id[i]);
}
//加入长方形边界
double ans=0;
for(int i=1;i<=n;++i){
Cut(Point(0,0),Point(1,0),ehead[i],0);
Cut(Point(w,0),Point(0,1),ehead[i],0);
Cut(Point(w,h),Point(-1,0),ehead[i],0);
Cut(Point(0,h),Point(0,-1),ehead[i],0);
int cnt=0,e=ehead[i];
do{
if(ans<Dis(a[i],p[e]))ans=Dis(a[i],p[e]);
++cnt;
e=suc[e];
}while(e!=ehead[i]);
#ifdef TEST//测试生成多边形的边数,检查是否成功处理退化情况
cout<<cnt<<endl;
#endif
}
cout<<ans<<endl;
return 0;
}
update
不依赖三角网的逐点插入法中,每次要\(O(n)\)寻找最近点,这个是不是可以KDtree做呀
不过要动态插点,那么可以事先将点集random_shuffle后依次插入,或者写替罪羊树版的KDtree
点均匀随机分布前提下,每个多边形的边数大概非常少,能当成常数
合起来期望是\(O(n\log n)\)的,不过常数也够大,加上难写(蒟蒻还不会KDtree)
这个不适用于一般情况的方案就没什么实现必要了,权当口胡玩玩
分治法
太难懂了~复杂度\(O(n\log n)\)
蒟蒻尝试不加证明地用直观的方式说明这个算法过程
把点集从中间切成两半,分别求出两边的Voronoi图,然后合并
合并后的Voronoi图应该怎样从合并前的变过去呢?
来看一张图,中间的图由左边和右边合并成
其中只有标红的边是新加入的,从两个点集的中间曲折地穿过,我们称之为轮廓线
这些边都是由哪些点对的垂直平分线组成的呢?从下往上数,\((3,5)(3,6)(2,6)(4,6)(4,7)\)
有没有发现,从前一个点对到后一个点对,总是有一个点是一样的
算法概述
函数merge(有序点集S)
如果|S|<=3
直接构造Voronoi图并返回
merge(S1)
merge(S2)
找到轮廓线的第一条边,p1p2的垂直平分线
遍历轮廓线,直到最后一条边
分别在S1,S2中做射线,与面p1、面p2产生交点
如果S1的交点更近
p1更新为交点所在边另一侧面对应基点
否则
p2更新为交点所在边另一侧面对应基点
在Voronoi图中连边
返回新Voronoi图
这些步骤中,做射线、翻至边的另一侧等操作在逐点插入法里都实现了,唯一麻烦的是找到轮廓线的第一条边和最后一条边
目前看到的说法都是,这两条边是两个点集凸包的两条外公切线的垂直平分线
如果真要这么做的话,还要额外维护点集凸包,加上实现一个单调指针扫描的求公切线的算法,又要再来一遍不胜枚举的边界情况判断ヽ(≧□≦)ノ
苦苦思索之后,终于想到了一个办法
整个轮廓线上,只有第一条边和最后一条边延伸到无穷远处
之前逐点插入法里不是加入了边界点嘛,那在算法中,这两条边会终止于边界点对应的多边形面
所以,把两边Voronoi图的4个边界点多边形都弄出来,找到它们的特殊交点,这一定是第一条边和最后一条边的起止点
拿上面那张图的例子来说
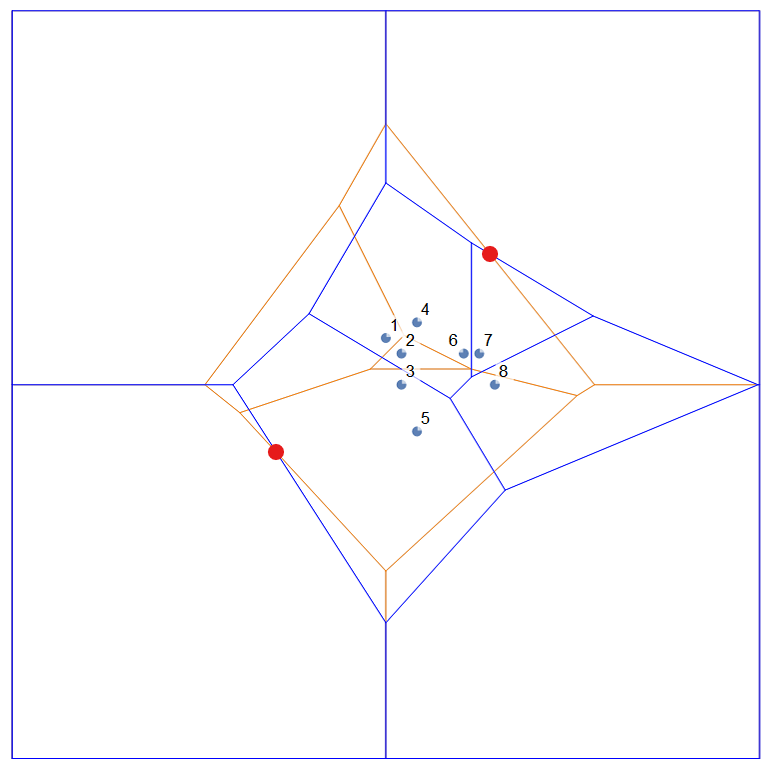
这就好多了,编程时间和运行时间都省了,岂不美哉
参考:
Samuel Peterson COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS
zball Delaunay剖分与平面欧几里得距离最小生成树
扫描线法
太难懂了~复杂度\(O(n\log n)\)
问题变种
相关题目
找到的模板题挺少的,如果大佬们知道可以留言,蒟蒻会及时添加上去
LOJ6409「ICPC World Finals 2018」熊猫保护区
百度之星2008初赛 T4.圆面覆盖(未在OJ上找到该题)
问题背景
在平面上有一个长为L,宽为W的长方形,左下角坐标为(0,0),右上角坐标为(L,W)。给定一些圆,第i个圆的圆心坐标为(xi,yi),半径为Ri。
你的任务是求最小的正实数k,使得把每个圆的半径变为原来的k倍后(即:第i个圆半径变为kRi,圆心位置不变),长方形将被这些圆完全覆盖。换句话说,长方形内部或边界上的任意点均至少在一个圆的内部或边界上。输入格式
输入第一行包含三个整数n, L, W(1<=n<=50,1<=L,W<=1000),即圆的个数、长方形的长和宽。
以下n行,每行三个不超过1000的正整数xi, yi和Ri输出格式
仅一行,包含一个实数k,保留小数点后三位。样例输入
1 2 2
1 1 1样例输出
1.414
更新中!
随便想了个小问题,就扯出来一大堆知识点,对于我这个刚入门的蒟蒻,不得不说是一场惨案了TAT



 浙公网安备 33010602011771号
浙公网安备 33010602011771号