CSP-S 2021 初赛解析之完善程序




解析
本题类似 dijkstra ,每次选择已经确定最小操作的数字来转移到其他数字。
其中Vis数组用来表示当前元素的状态是否确定,当Vis[x]为真时,表示数字x最少用多少个4运算可得的状态已经确定。
从第44行代码可知,F[n]表示n的最少方案数。
第34题
初始化状态,首先排除A,B。C选项F[1]=2-->将会得到F[2]=4,显然不对,故选D
第35题
首先排除C和D,但 r 似乎对本题没有任何影响……,应该时出题人有意干扰。
当 Fn 有值时也不一定是最优的,只有当 Fn 作为可以去转移别人的时候才是最优的。故选 A
第36题
类似dijkstra,寻找一个F值最小且状态还不确定的。满足F值最小通过线性查找的方式,故选D
第37题
两个数转移到新的数,只有当这两个数都是最优的时候,才能保证本次转移不会白转移(指其中一个数再更新本次转移作废)。故选 C。







解析
RMQ算法由很多种,ST算法复杂度预处理nlogn,查询O1,线段树预处理On,查询Ologn,下图的四毛子算法实现起来可以预处理On,查询O1。是不是觉得很优秀?尚未经过实际测试,不好说。题意在放代码之前已经说得很清楚了。121行的代码虽然多了点,但出题人的代码风格还是很友好的。四毛子算法理解起来有一定的难度,总结如下:
1.通过原始RMQ系列(n个元素)建立笛卡尔树。这样RMQ问题就变成LCA问题。
2.将笛卡尔树进行DFS求其欧拉系,欧拉系的长度为 \(t=2n-1\),此系列虽然比原来长了一倍,但相邻元素的depth具有\(\pm1\)的特征。这样又将LCA问题转换成RMQ问题。(普通RMQ-->笛卡尔树-->约束RMQ)
3.将约束RMQ系列分成若干块,每块的长度取\(b=(int)\frac{log_2{t}}{2}\),一共可以分成\(c=t/b\)块。
4.针对完整的整数个大块间的RMQ问题,采用ST表解决。\(F[i][j]=max(F[i][j-1],F[i+(1<<(j-1))][j-1]\)。
5.(重点难点)针对一个块内的RMQ问题,其差分数组共\(2^{b-1}\)种,预处理所有情况的最值位置,查询时通过二进制左移右移操作完成。有点懵?后面会通过画图解析。
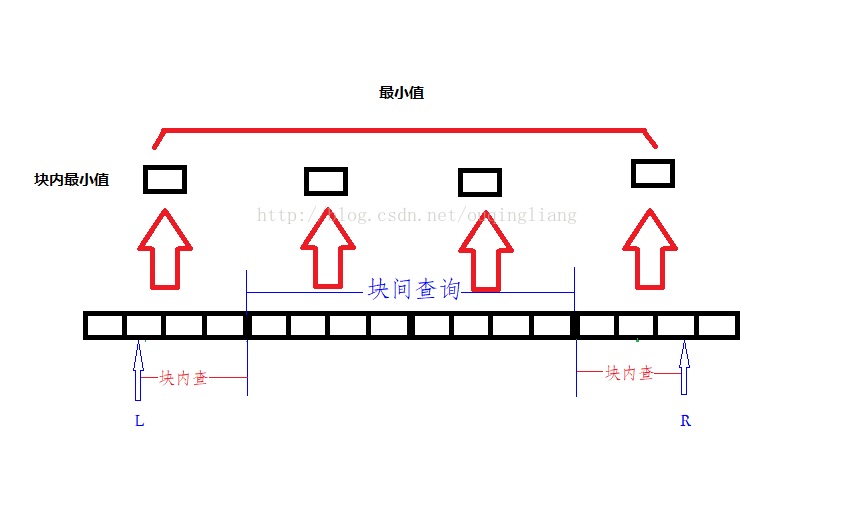
6.如下图所示,一般情况下,对于一个查询,既有块内查询,又有块间查询,则最左,最右边的块搞一次内部查询。然后中间所有块中再做一次块与块之间的查询操作。最后合并到一起取最值即可。
关于建立笛卡尔树
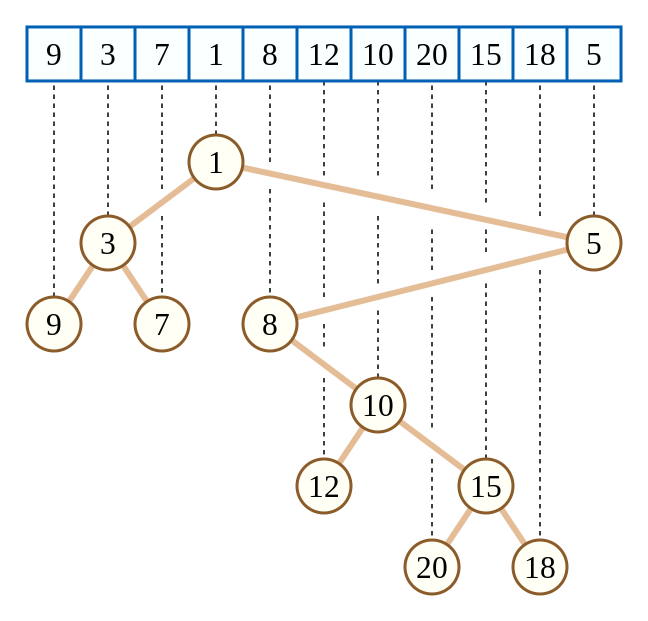
笛卡尔树是一种二叉树,每一个结点由一个键值二元组\((k,w)\)构成。要求\(k\)满足二叉搜索树的性质,而\(w\)满足堆的性质。所谓\(k\),是指下标序号,\(w\)指具体的元素值。如下图,\(20\)对应的\(k\)值为7(序号从0开始),对应的\(w\)值为20。从图中可以看出,\(w\)值满足小根堆性质,\(k\)满足二叉搜索树(左序号<中序号<右序号),且按照图中的中序遍历可以还原出完整的序列。
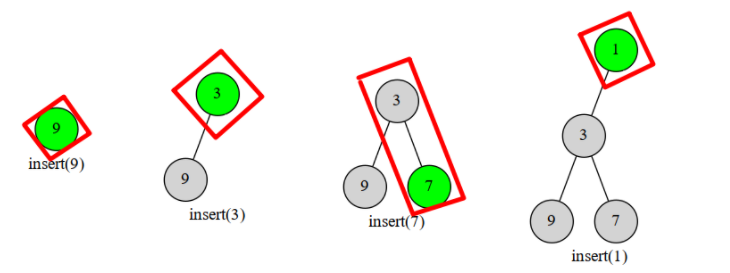
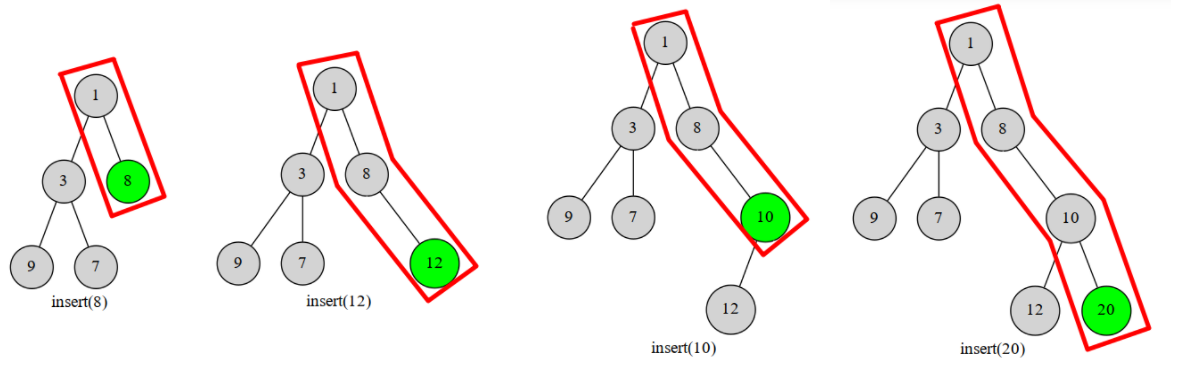
建树方法:维护树的最右链形成单调栈
建树过程:
- 将栈由栈顶到栈底遍历,若栈元素大于当前元素t,则弹出栈,直到在栈中查找到比当前元素p更小的元素s[k]为止。
- 如果找到了,则将s[k]的右儿子设置为t
- 将t的左儿子设置为\(s[k+1]\)(最后一个弹出栈的元素)
- 将t入栈
详细过程如下图描述:
代码:
新建一个大小为 n 的空栈。用 top 来标操作前的栈顶,k 来标记当前栈顶。
For i := 1 to n
k := top
While 栈非空 且 栈顶元素 > 当前元素
k--
if 栈非空
栈顶元素.右儿子 := 当前元素
if k < top
当前元素.左儿子 := 最后一次弹出栈的元素
当前元素入栈
top := k
for (int i = 1; i <= n; i++) {
int k = top;
while (k > 0 && h[stk[k]] > h[i]) k--;
if (k) rs[stk[k]] = i; // rs代表笛卡尔树每个节点的右儿子
if (k < top) ls[i] = stk[k + 1]; // ls代表笛卡尔树每个节点的左儿子
stk[++k] = i;
top = k;
}
第38-40题

第38题选择A,将新元素的左儿子设置为最后一个出栈的元素
第39题选择D,将栈顶元素的右儿子设置为新进来的元素,然后新元素入栈
第40题选A,函数名中有min,故求最小值,按照笛卡尔树的性质,深度越小值越大,根节点元素值最大,符合题意。
关于块内预处理(难点)
根据原始系列\(9 ,3, 7, 1, 8, 12, 10, 20, 15, 18, 5\),将其建立成笛卡尔树后进行dfs的欧拉系列是\(1,3,9,3,7,3,1,5,8,10,12,10,15,20,15,18,15,10,8,5,1\),不妨将这个长度为\(21\)的系列按每\(10\)个元素分块,可以分成\(3\)块,我们拿第\(1\)块为例介绍,第\(1\)块的系列为\(1,3,9,3,7,3,1,5,8,10\),而第\(1\)块的深度系列则为\(0,1,2,1,2,1,0,1,2,3\)(题意将根节点的深度设置为0)。本题要求RMQ的最大值,所以要查找的位置是深度的最小值,不妨设置:若后一个元素的深度小于前一个元素的深度则记为+1,反之记为-1,这样本块的差分关系表如下:
| i*b+0 | i*b+1 | i*b+2 | i*b+3 | i*b+4 | i*b+5 | i*b+6 | i*b+7 | i*b+8 | i*b+9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 9 | 3 | 7 | 3 | 1 | 5 | 8 | 10 |
| 0 | 1 | 2 | 1 | 2 | 1 | 0 | 1 | 2 | 3 |
| 差分 | -1 | -1 | 1 | -1 | 1 | 1 | -1 | -1 | -1 |
第41题


本题选择D,转化为欧拉系列后与Val没有关系,为什么呢?如果还要判断val值,直接原系列就可以,为什么要建立笛卡尔树和欧拉系,不就是为了这个深度\(\pm1\)的约束RMQ吗?
根据第41题的选项,再通过第68行代码,可以算出\(Dif[i]\)表示的是第\(i\)块的差分关系,以刚刚那个10个元素的块为例,其\(Dif=000110100,\)这是一个二进制来表示差分关系的方法。具体如下表显示
| i*b+0 | i*b+1 | i*b+2 | i*b+3 | i*b+4 | i*b+5 | i*b+6 | i*b+7 | i*b+8 | i*b+9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 9 | 3 | 7 | 3 | 1 | 5 | 8 | 10 |
| 0 | 1 | 2 | 1 | 2 | 1 | 0 | 1 | 2 | 3 |
| 差分 | -1 | -1 | 1 | -1 | 1 | 1 | -1 | -1 | -1 |
| 二进制 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
从上表可以得出,Dif=000110100二进制系列中,从最低位开始,依次到最高位(方向从右到左),所对应的j值(块内元素序号,从1开始计算)依次递增(方向从左到右)。所以上表中显示的二进制的方向与该块的dif值的二进制方向恰好相反(001011000与000110100)
第42题

本题选择D。通过69行到76行的代码可以看出,其目的是为了遍历每一个差分二进制(共\(2^{b-1}\)种情况)对应的最值的位置。因为要求深度最小的值,所以才有 if (v<mx) mx=v,v的初始值从0开始计算,碰到深度更小的就执行v-=1,碰到深度更大的就执行v+=1,判断的方向是按系列从左到右,所对应的S值就应该从右到左,故四个选项都是S>>的操作。因为i是从1开始,所以排除A、B。A和B开始就是从S>>1,则块的系列最左边两个元素的差分二进制码就被遗漏了。所以要从S>>0开始计算。如果S右移后对应的二进制位为1,说明深度降低,故选择D。
第43题




