P2453 [SDOI2006]最短距离

题目描述

一种EDIT字母编辑器，它的功能是可以通过不同的变换操作可以把一个源串X [l..m]变换为新的目标串y[1..n]。EDIT提供的变换操作有：

源串中的单个字符可被删除(delete)；

被替换 (replace)；

被复制到目标串中去(copy)；

字符也可被插入(insert)；

源串中的两个相邻字符可进行交换并复制到目标串中去(twiddle)；

在完成其它所有操作之后，源串中余下的全部后缀就可用删至行末的操作删除(kill)。

例如，将源"algorithm"转换成目标串"altruistic"的一种方法是采取下面的操作序列:

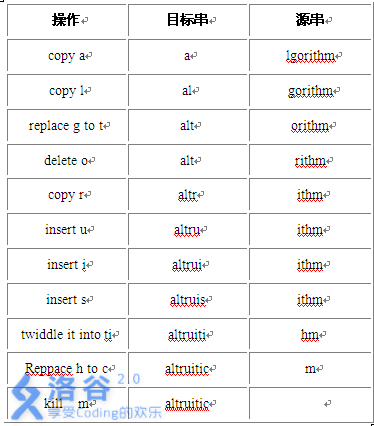
要达到这个结果还可能有其它一些操作序列。

操作delete,replace，copy，insert，twiddle和kill中每一个都有一个相联系的代价cost。例如

cost(delete)=3;
cost(replace)=6;
cost(copy)=5;
cost(insert)=4;
cost(twiddle)=4;
cost(kill)=被删除的串长*cost(delete)-1;

一个给定的操作序列的代价为序列中各操作代价之和。 例如上述操作序列的代价为

3*cost(copy)+2*cost(replace)+cost(delete)+3*cost(insert) + cost(twiddle) +cost(kill)

=3*5+2*6+3+3*4+4+1*3-1=48

编程任务：

给定两个序列x[1..m],y[1..n]和一些操作代价集合，X到Y的最短距离为将X转化为Y的最小的转换序列的代价。请给出一个算法来找出x[1..m]至y[1..n]的最短距离。

输入输出格式

输入格式：

第一行：源序列x[1..m]。（m<200）

第二行：目标序列y[1..n]。(n<200)

第三行：5个正整数（<100）：分别是：delete 、replace 、copy、 insert、 twiddle的代价。

输出格式：

X到Y的最短距离（最小代价和）。

输入输出样例

输入样例#1： 

algorithm
altruistic
3 6 5 4 4

输出样例#1： 

48

 

Solution：

　　本题线性dp。

　　字符串dp套路，定义状态$f[i][j]$表示目标串匹配$i$个原串操作了$j$个的最小代价，并用$w[i]$表示各操作的花费。

　　那么初始状态：$f[0][i\in 1\rightarrow n]=w[1]*i$（删除原串前$i$个字符），$f[i\in 1\rightarrow m][0]=w[4]*$（插入目标串前$i$个字符）。

　　那么转移（取$min$）：

　　　　1、删除：$f[i][j]=f[i][j-1]+w[1]$。

　　　　2、替换：$f[i][j]=f[i-1][j-1]+w[2]$。

　　　　3、复制：前提$s[i]==t[j]$，则$f[i][j]=f[i-1][j-1]+w[3]$。

　　　　4、插入：$f[i][j]=f[i-1][j]+w[4]$。

　　　　5、复制交换：前提$s[i-1]==t[j]$且$s[i]==t[j-1]$，则$f[i][j]=f[i-2][j-2]+w[5]$。

　　最后的时候还得对目标串匹配完了而原串操作到$i$位置进行后缀删除，即$f[m][i]=f[m][i]+(n-i)*w[6]-1$。

代码：

 

/*Code by 520 -- 10.15*/
#include<bits/stdc++.h>
#define il inline
#define ll long long
#define RE register
#define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=205;
int n,m,f[N][N],w[6];
char s[N],t[N];

int main(){
    ios::sync_with_stdio(0);
    memset(f,0x3f,sizeof(f));
    cin>>s+1>>t+1,n=strlen(s+1),m=strlen(t+1);
    For(i,1,5) cin>>w[i];
    f[0][0]=0;
    For(i,1,n) f[0][i]=w[1]*i;
    For(i,1,m) f[i][0]=w[4]*i;
    For(i,1,m) For(j,1,n){
        f[i][j]=min(f[i][j],f[i][j-1]+w[1]);
        f[i][j]=min(f[i][j],f[i-1][j-1]+w[2]);
        if(t[i]==s[j]) f[i][j]=min(f[i][j],f[i-1][j-1]+w[3]);
        f[i][j]=min(f[i][j],f[i-1][j]+w[4]);
        if(i>1&&j>1&&t[i]==s[j-1]&&t[i-1]==s[j]) f[i][j]=min(f[i][j],f[i-2][j-2]+w[5]);
    }
    int ans=0x3f3f3f3f;
    For(i,1,n-1) ans=min(ans,f[m][i]+(n-i)*w[1]-1);
    cout<<min(ans,f[m][n]);
    return 0;
}