CF985F Isomorphic Strings
You are given a string s s s of length n n n consisting of lowercase English letters.
For two given strings s s s and t t t , say S S S is the set of distinct characters of s s s and T T T is the set of distinct characters of t t t . The strings s s s and t t t are isomorphic if their lengths are equal and there is a one-to-one mapping (bijection) f f f between S S S and T T T for which f(si)=ti f(s_{i})=t_{i} f(si)=ti . Formally:
- f(si)=ti f(s_{i})=t_{i} f(si)=ti for any index i i i ,
- for any character
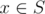 there is exactly one character
there is exactly one character 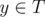 that f(x)=y f(x)=y f(x)=y ,
that f(x)=y f(x)=y f(x)=y , - for any character
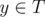 there is exactly one character
there is exactly one character 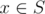 that f(x)=y f(x)=y f(x)=y .
that f(x)=y f(x)=y f(x)=y .
For example, the strings "aababc" and "bbcbcz" are isomorphic. Also the strings "aaaww" and "wwwaa" are isomorphic. The following pairs of strings are not isomorphic: "aab" and "bbb", "test" and "best".
You have to handle m m m queries characterized by three integers x,y,len x,y,len x,y,len ( 1<=x,y<=n−len+1 1<=x,y<=n-len+1 1<=x,y<=n−len+1 ). For each query check if two substrings s[x... x+len−1] s[x...\ x+len-1] s[x... x+len−1] and s[y... y+len−1] s[y...\ y+len-1] s[y... y+len−1] are isomorphic.
输入输出格式
输入格式:The first line contains two space-separated integers n n n and m m m ( 1<=n<=2⋅105 1<=n<=2·10^{5} 1<=n<=2⋅105 , 1<=m<=2⋅105 1<=m<=2·10^{5} 1<=m<=2⋅105 ) — the length of the string s s s and the number of queries.
The second line contains string s s s consisting of n n n lowercase English letters.
The following m m m lines contain a single query on each line: xi x_{i} xi , yi y_{i} yi and leni len_{i} leni ( 1<=xi,yi<=n 1<=x_{i},y_{i}<=n 1<=xi,yi<=n , 1<=leni<=n−max(xi,yi)+1 1<=len_{i}<=n-max(x_{i},y_{i})+1 1<=leni<=n−max(xi,yi)+1 ) — the description of the pair of the substrings to check.
输出格式:For each query in a separate line print "YES" if substrings s[xi... xi+leni−1] s[x_{i}...\ x_{i}+len_{i}-1] s[xi... xi+leni−1] and s[yi... yi+leni−1] s[y_{i}...\ y_{i}+len_{i}-1] s[yi... yi+leni−1] are isomorphic and "NO" otherwise.
输入输出样例
7 4
abacaba
1 1 1
1 4 2
2 1 3
2 4 3
YES
YES
NO
YES
说明
The queries in the example are following:
- substrings "a" and "a" are isomorphic: f(a)=a f(a)=a f(a)=a ;
- substrings "ab" and "ca" are isomorphic: f(a)=c f(a)=c f(a)=c , f(b)=a f(b)=a f(b)=a ;
- substrings "bac" and "aba" are not isomorphic since f(b) f(b) f(b) and f(c) f(c) f(c) must be equal to a a a at same time;
- substrings "bac" and "cab" are isomorphic: f(b)=c f(b)=c f(b)=c , f(a)=a f(a)=a f(a)=a , f(c)=b f(c)=b f(c)=b .
#include<bits/stdc++.h> #define il inline #define ll long long #define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++) #define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--) using namespace std; const int N=200005,M=131,mod2=998244353,mod1=19260817; int n,m,x,y,len; ll f[N][27],sum[N],a[27],b[27]; char s[N]; il int gi(){ int a=0;char x=getchar();bool f=0; while((x<'0'||x>'9')&&x!='-')x=getchar(); if(x=='-')x=getchar(),f=1; while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar(); return f?-a:a; } il bool check(){ For(i,1,26) a[i]=(f[x+len-1][i]-f[x-1][i]*sum[len]%mod1+mod1)%mod1, b[i]=(f[y+len-1][i]-f[y-1][i]*sum[len]%mod1+mod1)%mod1; sort(a+1,a+27),sort(b+1,b+27); For(i,1,26) if(a[i]!=b[i])return 0; return 1; } int main(){ n=gi(),m=gi(); scanf("%s",s+1); sum[0]=1; For(i,1,n) { sum[i]=(sum[i-1]*M)%mod1; For(j,1,26) f[i][j]=(f[i-1][j]*M%mod1+(s[i]=='a'+j-1?1:0))%mod1; } while(m--){ x=gi(),y=gi(),len=gi(); (check())?puts("YES"):puts("NO"); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号