P1712 [NOI2016]区间

题目描述

在数轴上有 NN 个闭区间 [l_1,r_1],[l_2,r_2],...,[l_n,r_n][l1​,r1​],[l2​,r2​],...,[ln​,rn​] 。现在要从中选出 MM 个区间，使得这 MM 个区间共同包含至少一个位置。换句话说，就是使得存在一个 xx ，使得对于每一个被选中的区间 [l_i,r_i][li​,ri​] ，都有 l_i≤x≤r_ili​≤x≤ri​ 。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 [l_i,r_i][li​,ri​] 的长度定义为 r_i-l_iri​−li​ ，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 -1−1 。

输入输出格式

输入格式：

 

第一行包含两个正整数 N,MN,M 用空格隔开，意义如上文所述。保证 1≤M≤N1≤M≤N

接下来 NN 行，每行表示一个区间，包含用空格隔开的两个整数 l_ili​ 和 r_iri​ 为该区间的左右端点。

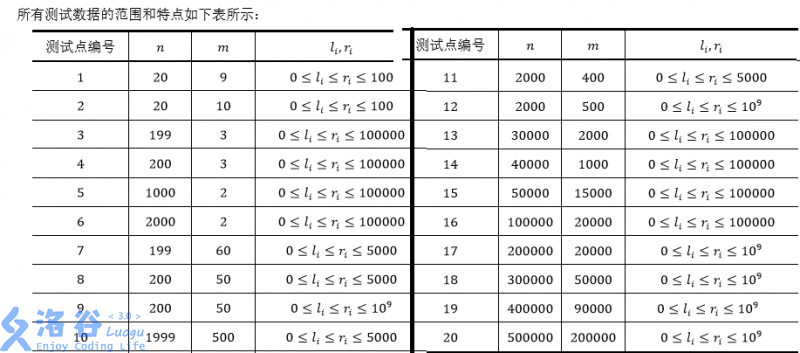
N<=500000,M<=200000,0≤li≤ri≤10^9N<=500000,M<=200000,0≤li≤ri≤109

 

输出格式：

 

只有一行，包含一个正整数，即最小花费。

 

输入输出样例

输入样例#1： 

6 3
3 5
1 2
3 4
2 2
1 5
1 4

输出样例#1： 

2

说明

 

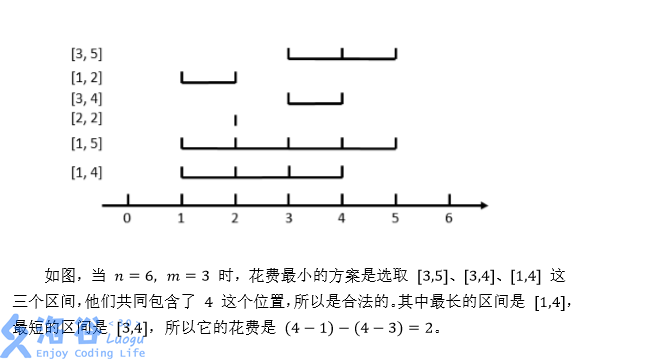
Solution：

　　今天PKU学长HRZ讲课，说到了本题，然后思路比较巧妙。

　　方法就是对区间离散后，按原长度从小到大排序，然后用一个队列维护两个指针$l,r$，$O(n)$的去加入区间$s[l,r]+=1$，用线段树维护区间最大值，若区间最大值$\geq m$则从前往后把加入的区间删除，直到区间最大值刚好$< m$，那么用$l-1$所保存的长度和当前加入的区间长度差去更新答案，然后就没了。

代码：

 

#include<bits/stdc++.h>
#define il inline
#define ll long long 
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
const int N=800005;
int n,m,maxn[N<<3],add[N<<3],ans=0x7fffffff;
int l=1,r;
int *lst[N<<1],cnt,tot;
struct node{
    int l,r,len;
    bool operator<(const node &a)const{return len<a.len;}
}a[N],Q[N];

il bool cmp(const int *a,const int *b) {return *a<*b;}

il int gi(){
    int a=0;char x=getchar();bool f=0;
    while((x<'0'||x>'9')&&x!='-')x=getchar();
    if(x=='-')x=getchar(),f=1;
    while(x>='0'&&x<='9')a=(a<<1)+(a<<3)+x-48,x=getchar();
    return f?-a:a;
}

il void pushup(int rt){maxn[rt]=max(maxn[rt<<1],maxn[rt<<1|1]);}

il void pushdown(int rt,int len){
    if(add[rt]){
        add[rt<<1]+=add[rt],
        add[rt<<1|1]+=add[rt];
        maxn[rt<<1]+=add[rt],
        maxn[rt<<1|1]+=add[rt];
        add[rt]=0;
    }
}

il void update(int L,int R,int k,int l,int r,int rt){
    pushdown(rt,r-l+1);
    if(L<=l&&R>=r){maxn[rt]+=k;add[rt]=k;return;}
    int m=l+r>>1;
    if(L<=m) update(L,R,k,lson);
    if(R>m) update(L,R,k,rson);
    pushup(rt);
}

int main(){
    n=gi(),m=gi();
    For(i,1,n) a[i].l=gi(),a[i].r=gi(),a[i].len=a[i].r-a[i].l,lst[++cnt]=&a[i].l,lst[++cnt]=&a[i].r;
    sort(lst+1,lst+cnt+1,cmp);
    int k=-1;
    For(i,1,cnt) {
        if(*lst[i]!=k) k=*lst[i],*lst[i]=++tot;
        else *lst[i]=tot;
    }
    sort(a+1,a+n+1);
    For(i,1,n) {
        Q[++r].l=a[i].l,Q[r].r=a[i].r,Q[r].len=a[i].len;
        update(a[i].l,a[i].r,1,1,tot,1);
        if(maxn[1]>=m){
            while(l<=r&&maxn[1]>=m){
                update(Q[l].l,Q[l].r,-1,1,tot,1);
                l++;
            }
            if(maxn[1]<m) ans=min(a[i].len-Q[l-1].len,ans);
        }
    }
    cout<<(ans==0x7fffffff?-1:ans);
    return 0;
}