P4467 [SCOI2007]k短路

题目描述

有 n 个城市和 m 条单向道路，城市编号为 1 到 n 。每条道路连接两个不同的城市，且任意两条道路要么起点不同要么终点不同，因此 n 和 m 满足 m \le n(n-1)m≤n(n−1) 。

给定两个城市a和b，可以给a到b的所有简单路（所有城市最多经过一次，包括起点和终点）排序：先按长度从小到大排序，长度相同时按照字典序从小到大排序。你的任务是求出a到b的第 k 短路

输入输出格式

输入格式：

 

输入第一行包含五个正整数n, m, k, a, b。

以下m行每行三个整数u, v, l，表示从城市u到城市v有一条长度为l的单向道路。

 

输出格式：

 

如果a到b的简单路不足k条，输出No，否则输出第k短路：从城市a开始依次输出每个到达的城市，直到城市b，中间用减号"-"分割。

 

输入输出样例

输入样例#1： 

5 20 10 1 5
1 2 1
1 3 2
1 4 1
1 5 3
2 1 1
2 3 1
2 4 2
2 5 2
3 1 1
3 2 2
3 4 1
3 5 1
4 1 1
4 2 1
4 3 1
4 5 2
5 1 1
5 2 1
5 3 1
5 4 1

输出样例#1： 

1-2-4-3-5

输入样例#2： 

4 6 1 1 4
2 4 2
1 3 2
1 2 1
1 4 3
2 3 1
3 4 1

输出样例#2： 

1-2-3-4

输入样例#3： 

3 3 5 1 3
1 2 1
2 3 1
1 3 1

输出样例#3： 

No

说明

第一个例子有5个城市，所有可能出现的道路均存在。从城市1到城市5一共有5条简单路，排序如下：

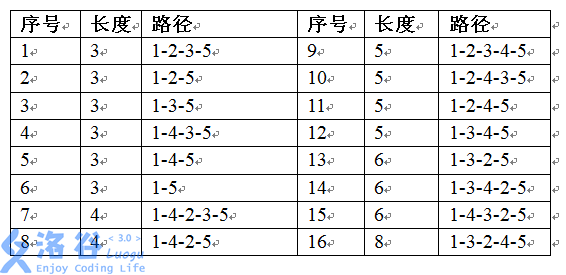
20%的数据满足：n<=5

40%的数据满足：n<=30

100%的数据满足：2<=n<=50, 1<=k<=200

 

Solution：

　　本题真的难写，比上一道k短路板子题难多了（然而本题为紫，板子为黑，神奇！）。

　　题意就是以长度为第一关键字，字典序为第二关键字，求第k小路径。

　　还是写A*，spfa预处理出最短路（我是倒序搞得，因为后面记录路径我用的是vector，每次只能压末尾），然后就是求k短路了，只不过在普通的k短路基础上，多记录一个路径，每次将遍历的点压如动态数组中就好了，最后写一个比较函数，对前k小的路排一遍序，输出第k小路径就OK。

　　（太难调了，卡STL堆的空间，建议手写堆，反正我是特判过的·~·）

代码：

 

#include<bits/stdc++.h>
#define il inline
#define ll long long
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)>(b)?(b):(a))
using namespace std;
const int N=5005,inf=233333333;
int n,m,k,s,t,tot,dis[N];
int to[N],net[N],w[N],h[N],cnt1,To[N],Net[N],W[N],H[N],cnt2;
bool vis[N];
struct node {
    int f,g,id;
    bool vis[55];
    vector<int>path;
    bool operator<(const node a)const {return f==a.f?g>a.g:f>a.f;}
}tmp,tp;

priority_queue<node>Q;

il bool cmp(const node &a,const node &b){
    if(a.f!=b.f)return a.f<b.f;
    int la=a.path.size(),lb=b.path.size(),L;
    L=la>lb?lb:la;
    For(i,0,L-1) if(a.path[i]!=b.path[i]) return a.path[i]<b.path[i];
    return la<lb;
}

il int gi(){
    int a=0;char x=getchar();
    while(x<'0'||x>'9')x=getchar();
    while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar();
    return a;
}

il void add(int u,int v,int c){
    to[++cnt1]=v,net[cnt1]=h[u],h[u]=cnt1,w[cnt1]=c;
    To[++cnt2]=u,Net[cnt2]=H[v],H[v]=cnt2,W[cnt2]=c;
}

il void spfa(){
    queue<int>q;
    For(i,1,n) dis[i]=inf;
    dis[t]=0;vis[t]=1;q.push(t);
    while(!q.empty()){
        int u=q.front();q.pop();vis[u]=0;
        for(int i=H[u];i;i=Net[i])
            if(dis[To[i]]>dis[u]+W[i]){
                dis[To[i]]=dis[u]+W[i];
                if(!vis[To[i]])q.push(To[i]),vis[To[i]]=1;
            }
    }
}

vector<node>mp;

il void Astar(){
    if(dis[s]==inf)return;
    tmp.path.push_back(s),tmp.g=0,tmp.f=dis[s],tmp.id=s,tmp.vis[s]=1;
    Q.push(tmp);
    while(!Q.empty()){
        if(Q.size()>300000)break;
        tmp=Q.top();Q.pop();
        if(tmp.id==t){
            tot++;
            mp.push_back(tmp);
            if(tot>=k&&mp[k-1].f<tmp.f)break;
        }
        for(int i=h[tmp.id];i;i=net[i]){
            if(tmp.vis[to[i]])continue;
            tp=tmp;
            tp.id=to[i];
            tp.g=tmp.g+w[i];
            tp.f=tp.g+dis[to[i]];
            tp.path.push_back(to[i]),tp.vis[to[i]]=1;
            Q.push(tp);
        }
    }
    if(mp.size()<k){puts("No");return;}
    sort(mp.begin(),mp.end(),cmp);
    printf("%d",mp[k-1].path[0]);
    For(i,1,mp[k-1].path.size()-1) printf("-%d",mp[k-1].path[i]);
    return;
}

int main(){
    n=gi(),m=gi(),k=gi(),s=gi(),t=gi();
    int u,v,c;
    if (m==759){puts("1-3-10-26-2-30");return 0;}
    For(i,1,m) u=gi(),v=gi(),c=gi(),add(u,v,c);
    spfa();
    Astar();
    return 0;
}