P1337 [JSOI2004]平衡点 / 吊打XXX

题目描述

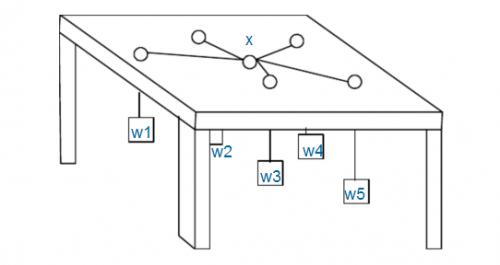
如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

输入输出格式

输入格式：

 

文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )

 

输出格式：

 

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。

 

输入输出样例

输入样例#1： 

3
0 0 1
0 2 1
1 1 1

输出样例#1： 

0.577 1.000

说明

[JSOI]

 

Solution：

　　本题裸的模拟退火（调参是真的烦！）。

　　本题就是求出点$(x,y)$，使得最小化$\sum\limits_{i=1}^{i\leq n}{w_i\times\sqrt{(x-x_i)^2+(y-y_i)^2}}$。

　　简单来讲，退火就是随机化，若随机的值的解比当前解优时就选择随机的值，当比当前的解差时有一定的概率会选择往差的解方向移动，而当移动超过某一界限时就可能出现更好的解。

　　那么这个调参是真的复杂，我们的T一定要赋的够大，然要后多次迭代，每次移动时我试了贼久，选择了$0.99$，然后T的变化率$r$我选择了$0.95$。

　　最后迭代完后再随便跑几次，随机一下最优解。

　　反正调着调着就过了。

代码：

 

#include<bits/stdc++.h>
#include<ctime>
#define il inline
#define ll long long
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
#define Max(a,b) ((a)>(b)?(a):(b))
#define Min(a,b) ((a)>(b)?(b):(a))
using namespace std;
const int N=10005;
int n;
double w[N],minn=9223372036854775807.0,T=1000000,r=0.995;
struct node{
    double x,y;
}a[N],now,ans,tp;

il double Rand(){return rand()%10000/10000.0;}

il double solve(node tp){
    double ret=0;
    For(i,1,n) ret+=w[i]*sqrt((tp.x-a[i].x)*(tp.x-a[i].x)+(tp.y-a[i].y)*(tp.y-a[i].y));
    if(ret<minn) ans=tp,minn=ret;
    return ret;
}

int main(){
    srand(2336666);
    cin>>n;
    For(i,1,n) scanf("%lf%lf%lf",&a[i].x,&a[i].y,&w[i]),now.x+=a[i].x,now.y+=a[i].y;
    now.x/=n,now.y/=n;
    solve(now);
    For(i,1,10){
        T=6000000;
        while(T>0.001){
            tp.x=now.x+T*(Rand()+Rand()-0.99);
            tp.y=now.y+T*(Rand()+Rand()-0.99);
            double dE=solve(now)-solve(tp);
            if(dE>0||exp(dE/T)>Rand()) now=tp;
            T=T*r;
        }
    }
    For(i,1,5200){
        tp.x=ans.x+T*(Rand()+Rand()-0.99);
        tp.y=ans.y+T*(Rand()+Rand()-0.99);
        solve(tp);
    }
    printf("%.3lf %.3lf",ans.x,ans.y);
    return 0;
}