P3275 [SCOI2011]糖果
题目描述
幼儿园里有N个小朋友，lxhgww老师现在想要给这些小朋友们分配糖果，要求每个小朋友都要分到糖果。但是小朋友们也有嫉妒心，总是会提出一些要求，比如小明不希望小红分到的糖果比他的多，于是在分配糖果的时候，lxhgww需要满足小朋友们的K个要求。幼儿园的糖果总是有限的，lxhgww想知道他至少需要准备多少个糖果，才能使得每个小朋友都能够分到糖果，并且满足小朋友们所有的要求。
输入输出格式
输入格式：
输入的第一行是两个整数N，K。接下来K行，表示这些点需要满足的关系，每行3个数字，X，A，B。如果X=1， 表示第A个小朋友分到的糖果必须和第B个小朋友分到的糖果一样多；如果X=2， 表示第A个小朋友分到的糖果必须少于第B个小朋友分到的糖果；如果X=3， 表示第A个小朋友分到的糖果必须不少于第B个小朋友分到的糖果；如果X=4， 表示第A个小朋友分到的糖果必须多于第B个小朋友分到的糖果；如果X=5， 表示第A个小朋友分到的糖果必须不多于第B个小朋友分到的糖果；
输出格式：
输出一行，表示lxhgww老师至少需要准备的糖果数，如果不能满足小朋友们的所有要求，就输出-1。
输入输出样例
说明
【数据范围】
对于30%的数据，保证 N<=100
对于100%的数据，保证 N<=100000
对于所有的数据，保证 K<=100000，1<=X<=5，1<=A, B<=N
Solution：
本题也是$zyys$。。。
巨说是一道缩点+拓扑排序的随便过的题。
然而菜鸡我只能打打思路简单点的差分约束了，重点是如何根据大小关系去建图。
我们不妨假设边$u\rightarrow v$表示的是$v$比$u$大多少，贪心的想到要使得最后的糖果数最小，就尽可能的使得相连的两点糖果数差值尽可能的小（一定是以两者间小的为标准，相等时差为$0$，否则大的数比小的至少大$1$），最后的糖果总数显然最大。
于是我们针对这$5$种情况分别建边（以下出现的$siz[x]$表示的是$x$的糖果数）：
1、当条件为$siz[u]==siz[v]$，则建边$w[u,v]=0,\;w[v,u]=0$（表示$siz[u]==siz[v]$）
2、当条件为$siz[u]<siz[v]$，若$u==v$则直接输出$-1$（显然不成立），否则建边$w[u,v]=1$（表示$siz[v]$比$siz[u]$大$1$）
3、当条件为$siz[u]>=siz[v]$，则建边$w[v,u]=0$（表示$siz[u]==siz[v]$，注意方向$v\rightarrow u$，因为要保证最优性，就必须从小的向大的转移，尽可能的让大的和小的相等）
4、当条件为$siz[u]>siz[v]$，若$u==v$则直接输出$-1$（显然不成立），否则建边$w[v,u]=1$（表示$siz[u]$比$siz[v]$大$1$）
5、当条件为$siz[u]<=siz[v]$，则建边$w[u,v]=0$（表示$siz[v]==siz[u]$，注意方向$u\rightarrow v$，因为要保证最优性，就必须从小的向大的转移，尽可能的让大的和小的相等）
接着，新建一个$0$节点作为源点，向$i=1\rightarrow n$所有点都连边$w[0,i]=1$（表示每个点至少有$1$个糖果）
然后，我们跑一遍最长路（注意！其实求最长路时用$dfs$模拟$spfa$过程，和直接跑$spfa$都能过（我都试写了一遍能$A$），但有坑，后面会讲！），为什么是最长路呢？看看下面这张图（盗的）：
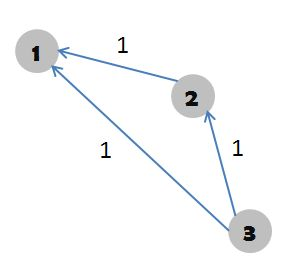
图中的最短路表示$1$点比$3$点大$1$，而另一边的约束条件会使得最后应该是最长路$1$点比$3$点大$2$（很显然，因为肯定得满足约束最多的条件的情况才是合法的！）。
那么求出最长路后(记得判断有环时输出$-1$)，因为要求的是糖果总和，于是累加一下$ans+=dis[i],\;i\in[1,n]$，输出$ans$就好了。
(不看你会后悔：1、$ans$要开$long\;long$。2、醉醉重要的是一个很玄学的东西：后面$0$向$1\rightarrow n$建边时一定要倒序，我也不知道为什么，顺序就是超时，倒序就能起飞。)
代码：
#include<bits/stdc++.h> #define il inline #define ll long long #define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++) #define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--) using namespace std; const int N=300005; int n,k,h[N],net[N],to[N],cnt,w[N],dis[N],tot[N]; bool vis[N]; queue<int>q; il int gi(){ int a=0;char x=getchar(); while(x<'0'||x>'9')x=getchar(); while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar(); return a; } il void add(int u,int v,int c){to[++cnt]=v,net[cnt]=h[u],h[u]=cnt,w[cnt]=c;} int main(){ n=gi(),k=gi(); int u,v,f; while(k--){ f=gi(),u=gi(),v=gi(); if(f==1)add(u,v,0),add(v,u,0); else if(f==2){ if(u==v){cout<<-1;return 0;} add(u,v,1); } else if(f==3)add(v,u,0); else if(f==4){ if(v==u){cout<<-1;return 0;} add(v,u,1); } else if(f==5)add(u,v,0); } Bor(i,1,n)add(0,i,1); vis[0]=1,q.push(0); while(!q.empty()){ int u=q.front();q.pop();vis[u]=0; if(tot[u]==n-1){cout<<-1;return 0;} tot[u]++; for(int i=h[u];i;i=net[i]) if(dis[to[i]]<dis[u]+w[i]){ dis[to[i]]=dis[u]+w[i]; if(!vis[to[i]])vis[to[i]]=1,q.push(to[i]); } } ll ans=0; For(i,1,n)ans+=dis[i]; cout<<ans; return 0; }
