P1801 黑匣子_NOI导刊2010提高（06）

题目描述

Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。

命令只有两种：

ADD(x):把x元素放进BlackBox;

GET:i加1，然后输出Blackhox中第i小的数。

记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：

我们来演示一下一个有11个命令的命令串。（如下图所示）

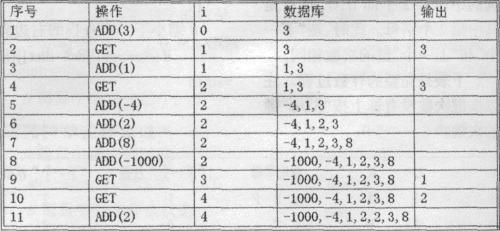
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：

1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。

2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。

输入输出格式

输入格式：

第一行，两个整数，M，N。

第二行，M个整数，表示A(l)

……A(M)。

第三行，N个整数，表示u(l)

…u(N)。

输出格式：

输出Black Box根据命令串所得出的输出串，一个数字一行。

输入输出样例

输入样例#1： 

7 4
3 1 -4 2 8 -1000 2
1 2 6 6

输出样例#1： 

3
3
1
2

说明

对于30%的数据，M≤10000;

对于50%的数据，M≤100000：

对于100%的数据，M≤200000。

 

Solution：

　　本题是一道对顶堆的题目，但还是安利一波权值线段树。。。

　　权值线段树其实很简单，故名思义它的每个叶子节点都有权值(即每个叶子节点维护的是某个确定的数)，它可以很轻松的求出整个区间中的第$k$小的数（注意是整个区间，不是一段区间，权值线段树其实就是弱化的主席树，或者说主席树就是多棵权值线段树）。

　　拿本题做例题。

　　首先，我们对原数组离散化(因为数太大，空间开不下)，这样离散后最多有$200000$个数，就能建树用叶子节点维护每个数了。

　　再讲讲插入操作，其实就是单点修改，对于离散后的数每次找到它所在的叶子节点，使其权值$+1$（说明这个数出现了一次），并维护一段区间的数出现的个数（即区间求和）。

　　然后询问第$k$小的数时，从整个区间$[1,n]$开始递归，当左儿子区间$[l,mid]$中出现的数个数大于等于$k$时，查询左儿子，否则查询右儿子中的第$k-sum[l,mid]$小的数(即左儿子中已有$sum[l,mid]<k$个数，那么整个区间第$k$小的数在右儿子里，且是右儿子中的第$k-sum[l,mid]$小的数)，当查询到$l==r$时返回$l$就$ok$了。

代码：

 

#include<bits/stdc++.h>
#define il inline
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
const int N=2e5+7;
int tr[N<<2],n,m,u[N],s[N],cnt=1;
struct numm{
    ll v;int id;
    bool operator < (numm a){return v<a.v;}
}a[N];
il ll gi(){
    ll a=0;char x=getchar();bool f=0;
    while((x>'9'||x<'0')&&x!='-')x=getchar();
    if(x=='-')x=getchar(),f=1;
    while(x>='0'&&x<='9')a=a*10+x-48,x=getchar();
    return f?-a:a;
}
il void pushup(int rt){tr[rt]=tr[rt<<1]+tr[rt<<1|1];}
il void update(int u,int l,int r,int rt){
    if(l==u&&r==u){tr[rt]++;return;}
    tr[rt]++;
    int m=l+r>>1;
    if(u<=m)update(u,lson);
    else update(u,rson);
    pushup(rt);
}
il int query(int k,int l,int r,int rt){
    if(l==r)return l;
    int m=l+r>>1;
    if(tr[rt<<1]>=k)return query(k,lson);
    else return query(k-tr[rt<<1],rson);
}
int main()
{
    n=gi(),m=gi();
    for(int i=1;i<=n;i++)a[i].v=gi(),a[i].id=i;
    for(int i=1;i<=m;i++)u[i]=gi();
    sort(a+1,a+n+1);
    for(int i=1;i<=n;i++)s[a[i].id]=i;
    for(int i=1;i<=n;i++){
        update(s[i],1,n,1);
        while(i==u[cnt]){
            printf("%lld\n",a[query(cnt,1,n,1)].v);
            ++cnt;
        }
    }
    return 0;
}