在洛谷3369 Treap模板题 中发现的Splay详解
本题的Splay写法(无指针Splay超详细)
前言
首先来讲。。。终于调出来了55555。。。调了整整3天。。。。。
看到大部分大佬都是用指针来实现的Splay。小的只是按照Splay的核心思想和原理来进行的。可能会有不妥之处,还请大佬们指出,谢谢!
那么这个题解存在的意义就是让不会敲Splay的人额。。。会敲Splay啦。。。
基本思想
数据结构
对于Splay,我定义了一个class类(当成struct就行啦。。。个人习惯不同啦),定义名称为“Splay”。
之后在类中,我定义了Splay的主体,即数组e。
e的类型是node类型,包含节点值(v)、父级节点(father)、左孩子(ch[0])、右孩子(ch[1])、包含自己在内的下面共有多少元素(sum)(注意是元素啊!!!不是节点!!!)、该节点所表示的元素出现的次数(recy)。
之后,还在类中定义了n代表当前已经使用的数组编号。points代表整个树总共有多少元素(注意是元素啊!!!不是节点!!!)。
另外,整棵树中,有一个超级根e[0],其右孩子即为树的根。
宏定义了e[0].ch[1]为root,方便访问、理解。并在类的末尾取消定义root,确保外部再定义root变量时不会出现问题,维持其模块性质。
class Splay//存储规则:小左大右,重复节点记录
{
#define root e[0].ch[1] //该树的根节点
private:
class node
{
public:
int v,father;//节点值,父级节点
int ch[2];//左孩子=0,右孩子=1
int sum;//自己+自己下级有多少节点。在根节点为1。
int recy;//记录自己被重复了几次
};
node e[MAXL];//Splay树主体
int n,points;//使用存储数,元素数
……
#undef root
};功能全解
更新当前节点sum值(update)
就是在进行了连接、插入、删除等操作以后使用的一个维护性质的函数。用来确定被update的节点的sum值。
void update(int x)
{
e[x].sum=e[e[x].ch[0]].sum+e[e[x].ch[1]].sum+e[x].recy;
}获取父子关系(identify)
用来确定当前节点到底是父亲的左孩子(0)还是右孩子(1)。
int identify(int x)
{
return e[e[x].father].ch[0]==x?0:1;
}建立父子关系(connect)
用来连接两个点,其中一个点为另一个点的孩子。
注意,这个操作并不能将其他的父子关系一并断开。因为他们与被操作的两个点没有直接的数据联系。例如下图:
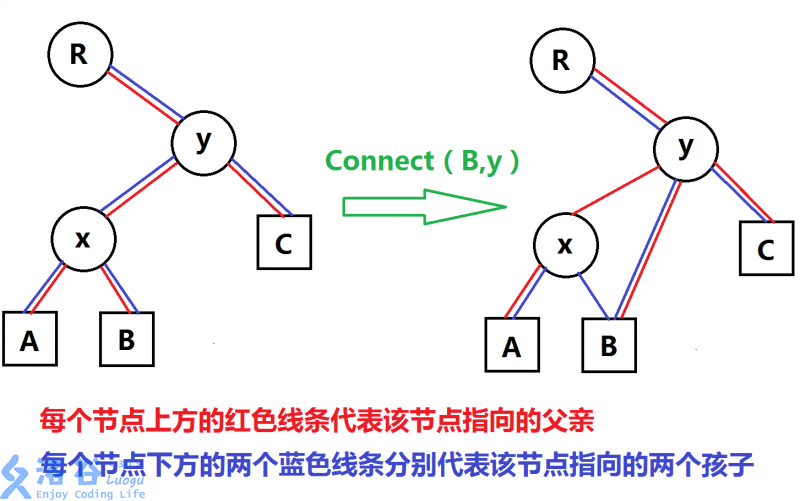
图表明尽管B的父亲已经不是x,但是x的右孩子依旧是B,没有被更新。因此使用过程中应当有更巧妙的设计来避免这样导致的错误发生。
void connect(int x,int f,int son)//连接函数。用法:connect(son,father,左儿子(0)或右儿子(1))
{
e[x].father=f;
e[f].ch[son]=x;
}//作用:将x连接在f的下方。连接方向由son的值决定。旋转节点(rotate)
着重注意的一个函数。这个函数同时实现了左旋和右旋。
所谓的旋转,其实就是指将被指定的节点向上移动一级,并将原有的父级节点作为自己的儿子。如下图:
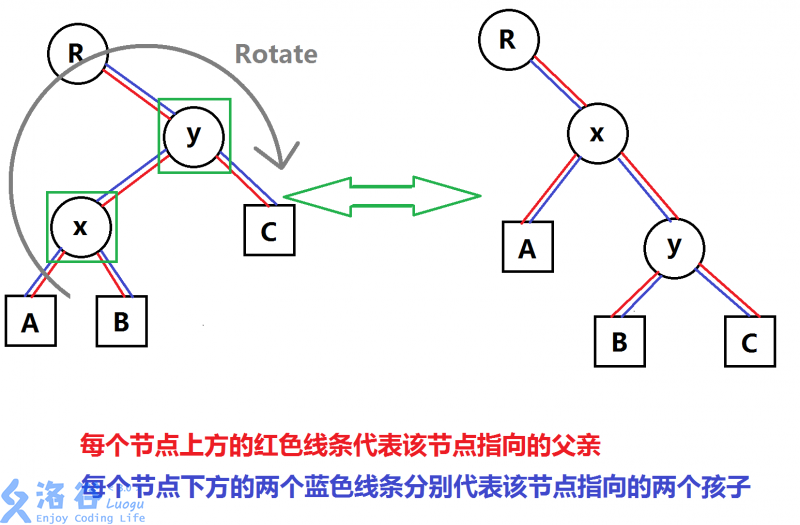
我们可以通过下图原理论证来确定只需要三次connect即可完成旋转。
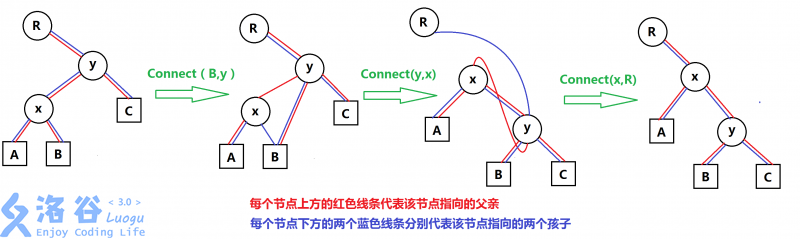
上图代表了右旋。
在图中,A、B、C代表三个子树(可以是空的),x和y代表被旋转的节点。R为y的上级节点,与旋转没有直接关系,但是它的右孩子要进行相应的改变。
在进行完connect函数后,再进行update函数即可完成旋转。
但是旋转总共有两种类型的操作(即左旋和右旋)。在这里,我们需要配合位运算直接达到自动判断和旋转方向决断的目的。
我们知道,对于任意一个自然数,与1进行逻辑异或运算,会得到这样的结果:
0^1=1 1^1=0 2^1=3 3^1=2 4^1=5 5^1=4 ……
也就是说,0对应1,2对应3,4对应5,向后依次推。
既然这样,那么我们的左右儿子节点所代表的编号分别是0和1。也就是说对其中一个取逻辑异或,会得到另一个儿子的标号(即对0取逻辑异或得1,对1取逻辑异或得0)。
通过左旋右旋的性质可以知道,实际改变了父子关系的节点是上图的:x、y、B节点。因为实际上,A、C节点的父子关系并没有发生任何改变。
并且我们能够注意到,x与y节点的连接方向一定是与x和B的连接方向不同的。
那么,我们只需要先通过“identify”函数确定x与y的父子关系,确定到底要向那一边旋转(如果x是y的左孩子,那么就向右旋转。如果x是y的右孩子,那么就向左旋转),然后通过逻辑异或来确定子树“B”究竟应当被连接在y的哪一侧。
void rotate(int x)
{
int y=e[x].father;
int mroot=e[y].father;
int mrootson=identify(y);
int yson=identify(x);
int B=e[x].ch[yson^1];
connect(B,y,yson);connect(y,x,(yson^1));connect(x,mroot,mrootson);
update(y);update(x);
}伸展操作(Splay)
其实就是考虑上旋节点的方式。
在这里,一开始我使用了一种较为偷懒的旋转方式,即能向上旋转就向上旋转。并不考虑上面的状况到底怎样。
其实,标准的写法中,需要考虑两种情况。如下图:
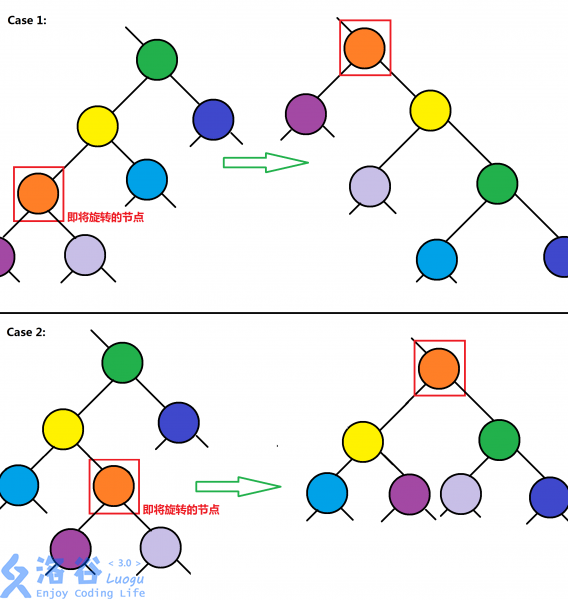
为了防止造成误导,我将不再介绍直接上旋的操作。但事实上,无论是直接上旋还是先判断再上旋,都会有可能进化或者退化原本的树形结构。
我也曾举出过两种操作模式各自进化或者退化树的例子。但是根据交题情况,在洛谷的模板题中,直接上旋的速度更快。然而在湖南的一道省选题中,使用直接上旋的模式却直接导致超时(大概慢了10倍)。所以说在面对大数据的不确定因素下,还是应当选择考虑更多种情况,而不能图方便。
在这里,我的函数实现的操作是:将at节点旋转到to节点所在的位置。
void splay(int at,int to)
{
to=e[to].father;
while(e[at].father!=to)
{
int up=e[at].father;
if(e[up].father==to) rotate(at);
else if(identify(up)==identify(at))
{//对应图中case1
rotate(up);
rotate(at);
}
else
{//对应图中case2
rotate(at);
rotate(at);
}
}
}添加节点(crepoint)和摧毁节点(destroy)
这两个操作是在插入新元素和删除元素过程中使用的函数。
crepoint的作用是获得一个新的树存储位置,然后为这个存储空间写入基本的信息,并返回使用的存储位置编号。
destroy的作用则是使得一个节点完全失效,完全抹除节点信息,防止其他意外的发生。并且添加了一个小小的优化:如果被抹除的节点恰好是存储数组的当前最后一个元素,那么就对存储空间的使用数减1。
实际上,也可以通过一个队列来确定那些节点在中间被挖空了。但这样的操作不仅要牺牲一个O(log N)的时间复杂度,而且事实上并没有太大的用处,因为你开的数组大小一定能够满足极端情况(比如说所有操作都是插入)。
int crepoint(int v,int father)
{
n++;
e[n].v=v;
e[n].father=father;
e[n].sum=e[n].recy=1;
return n;
}
void destroy(int x)
{
e[x].v=e[x].ch[0]=e[x].ch[1]=e[x].sum=e[x].father=e[x].recy=0;
if(x==n) n--;
}查找元素(find)
要实现的功能是找特定值是否在树中以及对应的节点编号。
很简单的实现方式。从根开始向下移动,如果要找的元素比当前节点小,那么就转到自己的左孩子。否则,就转向自己的右孩子,直到节点值等于要找的值。
如果在找到目标值之前,需要走的路已经无法再走(比如说现在到了5,要找的是3,应该往左走,但是5已经没有左孩子了),那么则查找失败,返回失败值(0)。如果查找成功,则返回节点对应的编号。
查找结束后,将被查找的节点旋转到根,以保证树的结构随机性。
int find(int v)
{
int now=root;
while(true)
{
if(e[now].v==v)
{
splay(now,root);
return now;
}
int next=v<e[now].v?0:1;
if(!e[now].ch[next]) return 0;
now=e[now].ch[next];
}
}建树(build)
建树的功能我并没有看懂大佬们的操作到底是什么意思。。。(我觉得应该是将Splay用作线段树的时候使用的功能)所以我写了一个没有上旋操作的insert函数。
首先,从根开始,向下寻找。如果要插入的元素已经在树中,那么将这个节点的recy加1即可。如果没有出现过,那么找一个合适的空的位置。找到位置后,调用crepoint函数,在数组中申请一个新的下标存储元素。
同时注意,在向下寻找的过程中,对被经过的点的sum值加1,因为如果经过这个点,代表要加的点肯定在自己下面,所以自己下面的元素个数加1。
int build(int v)//内部调用的插入函数,没有splay
{
points++;
if(n==0)//特判无点状态
{
root=1;
crepoint(v,0);
}
else
{
int now=root;
while(true)//向下找到一个空节点
{
e[now].sum++;//自己的下级肯定增加了一个节点
if(v==e[now].v)
{
e[now].recy++;
return now;
}
int next=v<e[now].v?0:1;
if(!e[now].ch[next])
{
crepoint(v,now);
e[now].ch[next]=n;
return n;
}
now=e[now].ch[next];
}
}
return 0;
}插入节点(push)
就是在进行完build操作以后,执行一次上旋操作,确保树的结构随机性。
void push(int v)
{
int add=build(v);
splay(add,root);
}删除节点(pop)
将输入值对应的节点在树中移除。
进行这样的操作时,我一开始考虑的是通过逐层的rotate操作将要被删除的节点转到最下方,然后再删除,最后逐层向上改变路径上的sum值。但是考虑到这样的操作可能会一方面导致树的大幅度退化,另一方面相当于要进行两次O(log N)的时间复杂度操作,常数略大,可能会成为一颗定时炸弹。所以为了稳定,还是用了常规的方法:
首先将要删除的节点旋转到根节点的位置。
然后,判断情况:如果要被删除的节点(注意现在它在根的位置)没有左孩子,那么直接摧毁这个节点,并将它的右孩子变成根。
如果自己有左孩子,那么就先把左子树中值最大的元素旋转到根的左孩子位置,然后将根节点的右孩子变成根节点的左孩子的右孩子,然后摧毁节点,并将左孩子变成根。
原理还请读者自己考虑吧,根据二叉排序树的性质。。。
void pop(int v)//删除节点
{
int deal=find(v);
if(!deal) return;
points--;
if(e[deal].recy>1)
{
e[deal].recy--;
e[deal].sum--;
return;
}
if(!e[deal].ch[0])
{
root=e[deal].ch[1];
e[root].father=0;
}
else
{
int lef=e[deal].ch[0];
while(e[lef].ch[1]) lef=e[lef].ch[1];
splay(lef,e[deal].ch[0]);
int rig=e[deal].ch[1];
connect(rig,lef,1);connect(lef,0,1);
update(lef);
}
destroy(deal);
}获取元素的排名(rank)&获取该排名对应的元素值(atrank)
两个函数是互逆的函数。
rank的实现根find差不多,只是在向下走的时候,对于当前已经记录的rank值进行更新(每次调用rank时都初始化为0)。规则是:向左走时,rank值不发生任何改变。向右走之前,要先给rank加上当前节点的左孩子的sum值和recy值。找到对应元素时,再对rank+1。如下图:
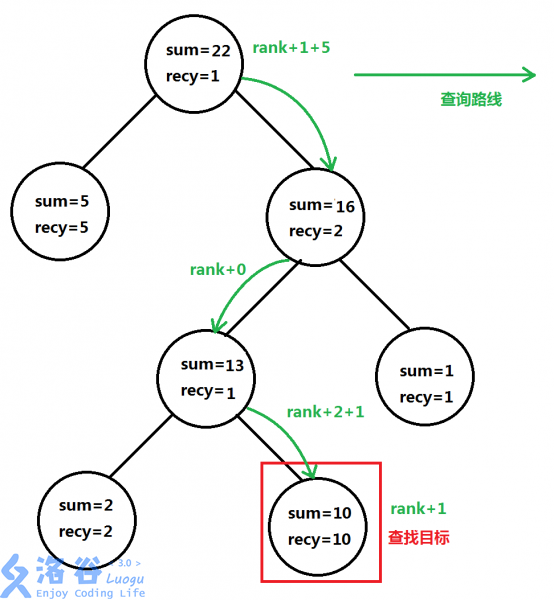
atrank函数根rank实现完全相反。在向下走的过程中,如果要找的排名大于当前点左子树的sum值,并且小于等于当前点的左子树的sum加上本节点的recy的值,那么当前的点就是要找的点。如果小于上述范围,就往左走,反之向右。注意向右走的过程中,将要查询的排名值减少上述范围的最大值。
两个操作结束后,都要将被操作的节点旋转到根。
int rank(int v)//获取值为v的元素在这棵树里是第几小
{
int ans=0,now=root;
while(true)
{
if(e[now].v==v) return ans+e[e[now].ch[0]].sum+1;
if(now==0) return 0;
if(v<e[now].v) now=e[now].ch[0];
else
{
ans=ans+e[e[now].ch[0]].sum+e[now].recy;
now=e[now].ch[1];
}
}
if(now) splay(now,root);
return 0;
}
int atrank(int x)//获取第x小的元素的值
{
if(x>points) return -INF;
int now=root;
while(true)
{
int minused=e[now].sum-e[e[now].ch[1]].sum;
if(x>e[e[now].ch[0]].sum&&x<=minused) break;
if(x<minused) now=e[now].ch[0];
else
{
x=x-minused;
now=e[now].ch[1];
}
}
splay(now,root);
return e[now].v;
}查找前驱(lower)和后继(upper)
两种操作是类似的操作。
前驱是指在树中,小于这个值并且最接近这个值的元素值。
后继则是大于这个值并且最接近这个值的元素值。
对于这两种函数的实现方式,就是先初始化一个最值,然后在向下走的过程中,如果发现了符合要求且更优的值,就用更优值替换当前的值。最后不能走的时候输出这个值即可。
int upper(int v)
{
int now=root;
int result=INF;
while(now)
{
if(e[now].v>v&&e[now].v<result) result=e[now].v;
if(v<e[now].v) now=e[now].ch[0];
else now=e[now].ch[1];
}
return result;
}
int lower(int v)
{
int now=root;
int result=-INF;
while(now)
{
if(e[now].v<v&&e[now].v>result) result=e[now].v;
if(v>e[now].v) now=e[now].ch[1];
else now=e[now].ch[0];
}
return result;
}完整源代码
下面贴出完整源代码,方便交流分享!
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 6 const int MAXL=100005; 7 const int INF=2147480000; 8 9 class Splay//存储规则:小左大右,重复节点记录 10 { 11 #define root e[0].ch[1] //该树的根节点 12 private: 13 class node 14 { 15 public: 16 int v,father;//节点值,父级节点 17 int ch[2];//左孩子=0,右孩子=1 18 int sum;//自己+自己下级有多少节点。在根节点为1。 19 int recy;//记录自己被重复了几次 20 }; 21 node e[MAXL];//Splay树主体 22 int n,points;//使用存储数,元素数 23 void update(int x) 24 { 25 e[x].sum=e[e[x].ch[0]].sum+e[e[x].ch[1]].sum+e[x].recy; 26 } 27 int identify(int x) 28 { 29 return e[e[x].father].ch[0]==x?0:1; 30 } 31 void connect(int x,int f,int son)//连接函数。用法:connect(son,father,1/0) 32 { 33 e[x].father=f; 34 e[f].ch[son]=x; 35 }//作用:使得x的father=f,f的son=x. 36 void rotate(int x) 37 { 38 int y=e[x].father; 39 int mroot=e[y].father; 40 int mrootson=identify(y); 41 int yson=identify(x); 42 int B=e[x].ch[yson^1]; 43 connect(B,y,yson);connect(y,x,(yson^1));connect(x,mroot,mrootson); 44 update(y);update(x); 45 } 46 void splay(int at,int to)//将at位置的节点移动到to位置 47 { 48 to=e[to].father; 49 while(e[at].father!=to) 50 { 51 int up=e[at].father; 52 if(e[up].father==to) rotate(at); 53 else if(identify(up)==identify(at)) 54 { 55 rotate(up); 56 rotate(at); 57 } 58 else 59 { 60 rotate(at); 61 rotate(at); 62 } 63 } 64 } 65 int crepoint(int v,int father) 66 { 67 n++; 68 e[n].v=v; 69 e[n].father=father; 70 e[n].sum=e[n].recy=1; 71 return n; 72 } 73 void destroy(int x)//pop后摧毁节点 74 { 75 e[x].v=e[x].ch[0]=e[x].ch[1]=e[x].sum=e[x].father=e[x].recy=0; 76 if(x==n) n--;//最大限度优化 77 } 78 public: 79 int getroot(){return root;} 80 int find(int v)//用于外部的find调用 81 { 82 int now=root; 83 while(true) 84 { 85 if(e[now].v==v) 86 { 87 splay(now,root); 88 return now; 89 } 90 int next=v<e[now].v?0:1; 91 if(!e[now].ch[next]) return 0; 92 now=e[now].ch[next]; 93 } 94 } 95 int build(int v)//内部调用的插入函数,没有splay 96 { 97 points++; 98 if(n==0)//特判无点状态 99 { 100 root=1; 101 crepoint(v,0); 102 } 103 else 104 { 105 int now=root; 106 while(true)//向下找到一个空节点 107 { 108 e[now].sum++;//自己的下级肯定增加了一个节点 109 if(v==e[now].v) 110 { 111 e[now].recy++; 112 return now; 113 } 114 int next=v<e[now].v?0:1; 115 if(!e[now].ch[next]) 116 { 117 crepoint(v,now); 118 e[now].ch[next]=n; 119 return n; 120 } 121 now=e[now].ch[next]; 122 } 123 } 124 return 0; 125 } 126 void push(int v)//插入元素时,先添加节点,再进行伸展 127 { 128 int add=build(v); 129 splay(add,root); 130 } 131 void pop(int v)//删除节点 132 { 133 int deal=find(v); 134 if(!deal) return; 135 points--; 136 if(e[deal].recy>1) 137 { 138 e[deal].recy--; 139 e[deal].sum--; 140 return; 141 } 142 if(!e[deal].ch[0]) 143 { 144 root=e[deal].ch[1]; 145 e[root].father=0; 146 } 147 else 148 { 149 int lef=e[deal].ch[0]; 150 while(e[lef].ch[1]) lef=e[lef].ch[1]; 151 splay(lef,e[deal].ch[0]); 152 int rig=e[deal].ch[1]; 153 connect(rig,lef,1);connect(lef,0,1); 154 update(lef); 155 } 156 destroy(deal); 157 } 158 int rank(int v)//获取值为v的元素在这棵树里是第几小 159 { 160 int ans=0,now=root; 161 while(true) 162 { 163 if(e[now].v==v) return ans+e[e[now].ch[0]].sum+1; 164 if(now==0) return 0; 165 if(v<e[now].v) now=e[now].ch[0]; 166 else 167 { 168 ans=ans+e[e[now].ch[0]].sum+e[now].recy; 169 now=e[now].ch[1]; 170 } 171 } 172 if(now) splay(now,root); 173 return 0; 174 } 175 int atrank(int x)//获取第x小的元素的值 176 { 177 if(x>points) return -INF; 178 int now=root; 179 while(true) 180 { 181 int minused=e[now].sum-e[e[now].ch[1]].sum; 182 if(x>e[e[now].ch[0]].sum&&x<=minused) break; 183 if(x<minused) now=e[now].ch[0]; 184 else 185 { 186 x=x-minused; 187 now=e[now].ch[1]; 188 } 189 } 190 splay(now,root); 191 return e[now].v; 192 } 193 int upper(int v)//寻找该值对应的一个最近的上界值 194 { 195 int now=root; 196 int result=INF; 197 while(now) 198 { 199 if(e[now].v>v&&e[now].v<result) result=e[now].v; 200 if(v<e[now].v) now=e[now].ch[0]; 201 else now=e[now].ch[1]; 202 } 203 return result; 204 } 205 int lower(int v)//寻找该值对应的一个最近的下界值 206 { 207 int now=root; 208 int result=-INF; 209 while(now) 210 { 211 if(e[now].v<v&&e[now].v>result) result=e[now].v; 212 if(v>e[now].v) now=e[now].ch[1]; 213 else now=e[now].ch[0]; 214 } 215 return result; 216 } 217 #undef root 218 }; 219 Splay F; 220 221 int main() 222 { 223 224 return 0; 225 }
后记
总算是讲完了如何实现最基础的Splay排序树。
可能会有大佬感觉:明明是来做题的了,怎么会有不懂Splay的呢?这不纯粹是装逼么?而且一点水平也没有,纯粹瞎扯淡!
我只能说,我刚开始学Splay的时候,就是一点一点的寻找相关资料的。包括从这道模板题找。但是系统讲解的还真没多少。而且贴出来的示例代码比较复杂,表示弱鸡看不懂。。。所以在钻研以后,写下了这篇文章。这些是我对Splay的理解。我将他们变成了书面的东西去分享给大家,希望大家能够从中受益,希望能够帮到更多正在努力学习平衡树的OIERS。如果有问题,也可以提出来,帮助我改进。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号