UVA12716 GCD XOR

题意翻译

输入数据组数t，接下来t行每行给定一个数字n，如样例所示格式输出满足1<=b<=a<=n且gcd(a,b)==a xor b的(a,b)二元组个数。

translated by @AdzearDisjudge

题目描述

PDF

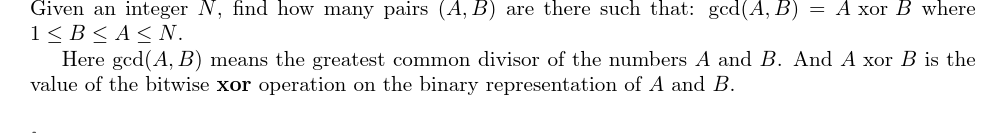
输入输出格式

输入格式：

 

 

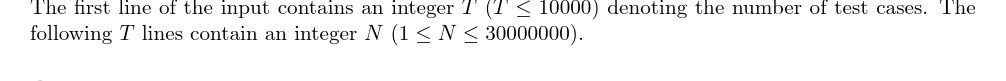
输出格式：

 

 

输入输出样例

输入样例#1： 

2
7
20000000

输出样例#1： 

Case 1: 4
Case 2: 34866117

 

Solution：

　　（又来补上博客…）本题应该是一次模拟考试的原题，思路很简单的数学。

　　我们假设$a>b$，不难得出结论：1、$a\;xor\; b\geq a-b$  2、$gcd(a,b)\leq a-b$。

　　先证明结论1：简单点说吧，异或操作可以看成凭空借位直接相减的减法（这里默认较大的数为被减数），比如说某位的运算为$0\;xor\;1$，并不需要向前一位借$1$而是直接将$0$加上$2$再减$1$得到运算结果为$1$。那么贪心的想到，$a\;xor\;b$的值一定会大于等于$a-b$的值，因为$a-b$运算时若某位不够减是向前一位借$1$而不是凭空借到$1$，或者理解成异或操作在某位不够减时被减数的该位凭空加上$2$，假设一次异或操作各数位上凭空借了的值的和为$c,c\geq 0$，显然就有$a+c-b\geq a-b$成立了。

　　再证明结论2：我们由欧几里得算法可知，$gcd(a,b)=gcd(b,a-b)$（该证明过于简单不需赘述），那么显然$a>b$时$gcd(a,b)\leq a-b$成立。

　　于是我们可以直接夹逼，设满足条件的$gcd(a,b)=a\;xor\;b=x$，则有$a-b\leq x\leq a-b$，那么显然$x=a-b$。

　　所以本题算法就出来了：考虑用前缀和统计方案数，直接$1\rightarrow n$枚举每个最大公约数$x$，然后判断相邻的两个$x$的倍数异或值是否为$x$，成立就前缀+1。

　　时间复杂度调和级数+询问T：$O(n\log n+T)$

代码：

 

/*Code by 520 -- 10.30*/
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define il inline
#define ll long long
#define RE register
#define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=3e7+5;
int s[N],T;

int gi(){
    int a=0;char x=getchar();
    while(x<'0'||x>'9') x=getchar();
    while(x>='0'&&x<='9') a=(a<<3)+(a<<1)+(x^48),x=getchar();
    return a;
}

int main(){
    For(g,1,N-1){
        for(RE int a=(g<<1),b=g;a<N;a+=g,b+=g) if((a^b)==g) s[a]++;
        s[g]+=s[g-1];
    }
    T=gi();
    For(i,1,T) printf("Case %d: %d\n",i,s[gi()]);
    return 0;
}