PCA主成分分析的推导和举例（附matlab代码）

尽量用最简洁的话，清晰讲述PCA的原理和过程

1.目的

降维。找到到一个维度，数据点在这个维度上的投影之间方差最大。

2.做法

假设现有矩阵X_m,n，即m个数据点，n个特征维度，想降到Z_m,k，即还是m个数据点，但此时每个数据只剩下k个维度了，此时k<m。那么翻译成数学语言就是，找到一个新的单位坐标W_n,k,使得

Z_m,k = X_m,n * W_n,k，

线性代数中，我们习惯将坐标系写到左边，数据点矩阵写到右边，即：

Z_k,m = W_k,n * X_n,m ，

简写：

 z = w*x;

求中X是原矩阵，w是新的单位正交坐标系，z是变换后的矩阵，还是那么多点，只是维度降低了，所以我们只要能把w求出来，再和原始矩阵x相乘就可以求出z了。那么怎么求w呢？

 

我们的原则是，此时在剩下的K个维度上（为了简单，可以先把k理解成1，即k = 1)，Z中的m个点之间方差最大，即:

 

又矩阵中A² = A*A^T,所以上式等价于 

 

<=> (带入z = wx)

 

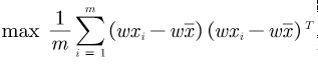
<=> (提出每个括号中的w) 

<=> （(AB)^T = B^TA^T）

 

 <=>

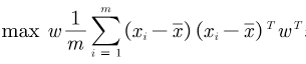
又因为x的方差S:

 

所以原式<=>

此时有个条件

 ||w||²  = 1，

这个可以理解为单位坐标系的模就是1，比如我们常用的直角坐标系x轴单位向量就是（1，0），y 轴单位向量就是（0，1），他们的模都是1 ，是单位向量。

解方程组

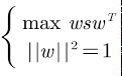
为了解方程组，构造拉格朗日函数 , 

<=>

 

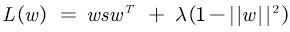
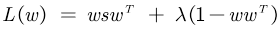
然后L对w求导，并让导数等于0，注意，矩阵求导中有写重要结论（图片来源于网络https://www.cnblogs.com/jiaxinwei/p/11450561.html）：

所以有：

 

即：

所以，λ是协方差矩阵S的特征值，而w就是λ所对应的特征向量。这就把所需要的w求出来了。那么回过头来

z= wx，w有了，x是原矩阵，所以降维后的矩阵z就可以求出来了。也就是我们需要求

的特征值和特征向量。然后求出来的特征向量就是新维度下的坐标系的单位向量，而每个特征向量所对应的特征值在所有特征值中所占的比例就是这个新的维度所占据的原始信息的程度大小，特征值越大说明这一维度越重要。

所以最重要的求PCA的步骤就出来了：

1，对原始数据矩阵求按维度求均值

2，对原始矩阵x按维度求协方差

3，对协方差矩阵求特征值特征向量，

4，选取较大的几个特征值所对应的特征向量组成新的矩阵w,用原始矩阵x乘以w就有了降维后的矩阵。

例如：

有一处卖房处，有五套房，房子面积和总房价组成了这些房子的连个维度，很明显，这俩个特征维度相关性太大，有冗余，所以我们想降维成一维的

房号	面积	价格
1	10	10
2	2	2
3	1	1
4	7	7
5	3	3

反映到二维坐标图上既是：

 

很明显我用二维有冗余，我们可以用一个如下的坐标系来表示：

 

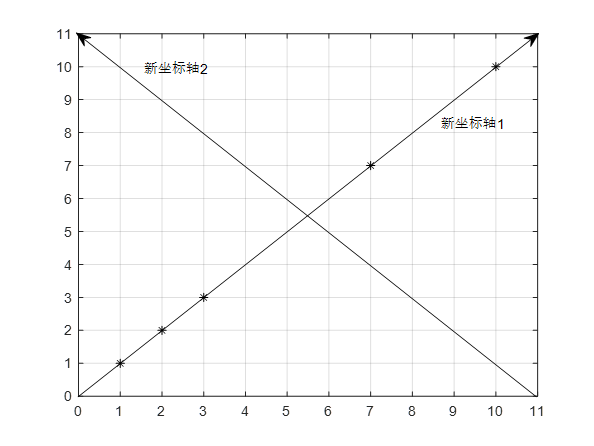
在这个新的坐标轴中，我们可以很明显的看出，只用“新坐标轴1”就可以完全概况出数据的特征，因为这些数据在坐标轴2中的没有投影值或者投影值很小，可以认为是噪声引起的，可以忽略。

直观的来讲，原始坐标系中，x轴单位坐标为e_x = [1;0]，y坐标轴的单位坐标为e_y =[0;1] (注意此处用分号表示换行）

这样才有了每个点的横坐标为X*e_x，纵坐标为X*e_y

X= [10    10

        2      2

       1       1

       7        7

       3        3]

横坐标 = X*ex

           =

 

 

 

 

 

=

 

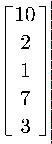
轴坐标 = X*ey

  =

 

=

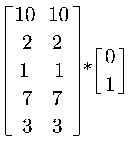
那么新的坐标系的单位横坐标应该是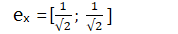

纵坐标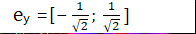

这样的话，原理几个点在新的坐标系下的坐标应该是

X*[e_x   e_y  ]

 =

 

 =

 

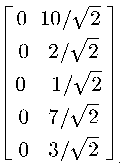
显然，在新坐标2这个维度中，所以坐标都为0，所以我们就可以把它降到了1维

 

这是数据较少，特征维数不多时候我们可以直观的看出来，那如果数据量成千上万，维度较多时候就不能直接看了，这就需要我们采用刚才PCA算法步骤去做了。

那么如果按照我们刚才PCA推导的算法是不是也是这个结果呢？接下来就按照结论中的流程走一遍，

具体做法就是，首先求每个维度的均值：

A = [10 2 1 7 3]';

A1 = A-mean(A);

A2 = A-mean(A);

oldA = [A A]；

newA = [A1 A2];

得到

oldA =

 

    10    10

     2     2

     1     1

     7     7

     3     3

 

newA =

 

    5.4000    5.4000

   -2.6000   -2.6000

   -3.6000   -3.6000

    2.4000    2.4000

   -1.6000   -1.6000

 

然后求协方差矩阵

Q = newA'*newA;

得到

Q =

 

   57.2000   57.2000

   57.2000   57.2000

再求Q的特征值和特征向量：

[X Y] = eig(Q)

得到

X =

 

   -0.7071    0.7071

    0.7071    0.7071

 

 

Y =

 

         0         0

         0  114.4000

此时我们看到,Q的特征值为0和114.4，那么114.4最大，所对应的特征向量【0.7071；0.7071】得以保留，成为新的单位坐标向量w,即w = X（：，2） = [0.7071；0.7071]

用w 和原始矩阵相乘就得到了降维后的矩阵：

newAA = oldA*X(:,2)

得到：

newAA =

 

 10*2^(1/2)

  2*2^(1/2)

    2^(1/2)

  7*2^(1/2)

  3*2^(1/2)

 和我们直观的手算结果一样！

此时我们最好是用减去均值后的矩阵进行降维，因为这样可以将原始坐标维度原点都转至维度中心，即：

newAA = newA*X(:,2)

得到

newAA =

 

    7.6368

   -3.6770

   -5.0912

    3.3941

   -2.2627

 

可以验证一下，

P = X*Y*X'

DQ = Q-P

 得到：

P =

 

   57.2000   57.2000

   57.2000   57.2000

 

DQ =

 

   1.0e-14 *

 

    0.7105    0.7105

 

完整代码：
clear
clc
close all
A = [10 2 1 7 3]'
% B = [9 3 2 6.5 2.5]'
mA = mean(A)
nmA = A-mA
A1 = nmA
A2 = nmA
oldA = sym([A A])
newA = [A1 A2]
Q = newA'*newA
[X Y] = eig(Q)
ori = [0 0]';
xlnew = 10*[ori,X(:,2)]
ylnew = 10*[ori,X(:,1)]
sizeA = size(newA)
figure
plot(oldA(:,1),oldA(:,2),'k*');
xlim([0 11])
ylim([0 11])
grid on
figure
hold on
plot(newA(:,1),newA(:,2),'k*');
plot(xlnew(1,:),xlnew(2,:))
plot(ylnew(1,:),ylnew(2,:))
grid on
% ylim([-0.8 0.8])
newAA = oldA*X(:, 2)
newAA = newA*X(:, 2)
P = X*Y*X'
DQ = Q-P