计蒜客练习题：两仪剑法

lcm和gcd练习题：两仪剑法

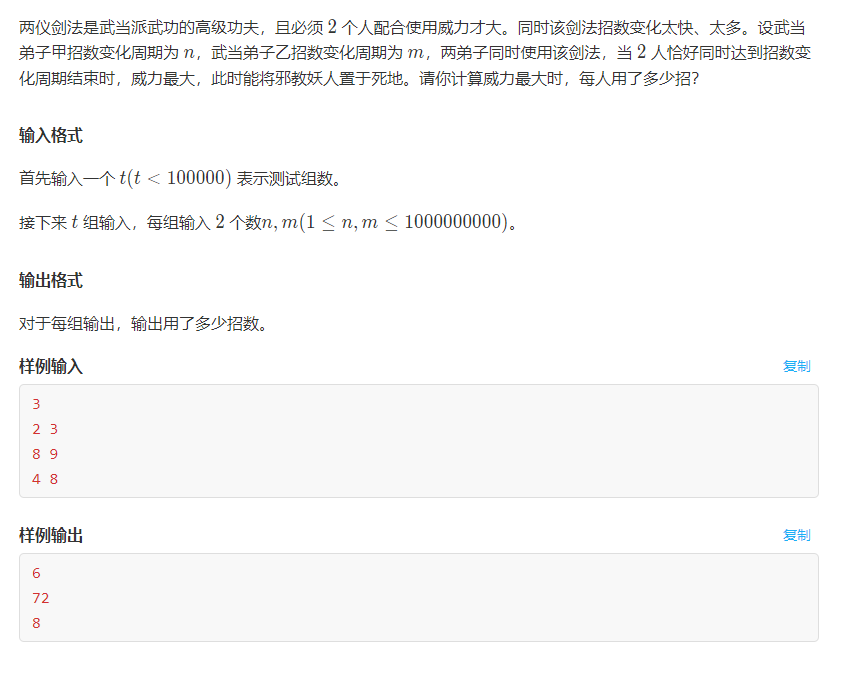
解题：就是求最小公倍数lcm：可以先用__gcd算出最大公约数，根据gcd与lcm的性质公式：gcd * lcm = a * b算出lcm。

注意：数据n和m最大为10亿，需使用long long型。

AC代码：

#include<algorithm>
#include<iostream>
using namespace std;

int gcd(int a,int b){
	if(b==0){
		return a;
	}
	return gcd(b,a%b);
}


int main(){
	int t; 
	long long n,m;
	cin>>t;
	while(t--){
		cin>>n>>m;
		cout<<n /gcd(n,m) * m<<endl;
	}
} 

方法二：辗转相减法求最大公约数，再求最小公倍数（时间复杂度更小）

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

//辗转相减法 求最大公约数
long long int measure(int a,int b)  
{         
    while(a != b)  
    {  
        if(a>b)  
        {  
            a = a - b;  
        }  
        else   
        {  
            b = b - a;  
        }  
    }  
    return a; 
}  
int main ()
{
  long long int n;
  cin>>n;
  while(n--)
  {
    long long int n,m;
    scanf("%lld %lld",&n,&m);
    printf("%lld\n",(n*m)/measure(n,m));
  }
  return 0 ;
}