LeetCode 单调栈专题
单调栈
单调栈应用场景及模板
应用场景:“找最接近某个元素”的最值问题
如:查找每个数左边第一个比它小的数;
再如:查找每个数右边第一个比它大的数;等等
洛谷P5788 【模板】单调栈
题意:找每个数右侧第一个大于它的数
两种写法:正序或者倒序;
正序:从0~n-1,对于当前元素i,每次弹出已在栈中的(位于i左侧)比i小的元素;那么这些被弹出的元素右侧第一个大于它的数就是元素i了;即出栈的时候记录答案;
最终栈中永远只保持单调递减,因为比当前元素i小的都弹出了,剩下的左侧都是比i大的数
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
const int maxn = 3e6+100;
ll a[maxn];
int stk[maxn];
ll result[maxn];
int top = 0;
/*
正序 找右边第一个大的数
单调栈中总保持递减 小的都出栈 它们的答案被标记为当前元素
*/
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=n;i++){
while(top>0 && a[stk[top]] < a[i]){ //注意是小于 不是 大于等于
result[stk[top]] = i;
top--;
}
stk[++top] = i;
}
for(int i=1;i<=n;i++) printf("%d ",result[i]);
return 0;
}
/*
5
1 4 2 3 5
*/
倒序:从n-1到1;找右边第一个大的数 ;把从元素i右侧(已经在栈中)小的都出栈;直到遇到栈中第一个比i对应a[i]大的数;小的都出栈后,最后栈顶就对应了i右侧第一个比它大的数。需要判断栈顶是不是为空。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
const int maxn = 3e6+100;
ll a[maxn];
stack<int> stk;
ll result[maxn];
/*
找右边第一个大的数
从后往前 小的都出栈 直到遇到栈中第一个比i对应a[i]大的
就是向右边看的第一个最大
*/
int main() {
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=n;i>=1;i--){
while(!stk.empty() && a[stk.top()] <= a[i]){
stk.pop();
}
if(stk.empty()) result[i] = 0;
else result[i] = stk.top();
stk.push(i);
}
for(int i=1;i<=n;i++) cout<<result[i]<<" ";
return 0;
}
/*
5
1 4 2 3 5
*/
739. 每日温度
找右边第一个比当前大的元素位置,与当前i的距离
即单调栈中是单调递减序列
(进来一个新元素i小的都被弹出栈,出栈的过程中小的最大值答案都是当前位置i)
这种情况下要考虑栈中剩余的元素
倒序从右向左,
class Solution {
public:
stack<int> stk;
vector<int> result;
int n;
vector<int> dailyTemperatures(vector<int>& T) {
n = T.size();
result = vector<int>(n);
for(int i=n-1;i>=0;i--){
//右边小于等于它的都出栈 剩下的肯定都是大于它的
while(!stk.empty()
&& T[stk.top()] <= T[i]) stk.pop();
//特判栈顶是不是空
//若不空,当前i对应的答案就是栈顶(第一个大的)
if(stk.empty()) result[i] = 0;
else result[i] = stk.top() - i;
stk.push(i);
}
return result;
}
};
正序从左向右:
class Solution {
public:
stack<int> stk;
vector<int> result;
int n;
vector<int> dailyTemperatures(vector<int>& T) {
n = T.size();
result = vector<int>(n);
for(int i=0;i<n;i++){
//左边(已在栈中)小于当前元素的都出栈 当前i就是它们的答案
while(!stk.empty() && T[stk.top()] < T[i]) {
result[stk.top()] = i - stk.top();
stk.pop();
}
//剩下的都是大于等于当前元素 栈中总保持单调递减
stk.push(i);
}
while(!stk.empty()){
result[stk.top()] = 0;
stk.pop();
}
return result;
}
};
84. 柱状图中最大的矩形
枚举位置,用这个位置的上边界数值作为对象
1.找到左边最近的第一个比当前值小的位置下标
2.找到右边最近的第一个比当前值小的位置下标
算出宽度,边界作为长;面积就是 长 × 宽
用两遍单调栈维护,从左边开始比它小的;再维护一遍从右边开始比它小的


class Solution {
public:
int n;
int ans;
stack<int> stk;
vector<int> left,right;
//1.从左向右找第一个比它小的
//2.从右向左找第一个比它小的
int largestRectangleArea(vector<int>& heights) {
n = heights.size();
left = vector<int>(n),right = vector<int>(n);
ans = 0;
for(int i=0;i<n;i++){
//左边(已经在栈中) 大于等于i的都出栈
//最终栈首它左边留下第一个小于它的
while(!stk.empty() &&
heights[stk.top()] >= heights[i]){
stk.pop();
}
if(stk.empty()) left[i] = -1;
else left[i] = stk.top();
stk.push(i);
}
while(stk.size()) stk.pop();
for(int i=n-1;i>=0;i--){
//右边(已经在栈中) 大于等于当前i的都出栈
//最终栈首留下右边第一个小于它的
while(!stk.empty() &&
heights[stk.top()] >= heights[i]){
stk.pop();
}
if(stk.empty()) right[i] = n;
else right[i] = stk.top();
stk.push(i);
}
for(int i=0;i<n;i++)
ans = max(ans,((right[i] - 1) - (left[i] + 1) + 1 ) * heights[i]);
return ans;
}
};
42. 接雨水
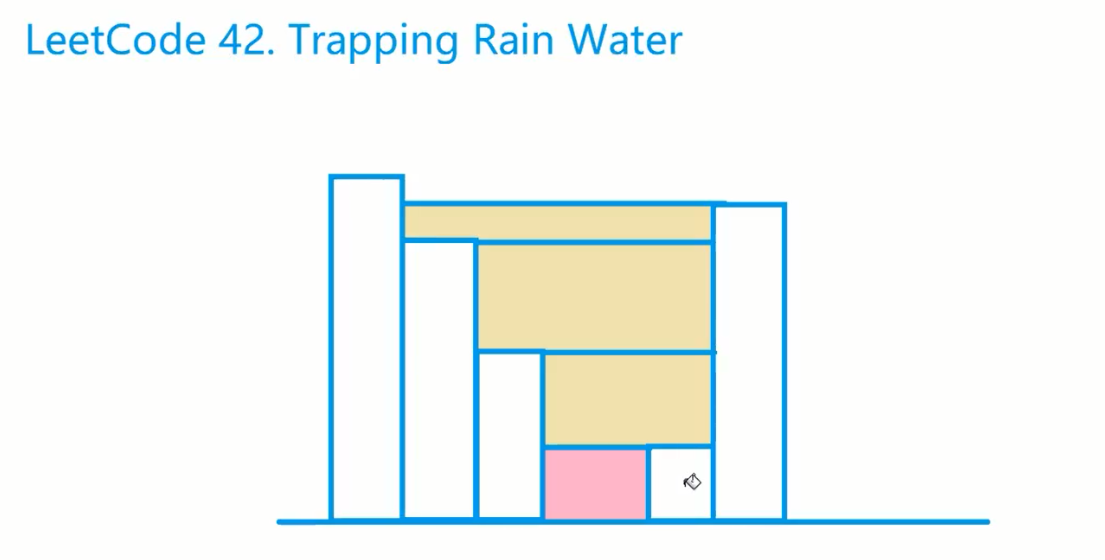
可以这样来思考:新来一个柱子增加的面积是多少?就是它与左侧第一个比它大的柱子之间的这段空间的面积。
那么这段空间的面积如何计算?可以从当前柱子开始依次向左考虑增加的面积;
左边遇到一个比它高度小的,增加的面积就是 (高-上一个比他小的) * 宽度,对应上图橙色区域
即新来一个柱子,移除左边比它小的柱子,直到找左侧比它大的柱子;
每次移除小柱子时,计算与前一个小柱子的高度差作为长;距离新柱子的距离作为宽。新增加面积就是长×宽
1.一层一层加面积,找到左边第一个比它大的元素。
在线更新:在单调栈出栈更新的时候(即左边柱子比它小得时候)的过程中加面积
2.最后再加上自己水平到比他大的一个矩形
class Solution {
public:
int n;
stack<int> stk;
//新来一个柱子i 找它左边第一个比它大的柱子 其它小的柱子在出栈的过程中更新
int trap(vector<int>& height) {
n = height.size();
int ans = 0;
for(int i=0;i<n;i++){
int lastHeight = 0;
//把左侧比当前i高度小的都出栈
//栈的过程中更新last高度 计算这次面积
while(!stk.empty() &&
height[stk.top()] <= height[i]){
//求宽高 计算柱子i与它左侧top柱子的面积
int weight = i - stk.top() - 1;
int high = height[stk.top()] - lastHeight;
ans += high * weight;
lastHeight = height[stk.top()];
stk.pop();
}
if(!stk.empty()){ //加上自己与左侧第一个比它高的面积
ans += (height[i]-lastHeight) *
(i - stk.top() - 1);
}
stk.push(i);
}
return ans;
}
};


