LeetCode DFS搜索与回溯专题

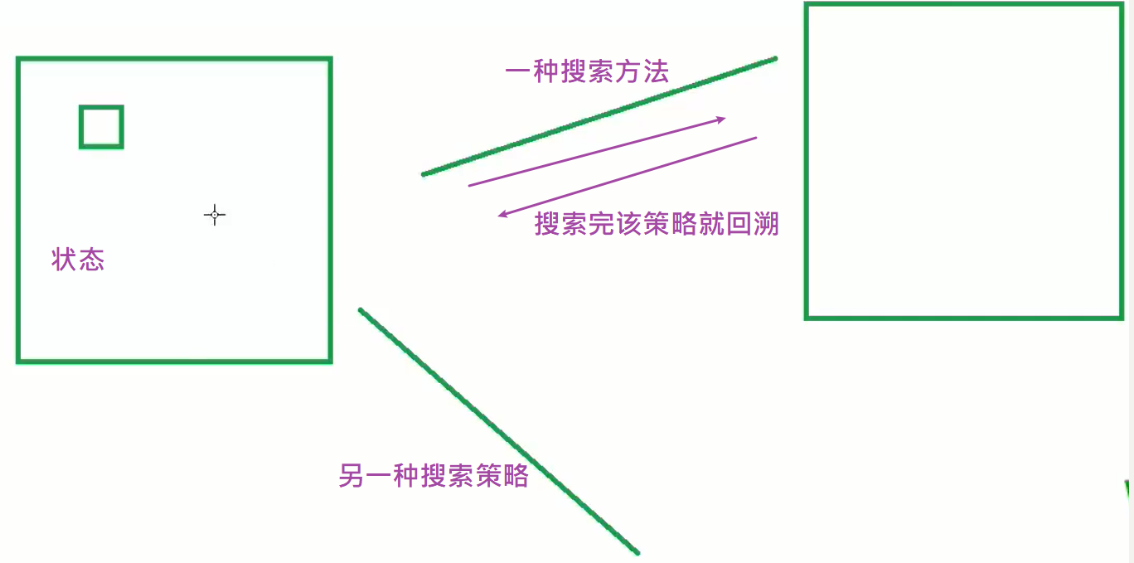
DFS + 回溯专题

17. 电话号码的字母组合

迭代也可以实现搜索

循环改写dfs搜索的写法：

例如

C++写法

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        string alp[8] = {"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
        vector<string> state;
        if(digits.empty()) return state;
        state.push_back("");
        for(int i=0;i<digits.size();i++){
            char number = digits[i];
            vector<string> now;
            for(int j=0;j<alp[number-'2'].size();j++){
                char ch = alp[number-'2'][j];
                for(int k = 0;k < state.size();k++){
                    now.push_back(state[k] + ch);
                }
            }
            state = now;
        }
        return state;
    }
};

C++11+ forEach遍历，新语法写法

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        string alp[8] = {"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
        vector<string> state;
        if(digits.empty()) return state;
        state.push_back("");
        for(auto digit : digits){ //对digits进行遍历 取得每一个按键数字
            vector<string> now;
            for(auto c : alp[digit - '2']){ //对数字对应的string能表示的形式遍历
                for(auto s : state){ //对state集合里的状态进行遍历
                    now.push_back(s + c);
                }
            }
            state = now;
        }
        return state;
    }
};

两种写法耗时对比：

79. 单词搜索

搜索题

考虑顺序：

1.枚举起点 n×m

2.从起点开始依次搜索下一个点的位置 上下左右走3种

3.在枚举的过程中要保证和目标单词匹配

时间复杂度 n×m × 3^k，k为单词字符串word的长度

class Solution {
public:
    int n,m;
    int dx[4] = {1,-1,0,0},dy[4] = {0,0,-1,1}; //上下左右4个方向
    bool exist(vector<vector<char>>& board, string word) {
        if(board.empty()  || board[0].empty())  return false;
        n = board.size(),m = board[0].size();
        for(int i=0;i<n;i++){ //1.枚举起点(第一个字符向匹配的点)
            for(int j=0;j<m;j++){
                if(dfs(board,i,j,word,0)) return true; //2.从起点开始搜索
            }
        }
        return false;
    }

    bool dfs(vector<vector<char>>& board,int x,int y,string word,int k){
        if(board[x][y] != word[k]) return false;
        //递归出口 当最后一个字符到达
        if(k == word.size() - 1) return true; 
        board[x][y] = '.'; //标记已访问过 用过
        for(int i=0;i<4;i++){ //枚举4个方向
            int nx = x + dx[i],ny = y + dy[i];
            if(nx >= 0 && nx < n && ny >=0 && ny < m){
            	//递归搜索单词的下一个字符
                if(dfs(board,nx,ny,word,k+1)){ 
                    return true;
                }
            }
        }
        board[x][y] = word[k]; //回溯
        return false;
    }
};

46. 全排列

全排列，先考虑顺序问题，不能重复

全排列有两种方案

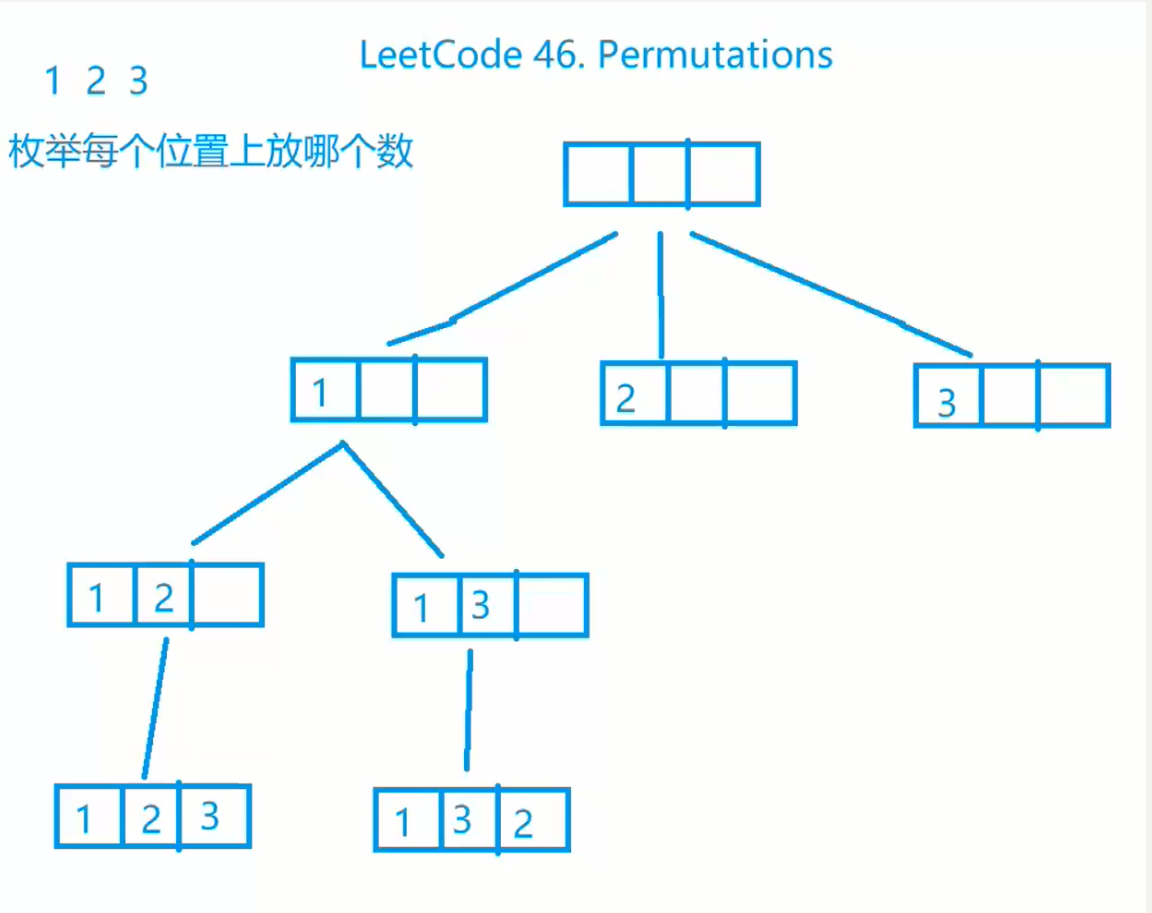
第一种方案，枚举每个位置上放哪个数字，每次dfs搜索时枚举这个数标记、回溯

class Solution {
public:
    int n;
    vector<bool> vis;
    vector<int> path;
    vector<vector<int> > result;

    vector<vector<int>> permute(vector<int>& nums) {
        n = nums.size();
        vis = vector<bool>(n,false); //初始化bool容器
        dfs(nums,0);
        return result;
    }
	
	//枚举第k个数该放哪个数字 即枚举数字
    void dfs(vector<int>& nums,int k){
        if(k == n){
            result.push_back(path);
            return;
        }
        //枚举当前第k个位置上该放哪个数字 枚举这个数字的下标
        for(int i=0;i<n;i++){ 
            if(!vis[i]){
                vis[i] = true; //标记用过
                path.push_back(nums[i]); //放入这个数
                dfs(nums,k+1);
                path.pop_back(); //回溯
                vis[i] = false;
            }
        }
    }
};

47. 全排列 II

与leetcode46比较，这题数字可能重复

需要判重

A.采用枚举每个数在哪个位置
B.判重的思路：

1.对nums数组进行排序

2.dfs搜索的时候需要保证值相同的数不在同一个位置上(从下一个位置开始)搜索

class Solution {
public:
    int n;
    vector<vector<int>> result;
    vector<int> path;
    vector<bool> visit;

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        n = nums.size();
        visit = vector<bool>(n);
        path = vector<int>(n);

        sort(nums.begin(),nums.end());

        dfs(nums,0,0);

        return result;
    }

    //对一个数枚举该放哪个位置  即枚举位置
    void dfs(vector<int>& nums,int k,int start){
        if(k == n){ //递归出口
            result.push_back(path);
            return;
        }
        //枚举num[k]放的位置在哪
        for(int i=start;i<n;i++){ //从start开始枚举
            if(!visit[i]){
                visit[i] = true;
                path[i] = nums[k];
            //去重关键: 
			//对相邻重复元素枚举的位置从下一个位置开始 而不从0开始
                if(k+1 <n && nums[k+1] == nums[k]){ 
                    dfs(nums,k + 1,i+1);
                }else{
                    dfs(nums,k + 1,0);
                }
                visit[i] = false;
            }
        }
    }
};

78. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

递归考虑顺序：按顺序，枚举每个数两种状态：选、不选

方法一：dfs

class Solution {
public:
    int n;
    vector<int> path;
    vector<vector<int>> result;
    vector<vector<int>> subsets(vector<int>& nums) {
        n = nums.size();
        dfs(0,nums);
        return result;
    }
    void dfs(int k,vector<int>& nums){
        if(k == n){
            result.push_back(path);
            return;
        }
        dfs(k+1,nums);
        path.push_back(nums[k]);
        dfs(k+1,nums);
        path.pop_back();
    }
};

方法2：二进制枚举：i从0到2^n-1，位置上是1的时候选，0的时候不选

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> result;
        //二进制枚举 每个数代表一种方案
        for(int i=0;i< 1<<nums.size() ;i++){ 
            vector<int> now;
            //枚举每一位 位数一共nums.size()
            for(int j=0;j<nums.size();j++){ 
                //如果第j位上数字为1就表示选这个数
                if(i >> j & 1){ 
                    now.push_back(nums[j]);
                }
            }
            result.push_back(now);
        }
        return result;
    }
};

90. 子集 II

与leetcode78的区别：数字可以重复

枚举的时候，再枚举这个数的选多少个

class Solution {
public:
    int n;
    vector<vector<int>> result;
    vector<int> path;
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        n = nums.size();
        sort(nums.begin(),nums.end()); //先排序
        dfs(nums,0);
        return result;
    }
    void dfs(vector<int>& nums,int k){
        if(k == n){
            result.push_back(path);
            return;
        }

        //统计后面与当前元素相同的个数
        int cnt = 0; 
        while(k + cnt < n && nums[k + cnt] == nums[k]) cnt++;

        for(int i=0;i<=cnt;i++) {
            dfs(nums,k + cnt);
            path.push_back(nums[k]);
        }
        for(int i=0;i<=cnt;i++) path.pop_back();
    }
};

216. 组合总和 III

找出所有相加之和为 n 的 k个数的组合

组合中只允许含有 1 - 9 的正整数

并且每种组合中不存在重复的数字。

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    vector<vector<int>> combinationSum3(int k, int n) {
        dfs(k,1,n);
        return result;
    }

    //当前还剩k个没选  选到了数字start上  总和还需要n
    void dfs(int k,int start,int n){
        if(k == 0){
            if(n == 0) result.push_back(path);
            return;
        }
        for(int i = start; i <= 9; i++ ){
            path.push_back(i);
            //剩k-1个没选 选到i+1了 总和还需要n-i
            dfs(k-1,i+1,n-i);
            path.pop_back();
        }
    }
};

剪枝：因为还需要选k个，i<=9即最大值可以替换为 i<=9 + 1 - k个

for(int i = start; i <= 10-k; i++ )

52. N皇后 II

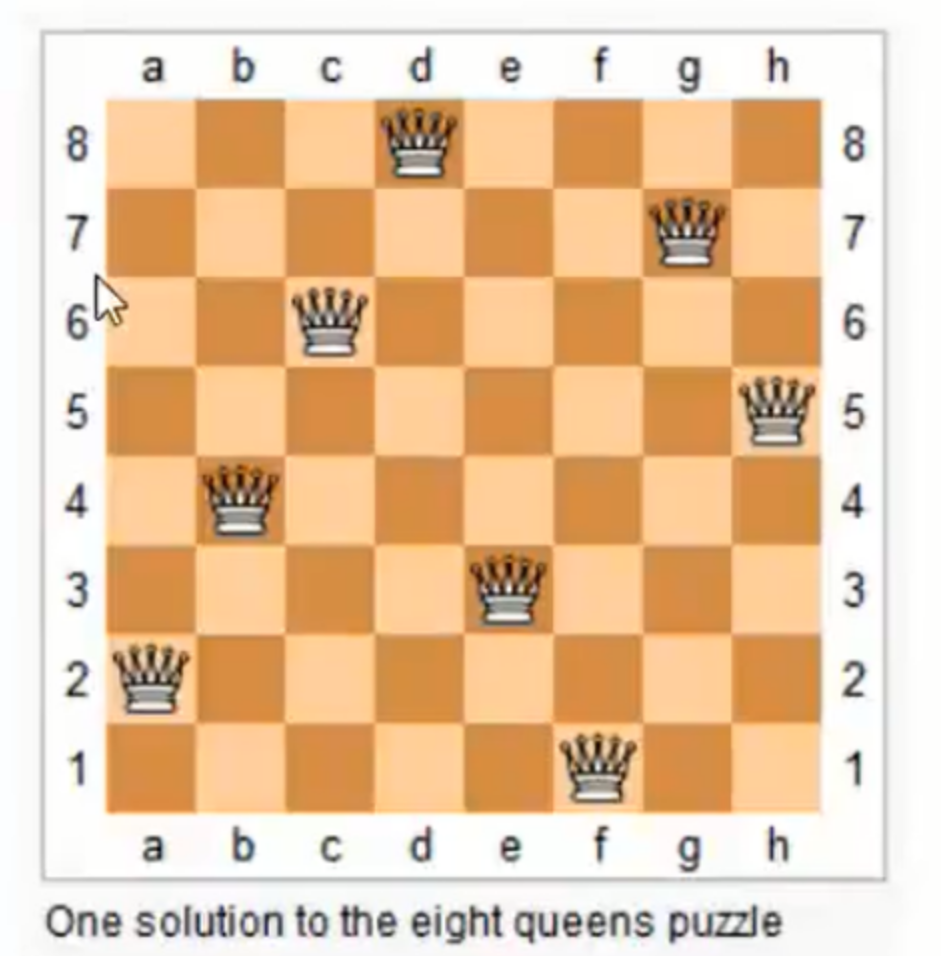
方法一：枚举每一个坐标放不放棋子

class Solution {
public:
    int ans;
    vector<bool> col,row,diag,anti_diag;
    int totalNQueens(int n) {
        row = col = vector<bool>(n,false);
        diag = anti_diag = vector<bool>(2*n,false);
        ans = 0;
        dfs(0,0,0,n);
        return ans;
    }

    //当前搜索到的坐标x,y  当前已选择的皇后个数  
    void dfs(int x,int y,int k,int n){
        if(y == n) x++, y = 0;
        if(x == n){
            if(k == n) ans++;
            return;
        }
        dfs(x,y+1,k,n); //不选这个位置
        if(!row[x] && !col[y] && !diag[x+y] && !anti_diag[n+x-y]){
            row[x] = col[y] = diag[x+y] = anti_diag[n+x-y] = true;
            dfs(x,y+1,k+1,n);
            row[x] = col[y] = diag[x+y] = anti_diag[n+x-y] = false;
        }

    }
};

方法二：枚举每一行放在哪个位置，只需枚举行

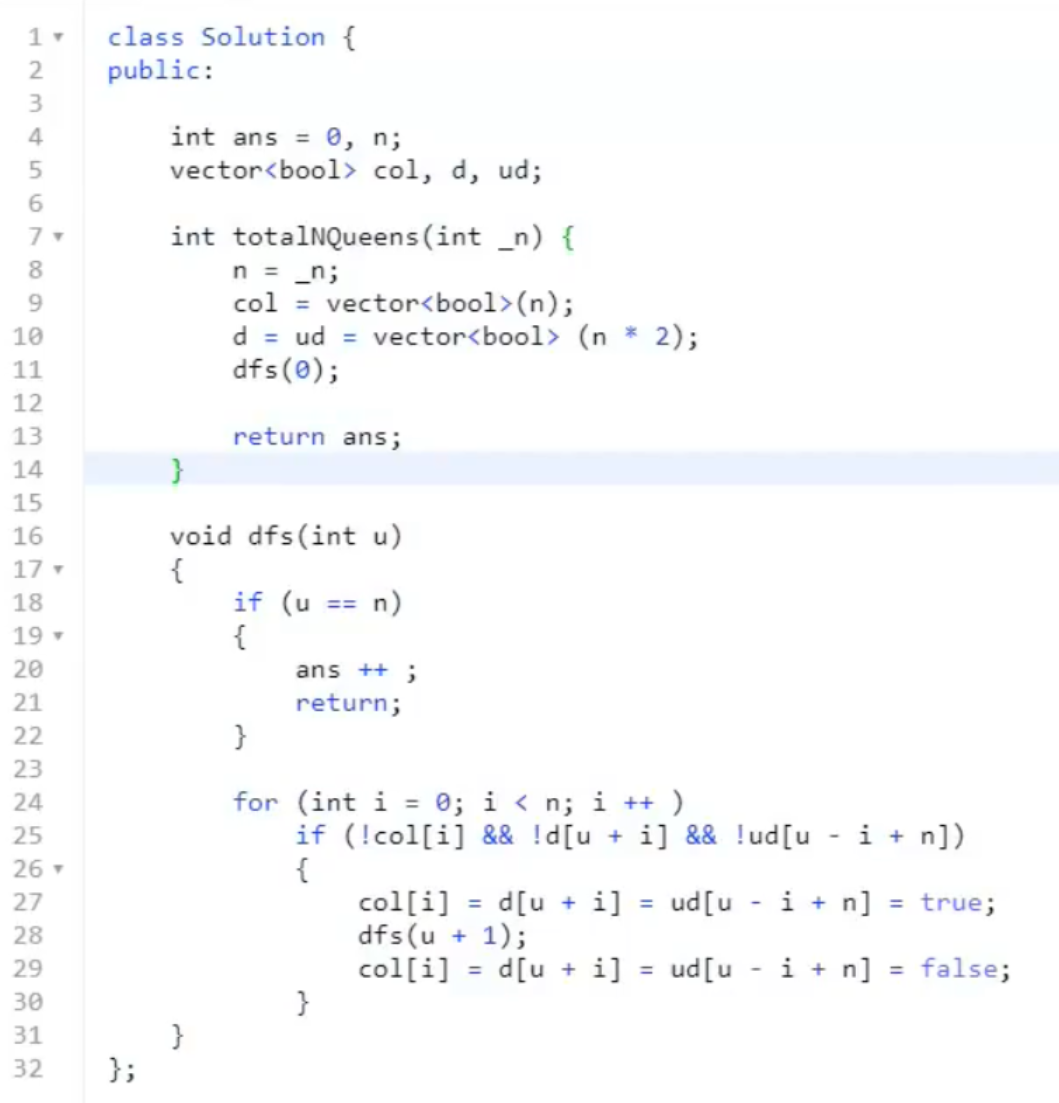
37. 解数独

开三个标记数组，分别标记行、列、所在九宫格是否用过某个数

1.先初始化，统计原棋盘已经放的元素。

2.dfs搜索每一个坐标点，枚举该坐标点下能放哪个数字，要求所在行、所在列、所在九宫格都没有这个数字，

3.递归下一个子节点，递归完true就结束程序；否则回溯这个点

52和37的小结：

Dancing Links解决 精确覆盖问题

十字链表

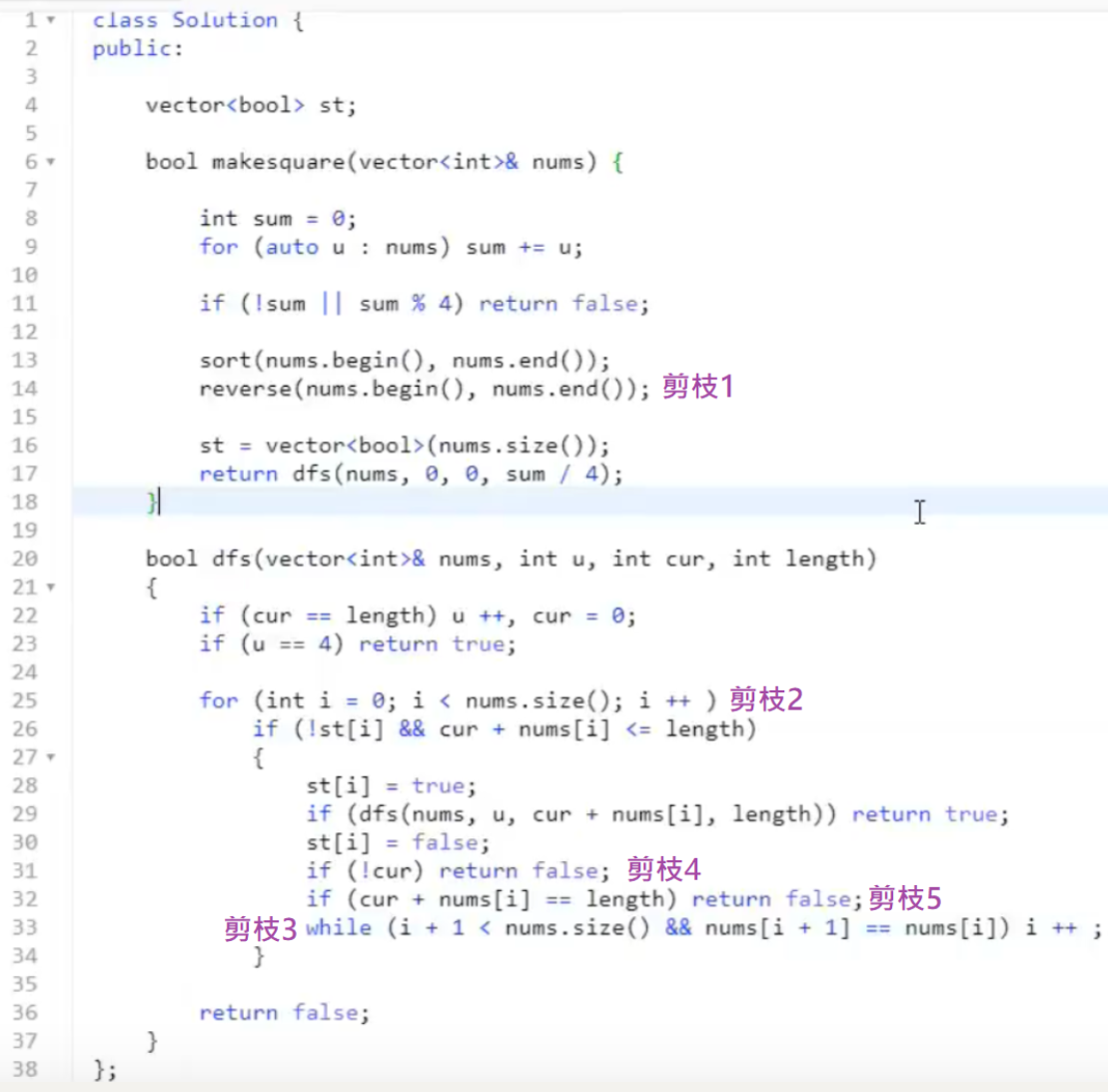
473. 火柴拼正方形

剪枝优化题

超时代码：时间复杂度n^4

class Solution {
public:
    int n;
    int ave;
    vector<bool> vis;
    bool makesquare(vector<int>& nums) {
        n = nums.size();
        vis = vector<bool>(n,false);
        sort(nums.begin(),nums.end());
        reverse(nums.begin(),nums.end());
        long long sum = 0;
        int cnt = 0;
        for(int i=0;i<n;i++){
            sum += nums[i];
        }
        if(sum == 0 || sum % 4 != 0 ) return false;
        for(int i=0;i<n;i++){
            if(nums[i] > sum/4) return false;
            if(nums[i] == sum/4) {
                cnt++;
                vis[i] = true;
            }
        }
        if(cnt == 4 && n == 4) return true; 
        for(int i=0;i<n;i++){
            if(nums[i] >= sum/4) continue;
        }
        ave = sum/4;
        return dfs(4-cnt,0,nums);
    }

    bool dfs(int k,int ans,vector<int>& nums){
        if(k == 0){ //递归出口
            for(int i=0;i<n;i++){
                if(!vis[i]) return false;
            }
            return true;
        }
        if(ans > ave) return false; //剪枝

        if(ans == ave) return dfs(k-1,0,nums); 
        //枚举这一轮选的数
        for(int i=0;i<n;i++){
            if(vis[i]) continue;
            vis[i] = true;
            if(dfs(k,ans+nums[i],nums)) return true;
            vis[i] = false;
        }
        return false;
    }
};

剪枝优化代码：