CF-div2-633-C - Powered Addition

思路

枚举幂x，加2^x，加到比前面最大值即可，
因为前x-1个一定能凑出最大值。(前x-1一定能凑出任意比它小的数)

比如，5 1； 5 > 1 + 2^3；那么前2个一定能凑到5，1 + 4 = 5；
再如，17 6； 17 > 6 + 2^4 那么前3个一定能凑到17，17与6差值为11，11 = 1011(二进制)，那么选2^0 + 2^1 +2^3 = 11;
再如，17 0；17 > 0 + 2^5 那么前4个选一部分累加一定能凑到17，17与0的差值位17，17 = 10001(二进制)，那么选2^0 + 2^4 = 17;

这因为二进制的性质，能凑出任意比它最高位少的数。

下图构造出17

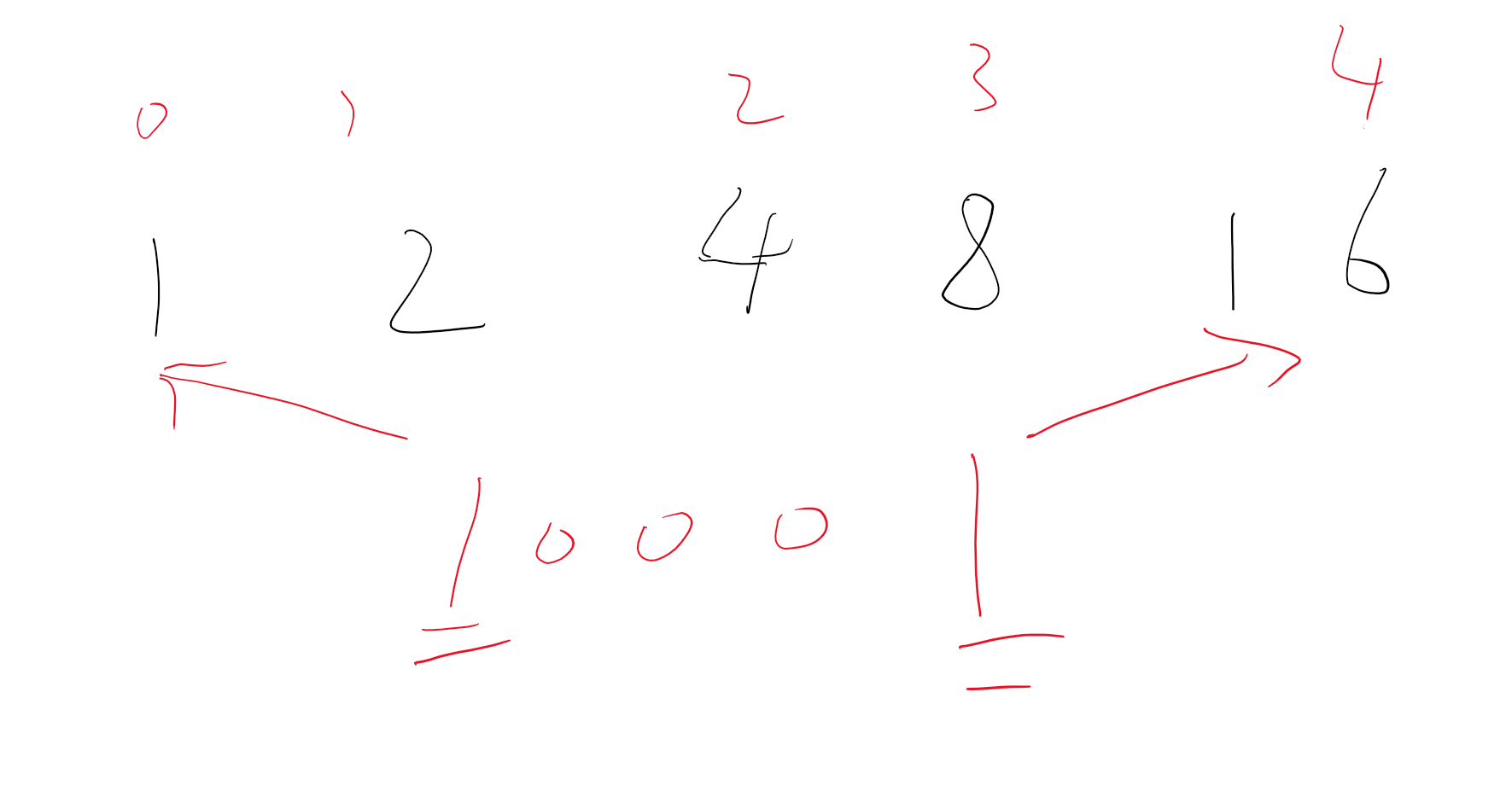
代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll; 

const int maxn = 1e5+100;
int t;
int n;
ll a[maxn];

void solve(){
	cin>>n;
	for(int i = 1;i<=n;i++) cin>>a[i];
	ll maxc = a[1]; //maxc记录前面的最大值 
	int ans = 0;
	for(int i=2;i<=n;i++){
		if(a[i] < maxc){ //a[i]比maxc小 才考虑增大ai;比maxc大肯定就不考虑增加它了 
			int x = 0;
			for(int j=0;j<=31;j++){
				if(a[i] + pow(2,j) > maxc){ //能加到比maxc大 
					x = j;
					break;
				}
			}
			ans = max(ans,x); //前x次(不包含x)一定能凑出与maxc相等的值
		}
		maxc = max(a[i],maxc);
	} 
	cout<<ans<<endl;
}

int main(){
	cin>>t;
	while(t--){
		solve();
	}
	return 0;
}