详细题解|蓝桥杯第十一届软件类校内模拟赛
大纲:
1.GB*1024=MB 答案:15488
2.枚举约数,答案:96
3.完全二叉树最多,答案:1010(不知道有没有看错题,是不是二叉)
4.枚举,判是否包含9,544
5.50%数据:3层枚举判递增;100%数据:思路1,枚举中心点,查左边<i的,查右边>i的,总时间复杂度O(n^2);思路2:查询可以优化,用树状数组查,总时间复杂度O(longn)
6.100%数据:枚举,倒着判数字是否递减,O(10^7) 不会超时
7.100%数据:字符串模拟
8.70%数据:按题意模拟,更新原草地;100%数据:思路1,bfs搜索;思路2:二维差分
9.50%数据:dfs暴力搜索;80%数据:记忆化搜索;100%数据:记忆化搜索+打表。
10.60%数据:按题意模拟,每次查询前一个元素后面的元素的最大值;时间复杂度O(n^2);100%数据:思路1:按60%的思路中的查询可以用线段树优化,用线段树查询区间最大值,时间复杂度O(nlongn)
下面是详细代码和大题按数据点给分的各个思路:
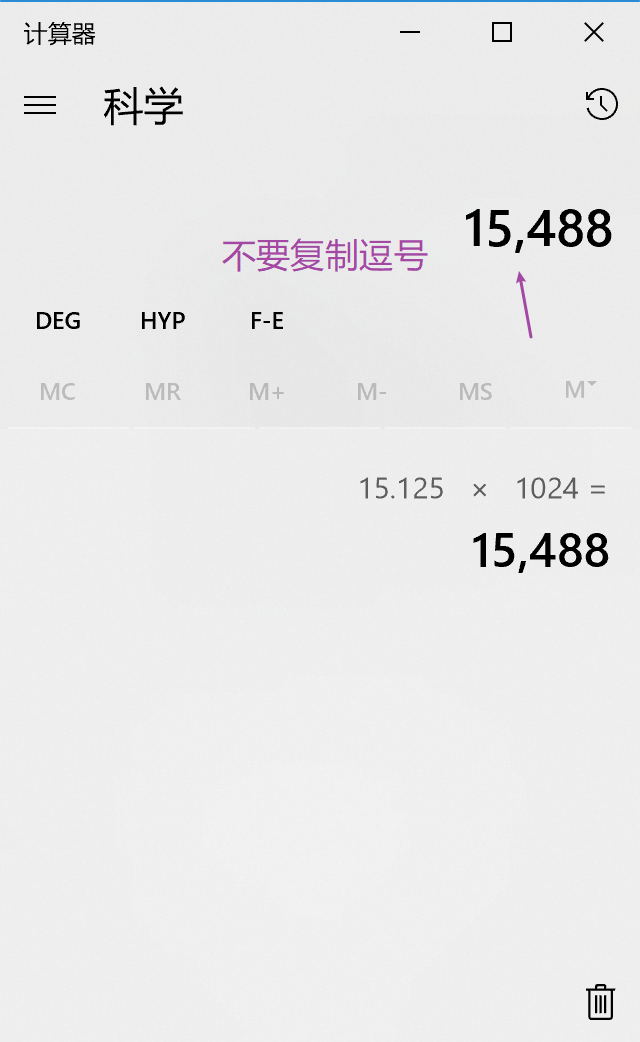
1. 答案:15488
15.125GB*1024 = 15488MB,用计算器算一下,答案是15488
2. 答案:96
1200000有多少个约数(只计算正约数)。
枚举1200000的约数,set去重
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6+10;
set<int> se;
int main(){
ll x = 1200000;
for(ll i = 1; i <= sqrt(x); i++){
if(x%i == 0) {
se.insert(i);
se.insert(x/i);
}
}
cout<<se.size();
return 0;
}
3. 答案:未知
一棵包含有2019个结点的树,最多包含多少个叶结点?
不记得是不是二叉树了,如果是一颗普通的树,那么答案是2018;
如果是一个二叉树,那么在类满二叉树下,叶节点最多,答案可能是1010;(不确定)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6+10;
int n = 2019;
int main(){
ll sum = 0;
int maxDeep = 0;
for(int depth = 0;depth<=10000;depth++){ //枚举满二叉树的层数
if(sum + pow(2,depth) > n) break;
sum += pow(2,depth);
maxDeep = depth;
}
cout<<(pow(2,maxDeep) - ((n-sum)/2)) + (n-sum); //最后一层有可能不满,那么倒数第二层有(pow(2,maxDeep) - ((n-sum)/2))个非叶子节点,再加上最后一层的叶子节点(n-sum)个
return 0;
}
4. 答案:544
在1至2019中,有多少个数的数位中包含数字9?
枚举1~2019,判断是否包含9
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6+10;
int cnt = 0;
bool contain(int x){
if(x == 9) return true;
if(x<9) return false;
while(x){
if(x%10 == 9) return true;
x = x/10;
}
return false;
}
int main(){
for(int i=1;i<=2019;i++){
if(contain(i)) cnt++;
}
cout<<cnt;
return 0;
}
5.
问题描述
在数列 a[1],a[2],...,a[n] 中,如果对于下标 i,j,k 满足 0<i<j<k<n+1 且 a[i]<a[j]<a[k],则称 a[i],a[j],a[k] 为一组递增三元组,a[j] 为递增三元组的中心。
给定一个数列,请问数列中有多少个元素可能是递增三元组的中心。
输入格式
输入的第一行包含一个整数 n。
第二行包含 n 个整数 a[1],a[2],...,a[n] ,相邻的整数间用空格分隔,表示给定的数列。
输出格式
输出一行包含一个整数,表示答案。
评测用例规模与约定
对于 50 的评测用例,2<=n<=100,0<=Num<=1000 。
对于所有评测用例,2<=n<=1000,0<=Num<=10000 。
50% 3层枚举,判递增
3层枚举,只要a[i] < a[j] < a[k]说明满足条件了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//50%
const int maxn = 1e5+100;
int a[maxn];
int n;
set<int> se;
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
ll cnt = 0;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
if(a[j] > a[i]){
for(int k=j+1;k<=n;k++){
if(a[k] > a[j])
se.insert(j);
}
}
}
}
cout<<se.size();
return 0;
}
100% 枚举中心点,O(n^2)
枚举中心点,查左边<i的,查右边>i的,如果中心点左边有比它小的数,同时中心点右边有比它大的数,就满足条件,总数+1。总时间复杂度O(n^2)。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//100% 枚举O(n^2)
const int maxn = 1e5+100;
int a[maxn];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
ll cnt = 0;
for(int center = 2;center<=n-1;center++){ //枚举中心点
int leftNum = 0,rightNum = 0;
for(int left = 1;left<center;left++){ //统计左边比它小的
if(a[left] < a[center]) leftNum++;
}
for(int right = center+1;right<=n;right++){ //统计右边比它大的
if(a[right] > a[center]) rightNum++;
}
if(leftNum * rightNum != 0) cnt++;
}
cout<<cnt;
return 0;
}
100% 树状数组优化O(nlongn)
树状数组维护分别正序和倒序维护各个数出现的次数,动态查询
1.正序建树:查询中心点左边比它的值小的个数,就是查此时1~i-1的数的个数
2.逆序建树:查询中心点右边比它的值大的个数,就是查此时i+1~n的数的个数
3.枚举中心点: 如果中心点左边有比它小的数,同时中心点右边有比它大的数,就是一个合法的中心点
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
/*
100% nlogn
树状数组维护分别正序和倒序维护各个数出现的次数,动态查询
1.正序建树:查询中心点左边比它的值小的个数,就是查此时1~i-1的数的个数
2.逆序建树:查询中心点右边比它的值大的个数,就是查此时i+1~n的数的个数
3.枚举中心点: 如果中心点左边有比它小的数,同时中心点右边有比它大的数,就是一个合法的中心点
*/
const int maxn = 1e5+100;
int C[maxn];
int a[maxn];
int n;
int cnt1[maxn],cnt2[maxn];
int lowbit(int x){
return x & -x;
}
int getsum(int x){ //查前缀和
int ans = 0;
while(x >= 1){
ans += C[x];
x = x - lowbit(x);
}
return ans;
}
void add(int x,int k){
while(x <= n){
C[x] = C[x] + k;
x = x + lowbit(x);
}
}
int query(int l,int r){ //区间查询
return getsum(r) - getsum(l-1);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) {
cin>>a[i];
add(a[i],1); //正序建树查左侧比i个元素小的
cnt1[i] = query(1,i-1);
}
memset(0,sizeof(C),0);
for(int i=n;i>=1;i--){ //倒序建树 查右侧比第i个元素大的
add(a[i],1);
cnt2[i] = query(i+1,n);
}
ll cnt = 0;
for(int i=1;i<=n;i++){ //枚举中心点
if(cnt1[i] && cnt2[i]) cnt++;
}
cout<<cnt;
return 0;
}
/*
5
1 2 5 3 5
*/
6.
问题描述
一个正整数如果任何一个数位不大于右边相邻的数位,则称为一个数位递增的数,例如 1135 是一个数位递增的数,而 1024 不是一个数位递增的数。
给定正整数 n ,请问在整数 1 至 n 中有多少个数位递增的数?
输入格式
输入的第一行包含一个整数 n 。
输出格式
输出一行包含一个整数,表示答案。
评测用例规模与约定
对于 40% 的评测用例,1<=n<=1000。
对于 80% 的评测用例,1<=n<=100000。
对于所有评测用例,1<=n<=1000000。
100%数据:枚举,倒着数字判递减,O(10^7)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//100%
const int maxn = 1e6+10;
int n;
bool solve(int x){
if(x < 10 ) return true;
int last = x%10;
x = x / 10;
while(x){
if(x%10 > last) return false;
last = x%10;
x = x / 10;
}
return true;
}
int main(){
cin>>n;
ll cnt = 0;
for(int i=1;i<=n;i++){
if(solve(i)) cnt++;
}
cout<<cnt;
return 0;
}
7.
问题描述
小明对类似于 hello 这种单词非常感兴趣,这种单词可以正好分为四段,第一段由一个或多个辅音字母组成,第二段由一个或多个元音字母组成,第三段由一个或多个辅音字母组成,第四段由一个或多个元音字母组成。
给定一个单词,请判断这个单词是否也是这种单词,如果是请输出yes,否则请输出no。
元音字母包括 a,e,i,o,u ,共五个,其他均为辅音字母。
输入格式
输入一行,包含一个单词,单词中只包含小写英文字母。
输出格式
输出答案,或者为 yes ,或者为 no 。
评测用例规模与约定
对于所有评测用例,单词中的字母个数不超过 100
100%数据 按题意字符串模拟
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6+10;
string a;
int main(){
cin>>a;
int pos = 1;
int level = 1;
bool flag = true;
int len = a.length();
while(pos < len){
if(level == 2){ //元音
int ago = pos;
while(pos < len && (a[pos] == 'a'|| a[pos] == 'e' || a[pos] == 'i' || a[pos] == 'o' || a[pos] == 'u')){
pos++;
}
if(pos == ago && !((a[pos] == 'a'|| a[pos] == 'e' || a[pos] == 'i' || a[pos] == 'o' || a[pos] == 'u'))) flag = false;
level++;
}else if(level == 1){
int ago = pos;
while(pos < len && (a[pos] != 'a'&& a[pos] != 'e' && a[pos] != 'i' && a[pos] != 'o' && a[pos] != 'u')){
pos++;
}
if(pos == ago && !(a[pos] != 'a'&& a[pos] != 'e' && a[pos] != 'i' && a[pos] != 'o' && a[pos] != 'u')) flag = false;
level++;
}else if(level == 4){ //元音
int ago = pos;
while(pos < len && (a[pos] == 'a'|| a[pos] == 'e' || a[pos] == 'i' || a[pos] == 'o' || a[pos] == 'u')){
pos++;
}
if(pos == ago && !((a[pos] == 'a'|| a[pos] == 'e' || a[pos] == 'i' || a[pos] == 'o' || a[pos] == 'u'))) flag = false;
level++;
}else if(level == 3){
int ago = pos;
while(pos < len && (a[pos] != 'a'&& a[pos] != 'e' && a[pos] != 'i' && a[pos] != 'o' && a[pos] != 'u')){
pos++;
}
if(pos == ago && !((a[pos] != 'a'&& a[pos] != 'e' && a[pos] != 'i' && a[pos] != 'o' && a[pos] != 'u'))) flag = false;
level++;
}else flag = false;
if(flag == false) break;
}
if(flag && level == 5) puts("yes");
else puts("no");
return 0;
}
8.
问题描述
小明有一块空地,他将这块空地划分为 n 行 m 列的小块,每行和每列的长度都为 1 。
小明选了其中的一些小块空地,种上了草,其他小块仍然保持是空地。
这些草长得很快,每个月,草都会向外长出一些,如果一个小块种了草,则它将向自己的上、下、左、右四小块空地扩展,这四小块空地都将变为有草的小块。
请告诉小明,k 个月后空地上哪些地方有草。
输入格式
输入的第一行包含两个整数 n , m 。
接下来 n 行,每行包含 m 个字母,表示初始的空地状态,字母之间没有空格。如果为小数点,表示为空地,如果字母为 g,表示种了草。
接下来包含一个整数 k。
输出格式
输出 n 行,每行包含 m 个字母,表示 k 个月后空地的状态。如果为小数点,表示为空地,如果字母为 g,表示长了草。
评测用例规模与约定
对于 30% 的评测用例,2<=n,m<=20。
对于 70% 的评测用例,2<=n,m<=100。
对于所有评测用例,2<=n,m<=1000,1<=k<=1000。
70% 模拟
按题意模拟,开一个新数组更新草地,更新完将复制给旧数组。一月更新一次。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1100;
int n,m,k;
char a[maxn][maxn];
char s[maxn][maxn];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) {
cin>>a[i][j];
s[i][j] = a[i][j];
}
}
cin>>k;
for(int i=1;i<=k;i++){
for(int p = 1;p <= n;p++){
for(int q = 1;q <= m;q++){
if(a[p][q] == 'g'){
s[p-1][q] = 'g';
s[p+1][q] = 'g';
s[p][q-1] = 'g';
s[p][q+1] = 'g';
}
}
}
for(int p=1;p<=n;p++){
for(int q=1;q<=m;q++) a[p][q] = s[p][q];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout<<a[i][j];
}
cout<<endl;
}
return 0;
}
/*
2 2
.g
..
1
*/
100% bfs搜索
把最初是'g'的坐标先入队列,跑bfs,bfs分层的性质保证了 土地每次都是向外一次一次扩展(即:每个月用最外层的草地扩展一次),每次扩展把4个方向满足条件的加入队列。直到dist=k 说明从最初的g点已经走了k个距离 不能再走下去了。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1100;
int n,m,k;
char a[maxn][maxn];
struct node{
int x,y,dist;
};
queue<node> que;
void bfs(){
while(!que.empty()){
node u = que.front(); //取出队头
que.pop();
if(u.dist == k) continue; //dist=k 说明从最初的g点已经走了k个距离 不能再走下去了
int x = u.x,y = u.y,dist = u.dist;
//把4个方向满足条件的加入队列 作一次扩展
if(x+1<=n && a[x+1][y] != 'g'){
a[x+1][y] = 'g';
que.push({x+1,y,dist+1});
}
if(y+1<=m && a[x][y+1] != 'g'){
a[x][y+1] = 'g';
que.push({x,y+1,dist+1});
}
if(x-1>=1 && a[x-1][y] != 'g'){
a[x-1][y] = 'g';
que.push({x-1,y,dist+1});
}
if(y-1>=1 && a[x][y-1] != 'g'){
a[x][y-1] = 'g';
que.push({x,y-1,dist+1});
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) {
cin>>a[i][j];
if(a[i][j] == 'g') que.push({i,j,0}); //把最初是'g'的先入队
}
}
cin>>k;
bfs();//跑一遍bfs bfs分层的性质保证了 土地每次都是向外一次一次扩展(即:每个月用最外层的草地扩展一次)
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) {
cout<<a[i][j];
}
cout<<endl;
}
return 0;
}
/*
4 5
.g...
.....
..g..
.....
2
*/
100% 二维差分
每一个初始点g,影响的范围是一个菱形,用二维差分标记
参考这道题:https://www.cnblogs.com/fisherss/p/10388172.html
9.
问题描述
小明想知道,满足以下条件的正整数序列的数量:
第一项为 n ;
第二项不超过 n ;
从第三项开始,每一项小于前两项的差的绝对值。
请计算,对于给定的 n ,有多少种满足条件的序列。
输入格式
输入一行包含一个整数 n 。
输出格式
输出一个整数,表示答案。答案可能很大,请输出答案除以 10000 的余数。
评测用例规模与约定
对于 20% 的评测用例,1<=n<=5。
对于 50% 的评测用例,1<=n<=10。
对于 80% 的评测用例,1<=n<=100。
对于所有评测用例,1<=n<=1000。
50% dfs暴力搜索
n==2的时候 有n种方案,分别可以放1~n;
dfs判n>3的情况
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//50% dfs暴力搜索
const int maxn = 1010;
int n;
ll cnt = 0;
int a[maxn];
void dfs(int pos,int u,int v){ //判n>3的情况
cnt = (cnt+1)%10000;
int d = abs(v-u);
if(d == 0) return;
for(int i=1;i<d;i++){
a[pos] = i;
dfs(pos+1,i,u);
}
}
int main(){
cin>>n;
a[1] = n;
for(int i=n;i>=1;i--){ //n==2的时候 有n种方案,分别可以放1~n
a[2] = i;
dfs(3,i,n);
}
cout<<cnt;
return 0;
}
80%数据 记忆化搜索
开个map作缓存,能过80%数据
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//80% 记忆化搜索
int n;
map<pair<int,int>,int > mp;
int dfs(int u,int v){
if(mp[make_pair(u,v)]) return mp[make_pair(u,v)];
int d = abs(v-u);
if(d == 0) return mp[make_pair(u,v)] = 1;
ll cnt = 1;
for(int i=1;i<d;i++){
cnt = (cnt + dfs(i,u))%10000;
}
return mp[make_pair(u,v)] = cnt%10000;
}
int main(){
cin>>n;
ll ans = 0;
for(int i=n;i>=1;i--){
ans = (ans + dfs(i,n))%10000;
}
cout<<ans;
return 0;
}
##100%数据 记忆化搜索 + 打表法 在记忆化搜索的基础上,打表 本地打表的测试代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//100% 打表法: 本地打表的测试代码
int n;
map<pair<int,int>,int > mp;
int dfs(int u,int v){
if(mp[make_pair(u,v)]) return mp[make_pair(u,v)];
int d = abs(v-u);
if(d == 0) return mp[make_pair(u,v)] = 1;
ll cnt = 1;
for(int i=1;i<d;i++){
cnt = (cnt + dfs(i,u))%10000;
}
return mp[make_pair(u,v)] = cnt%10000;
}
int main(){
freopen("9.txt","w",stdout);
printf("int table[1100] = {0,");
for(n = 1;n<=1000;n++){
ll ans = 0;
for(int i=n;i>=1;i--){
ans = (ans + dfs(i,n))%10000;
}
printf("%d",ans%10000);
if(n!=1000) printf(",");
}
printf("}");
return 0;
}
打表后正式上交的代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
//100% 打表上交的代码
int n;
int table[1100] = {0,1,2,4,7,14,26,53,106,220,452,946,1967,4128,8638,8144,8068,........篇幅有限见下图};
int main(){
cin>>n;
cout<<table[n];
return 0;
}

10.
问题描述
小明要组织一台晚会,总共准备了 n 个节目。然后晚会的时间有限,他只能最终选择其中的 m 个节目。
这 n 个节目是按照小明设想的顺序给定的,顺序不能改变。
小明发现,观众对于晚上的喜欢程度与前几个节目的好看程度有非常大的关系,他希望选出的第一个节目尽可能好看,在此前提下希望第二个节目尽可能好看,依次类推。
小明给每个节目定义了一个好看值,请你帮助小明选择出 m 个节目,满足他的要求。
输入格式
输入的第一行包含两个整数 n , m ,表示节目的数量和要选择的数量。
第二行包含 n 个整数,依次为每个节目的好看值。
输出格式
输出一行包含 m 个整数,为选出的节目的好看值。
评测用例规模与约定
对于 30% 的评测用例,1<=n<=20;
对于 60% 的评测用例,1<=n<=100;
对于所有评测用例,1<=n<=100000,0<=value<=100000。
60% 枚举
按题意模拟
1.每次选1个数 i∈1~m
2.当前这个数就是: 上一次选的数的右边 ~ n-(m-i)的区间内的最大值,这里可以O(n)枚举,也可以O(longn)优化
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
/*
60%
1.每次选1个数 i∈1~m
2.当前这个数就是: 上一次选的数的右边 ~ n-(m-i)的区间内的最大值,这里可以O(n)枚举,也可以O(longn)优化
*/
const int maxn = 1e5+100;
int n,m;
int a[maxn];
int b[maxn];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
int pos = 0;
for(int i = 1;i<=m;i++){ //选第i个数
int maxi = a[pos+1];
for(int j=pos+1;j<n-(m-i)+1;j++){ //pos+1 ~ n-(m-i)+1可以选择
if(a[j] > maxi){ //选出这个区间内最大的,并更新最大值和所在位置下标
maxi = a[j];
pos = j;
}
}
b[i] = maxi;
}
for(int i=1;i<m;i++) cout<<b[i]<<" ";
cout<<b[m];
return 0;
}
100% 线段树优化查询
按60%的思路中的查询可以用线段树优化,用线段树查询区间最大值,并记录结点的位置下标 ,时间复杂度O(nlongn)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
/*
100% 开一个线段树维护区间最大值 并记录结点的位置下标
1.每次选1个数 i∈1~m
2.当前这个数就是: 上一次选的数的右边 ~ n-(m-i)的区间内的最大值,可以O(longn)优化
*/
const int maxn = 1e5+100;
int n,m;
int a[maxn];
int b[maxn];
struct node{
int pos;
ll maxv;
}tree[maxn*4];
void pushup(int o){
if(tree[o<<1].maxv > tree[o<<1|1].maxv){
tree[o].maxv = tree[o<<1].maxv;
tree[o].pos = tree[o<<1].pos;
}else{
tree[o].maxv = tree[o<<1|1].maxv;
tree[o].pos = tree[o<<1|1].pos;
}
}
void build(int o,int l,int r){
//初始化结点的标记
tree[o].maxv = 0;
//叶子结点
if(l == r){
tree[o].pos = l;
tree[o].maxv = a[l];
return;
}
int mid = (l+r)>>1;
build(o<<1,l,mid);
build(o<<1|1,mid+1,r);
pushup(o);
}
void update(int o,int l,int r,int pos,int v){
if(l == r){ //完全包含该l~r区间
tree[o].maxv += v;
return;
}
int mid = (l+r)>>1;
if(pos <= mid) update(o<<1,l,mid,pos,v);
else update(o<<1|1,mid+1,r,pos,v);
pushup(o);
}
pair<int,ll> querymax(int o,int l,int r,int ql,int qr){
if(ql <= l && r <= qr){ //完全包含 直接return
return make_pair(tree[o].pos,tree[o].maxv);
}
int mid = (l+r)>>1;
//查询出区间最大的max
pair<int,ll> temp,u,v;
if(ql<=mid) {
u = querymax(o<<1,l,mid,ql,qr);
temp = u;
}
if(qr>mid) {
v = querymax(o<<1|1,mid+1,r,ql,qr);
if(v.second > temp.second) temp = v;
}
return temp;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
int pos = 0;
for(int i = 1;i<=m;i++){ //选第i个数
int maxi = a[pos+1];
//查询pos+1~(n-(m-i) 闭区间的最大值
pair<int,ll> u = querymax(1,1,n,pos+1,n-(m-i));
pos = u.first; //第i个数选了pos位置
maxi = u.second; //第i个数选了maxi这个值
b[i] = maxi;
}
for(int i=1;i<m;i++) cout<<b[i]<<" ";
cout<<b[m];
return 0;
}
/*
5 3
3 1 2 5 4
*/
不保证每个点的正确性...思路仅供参考...


