牛客寒假6-C |二分优化dp，LIS

思路

最长不上升子序列
dp[i] 表示以第i个元素结尾的最长不上升子序列
转移方程 dp[i] = max(dp[i],dp[j] + 1:if(h[j] > h[i]) j∈1~i-1
优化思路：dp的值相同时,保留较大的数(这里指y的指)显然更好,以尽可能使得前面的数大
所有引出d数组单调下降 可用来二分

下图补充LIS引进二分优化的例子：转载计蒜客

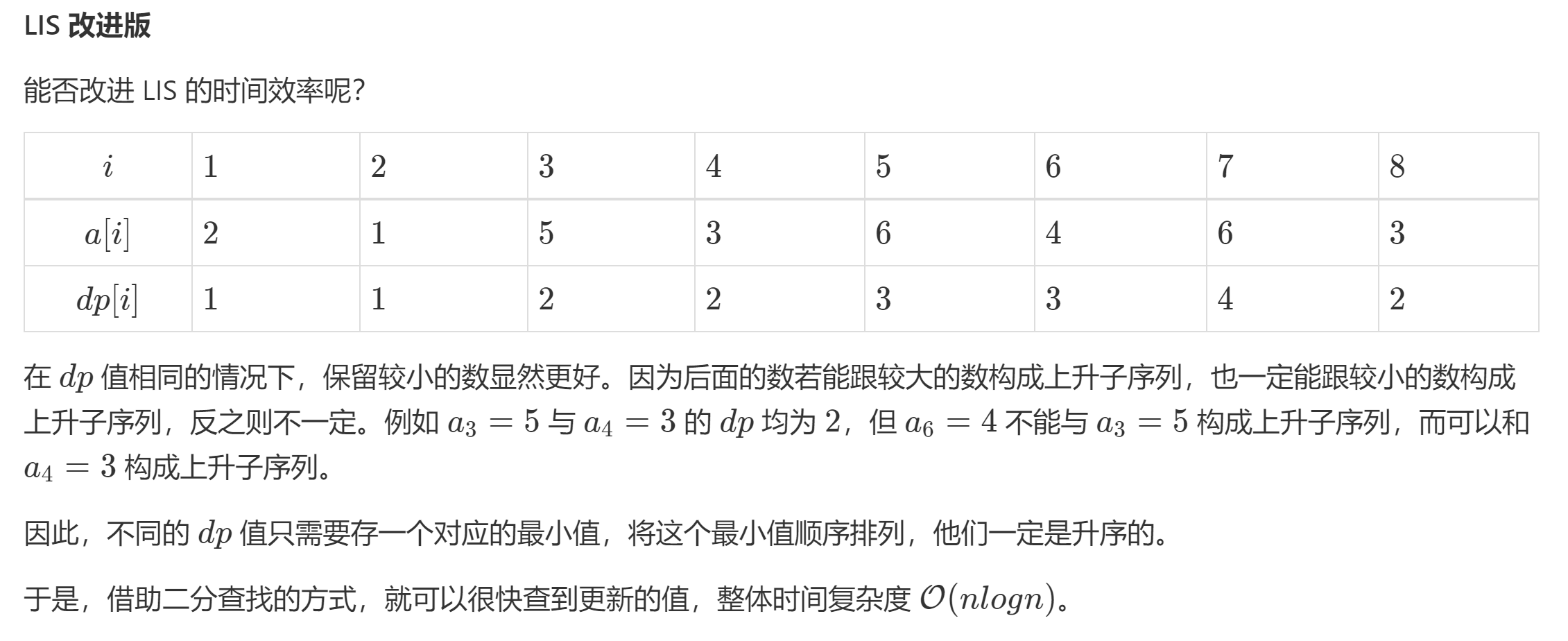
代码

#include<bits/stdc++.h>
using namespace std;

const int maxn = 100010;
int n;

struct node{
	int x,y;
	int pos;
}a[maxn];
int len = 0;
int d[maxn];
int b[maxn];

bool cmp(node u,node v){
	if(u.x == v.x) return u.y < v.y;
	return u.x < v.x;
}

int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i].x>>a[i].y;
		a[i].pos = i;
	} 
	sort(a+1,a+n+1,cmp);
	d[++len] = a[1].y;
	b[a[1].pos] = 1;
	for(int i=2;i<=n;i++){
		if(a[i].y < d[len]) d[++len] = a[i].y,b[a[i].pos] = len;
		else{
			//找第一个小于的 
			int pos = upper_bound(d+1,d+len+1,a[i].y,greater<int>()) - d;
			d[pos] = a[i].y;
			b[a[i].pos] = pos;
		}
	}
	cout<<len<<endl;
	for(int i=1;i<=n;i++) cout<<b[i]<<" ";
	return 0;
}