牛客寒假5-F碎碎念| dp + 前缀和

题目地址：https://ac.nowcoder.com/acm/contest/3006/F

思路

1.区间查询，想到前缀和，所以主要就是计算喊i声时的方案数

2-1思路1：考虑递推关系
一维递推关系
假设前i-1声已经算过，那么第i声时方案数怎么计算？
容易想到👇
第i声方案数 = 第i-1声AC方案数(这一次ac) + 第i-x声方案数(这一次wa，i-x~x内算在这一次wa时的贡献里)
dp[i] = dp[i-1] + dp[i-x-1]

3.初始化边界
dp[i] = 1;
dp[x] = 2;

思路2：二维递推

初始化边界：dp[i][0] = 1;第i声是AC的方案数 = 1；

4.计算前缀和，区间查询 sum(r) - sum(l-1)即为[l,r]的方案数

AC代码

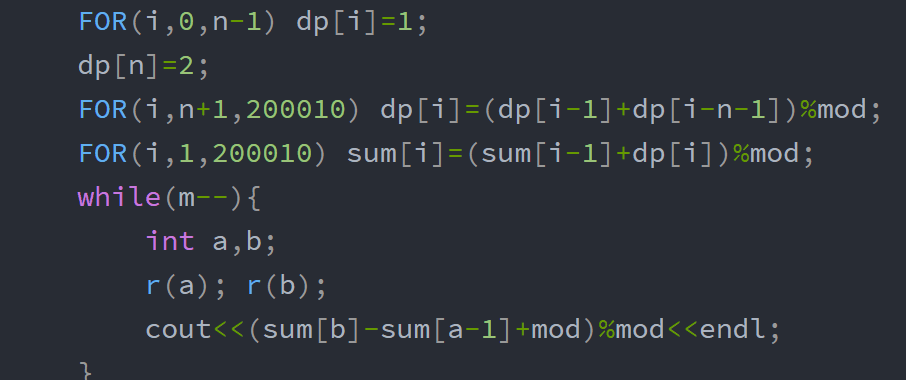
思路1

转载

思路2

#include <bits/stdc++.h>
#define maxn 200005
typedef long long ll;
const ll mod = 1e9 + 7;
using namespace std;
int N, M, K;
ll dp[maxn][2];	
ll f[maxn];
int main(){
	int x;
	cin >> x;dp[x][1] = 1;
	for (int i = 1; i <= x; i++)
		dp[i][0] = 1;
	for (int i = x + 1; i <= 100000; i++) {
		dp[i][0] = (dp[i - 1][0] + dp[i - 1][1])%mod; //ac
		dp[i][1] = (dp[i][1] + dp[i - x][0])%mod; //wa
	}
	for (int i = 1; i <= 100000; i++)
		f[i] = (dp[i][0] + dp[i][1] + f[i - 1]) % mod; //前缀和 
	int t;
	cin>>t;
	while (t--) {
		int l, r;
		cin>>l>>r;
		cout<<(f[r] - f[l - 1] + mod) % mod <<endl;
	}
	return 0;
}