牛客寒假6-B图| 统计环中结点个数，计算最大链长

思路

每个点出度都为1的有向图是一个基环内向树森林。
要用到的结论是：从一个点出发，沿着出边一路走下去，一定会走到一个环。

思路-两个步骤:
遍历起点，dfs时存储以这个点为起点的路径长度，遇到环要把环上所有点的值赋值成相同值
1.统计环个数, 把各个结点值赋值为所在环的结点数量
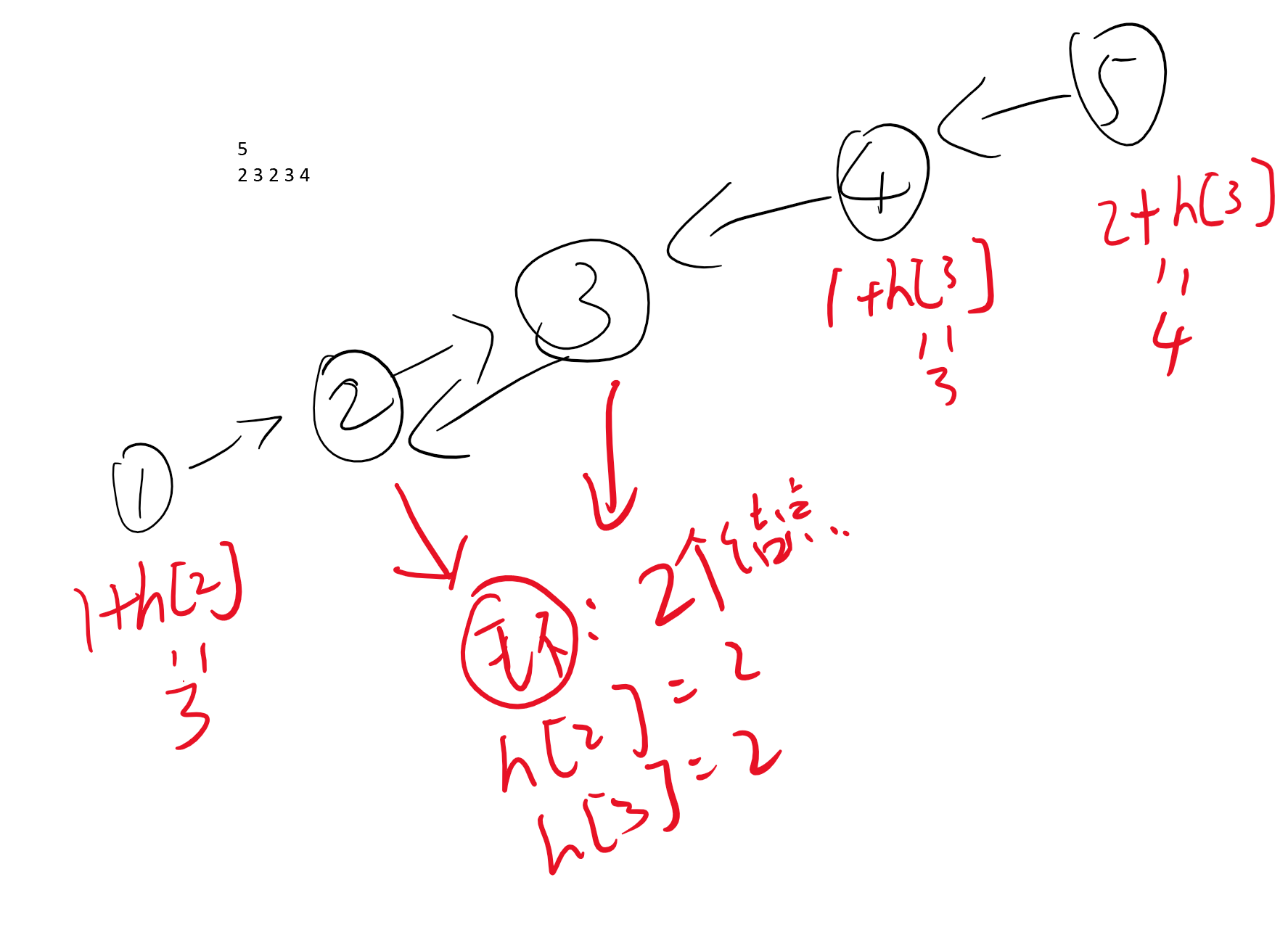
2.统计各个点到环的距离,更新最大值，最大链长就是环里的结点个数 + 起点点到环的距离

题目地址：https://ac.nowcoder.com/acm/contest/3007/B
参考题解：https://blog.csdn.net/weixin_45766122/article/details/104332347

看图理解更清晰。

AC代码

#include<bits/stdc++.h>
#define ll long long
#define maxn 1000005
using namespace std;

int n,ans,h[maxn],child[maxn];
int vis[maxn];

//基环内向树森林: 从一个点出发，沿着出边一路走下去，一定会走到一个环。 

/*
两个步骤:
	1.统计环个数, 把各个结点值赋值为所在环的结点数量 
	2.统计各个点到环的距离,更新最大值
*/ 
void dfs(int id){
	//1. 暴力统计环 h[child] = 0 说明从有人到达了'我'儿子, 我也能到达我儿子,说明有环了 
    //注: h[child[id] = 0 是一个重要的特征 这时环的起点找到了 就是id->child[id]这条边形成了环 
	if(h[child[id]]==0){ 
        int res = 1;
        int k = child[id];
        while(k != id){ //遇到环 记录环中结点个数 
            res++;
            k=child[k];
        }
        h[k]=res;
        vis[k]=1;
        k=child[k];
        while(k!=id){ //把环上所有点赋值为环中结点的个数  作为他们共同的高度 
            h[k]=res;
            vis[k]=1;
            k=child[k];
        }
        return ;
    }
    
    //2. 下面就是 统计当前点到环的距离 再加上环中结点个数(已经算成结点个数作为距离存储到h数组中了) 
    h[id]=0; //高度设置成0 
    if(vis[child[id]]==0){ //孩子没有去过 
        dfs(child[id]); //去孩子那里玩玩 
        //vis[id] = 0 说明 dfs孩子的过程没有标记我id, 说明我不在儿子形成的环里
        if(vis[id]==0){
            h[id]=h[child[id]]+1; //按正常的dp思想+1距离就行  
            vis[id]=1;
        }
        //else 我和child共同在环中 权值h已经统计成环中结点的数量了 
    }
    else if(vis[child[id]]=1){ //要是孩子被别人去过了 
        h[id]=h[child[id]]+1; //孩子肯定是有值的 赋值为 "孩子到别人的距离再+1"的距离,这里的1是指我到孩子的距离, 
        vis[id] = 1; //标记访问过 
		return ;
    }
    
    return;
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&child[i]); //输入孩子 存储图 
    }
    for(int i=1;i<=n;i++) h[i]=-1; //初始化高度 
    ans=0;
    for(int i=1;i<=n;i++){ //遍历起点 
        if(vis[i]==0) dfs(i); //dfs没有标记的点 
        ans=max(ans,h[i]);
    }
    printf("%d",ans);
    return 0;
}
/*
5
2 3 2 3 4
*/