写完代码就去吃饺子|The 10th Henan Polytechnic University Programming Contest

河南理工大学第十届校赛

很久没有组队打比赛了，好吧应该说很久没有写题了，
三个人一起玩果然比一个人玩有趣多了。。。
前100分钟过了4题，中途挂机100分钟也不知道什么原因，可能是因为到饭点太饿了？，最后100分钟一人开一题差点冲到榜首也太刺激了吧！
是一次愉快的游戏体验。
下周去农大参加邀请赛，希望能和今天一样快乐~

今天是冬至，别忘记吃饺子！

题解和代码

A. Dong Zhi

A题地址
题意：输出"Let's eat dumplings"，这句话
思路：看标题肯定签到了，但是hpu前5分钟好卡，网速拼不过。

#include<bits/stdc++.h>
using namespace std;

int main(){
	cout<<"Let's eat dumplings"<<endl;
	return 0;
}

##B. The flower [B题地址](https://hpuoj.com/contest/32/problem/B/) 题意：统计字符串中出现次数>2的，长度为T的子串。从小到大按字典序输出子串。思路：用unorder_map统计子串出现的次数。substr(i,k)截取字符串。 ``` #include #include using namespace std;

string s;
string flower = "flower";
int k;
unordered_map<string,int >mp;
vector ans;

int main(){
cin>>s>>k;
int len = s.length();
string temp;
for(int i=0;i+k<=len;i++){
temp = s.substr(i,k);
mp[temp]++;
}
unordered_map<string,int >:: iterator it = mp.begin();
while(it != mp.end()){
if(it->second > 2) ans.push_back(it->first);
it++;
}
sort(ans.begin(),ans.end());
printf("%d\n",ans.size());
for(int i=0;i<ans.size();i++) printf("%s\n",ans[i].c_str());
return 0;
}

<br/>

## C. Xor Path
[C题地址](https://hpuoj.com/contest/32/problem/C/)
题意：一颗树，Q次查询，求两个结点最小的异或和。
思路：求最近公共祖先，dfs求每个结点到根节点1的路径异或和，lca优化，复杂度qlogn

include<bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 1e6+100;
vector g[maxn];
int pre[maxn],a[maxn],parent[maxn],f[maxn][30],depth[maxn];
ll bit[30];

//初始化bit数组:求2的i次幂
void init(){
bit[0] = 1;
for(int i=1;i<=29;i++){
bit[i] = (bit[i-1]<<1);
}
}

void dfs(int u,int par){
depth[u] = depth[par] + 1;
f[u][0] = par;
for(int i=1;bit[i]<=depth[u];i++) f[u][i] = f[f[u][i-1]][i-1];
for(int v:g[u]){
if(v!=par) dfs(v,u);
}
}

//求x和y的最近公共祖先
int lca(int x,int y){
if(depth[x] < depth[y]) swap(x,y);
for(int i=29;i>=0;i--){
if(depth[x] - depth[y] >= bit[i]) x = f[x][i];
}
if(x == y) return x;
for(int i=29;i>=0;i--){
if(depth[x] >= (1<<i) && f[x][i] != f[y][i]){
x = f[x][i];
y = f[y][i];
}
}
return f[x][0];
}

void DFS1(int u,int fa){
parent[u] = fa;
pre[u] = pre[fa]^a[u];
for(int v:g[u]){
if(v == fa) continue;
DFS1(v,u);
}
}

int main(){
int n,u,v,q;
//输入数据
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
init();
//建图邻接表
for(int i=0;i<=n;i++) g[i].clear();
for(int i=1;i<=n-1;i++){
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,0);
//dfs计算从根节点到每个结点的异或和
DFS1(1,0);
int x,y;
cin>>q;
while(q--){
cin>>x>>y;
int c = lca(x,y); //求x,y的最近公共祖先
int f = parent[c]; //求最近公共祖先的父节点这里再求一次父节点的原因是: 消除祖先的父节点到根节点这段路径(异或了2次)的异或
cout<<(pre[x]^pre[y]pre[f]^pre[c])<<endl; //画图理解树链上异或两次就等于没有异或消除祖先的父节点到根节点这段路径(异或了2次)的异或
}
return 0;
}


## D. LaunchPad
[D题地址](https://hpuoj.com/contest/32/problem/D/)
题意：翻转pad，每次翻转第x一整行和第y一整列，求Q次后最终翻转为亮面的个数
思路：队友过的。。似乎开两个一维数组，一个统计行，一个统计列，判断奇偶就可以了

include

using namespace std;
int mp[1005][1005];
int main(){
int m,n;cin>>n>>m;
int q;cin>>q;
int visX[1005];
int visY[1005];
memset(visX,0,sizeof(visX));
memset(visY,0,sizeof(visY));
while(q--){
int x,y;
cin>>x>>y;
visX[x]++;
visY[y]++;
mp[x][y]++;
}
int ans = 0;
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
if((visX[i]+visY[j]+mp[i][j])%2!=0){
ans++;
}
}
}
cout<<ans;
return 0;
}

<br/>

## E. Morse code
[E题地址](https://hpuoj.com/contest/32/problem/E/)
题意：给一个字符串，找最长可以匹配莫斯码成功的字母长度。
思路：这。。队友过的，我题目还没看完，他就过了。等等？？看了看他代码，也太秀了。

include

include<string.h>

include

using namespace std;

typedef long long ll;
const int maxn =2e5+10;
const ll N=1e9+7;

bool flag;
int main()
{
int t;
cin >> t;
while(t--)
{
string s;
cin >> s;
ll ans=s.size()/2; //这样就行了嘛??
cout << ans << endl;
}
return 0;
}

<br/>
## F. For language
[F题地址](https://hpuoj.com/contest/32/problem/F/)
题意：计算时间复杂度。
思路：一行一行读，看第一个输入的字符串是什么就，按什么来

include<bits/stdc++.h>

using namespace std;

typedef long long ll;
const ll mod = 1e9+7;
int n;

ll get(string x,string y){
ll xx = 0;
for(int i=0;i<x.length();i++){
xx = xx10 + (x[i] - '0');
}
ll yy = 0;
for(int i=0;i<y.length();i++){
yy = yy10 + (y[i] - '0');
}
return (yy - xx + 1) % mod;
}

int main(){
cin>>n;
bool develop = 0;
ll ans = 0;
ll value = 0;
for(int line=1;line<=n;line++){
string first;
cin>>first;
if(first == "begin"){
develop = 1;
value = -1;
}else if(first == "for" && develop==1){
string a;
cin>>a;
string num1;
cin>>num1;
string num2;
cin>>num2;
ll cur = get(num1,num2)%mod;
//判断等于0的情况
if(value == -1) value = 1;
value = (value * cur) % mod;
}else if(first == "end"){
develop = 0;
if(value != -1)
ans = (ans + value)%mod;
}
}
cout<<ans;
return 0;
}

<br/>

## G. Puzzle
[G题地址](https://hpuoj.com/contest/32/problem/G/)
题意：累加一个数每一位上的cycle值，其中1, 2, 3, 5, 7 have 0 cycle, 4, 6, 9 have 1 cycle and 8 has 2 cycles.
思路：看懂样例，就可以直接做了

include<bits/stdc++.h>

using namespace std;

typedef long long ll;
int t;

int a[10] = {1,0,0,0,1,0,1,0,2,1};

int main(){
cin>>t;
while(t--){
ll x;
cin>>x;
ll temp = x;
int ans = 0;
while(temp){
ans+=a[temp%10];
temp/=10;
}
cout<<ans<<endl;
}
return 0;
}

<br/>
## H. Triangle tower
[H题地址](https://hpuoj.com/contest/32/problem/H/)
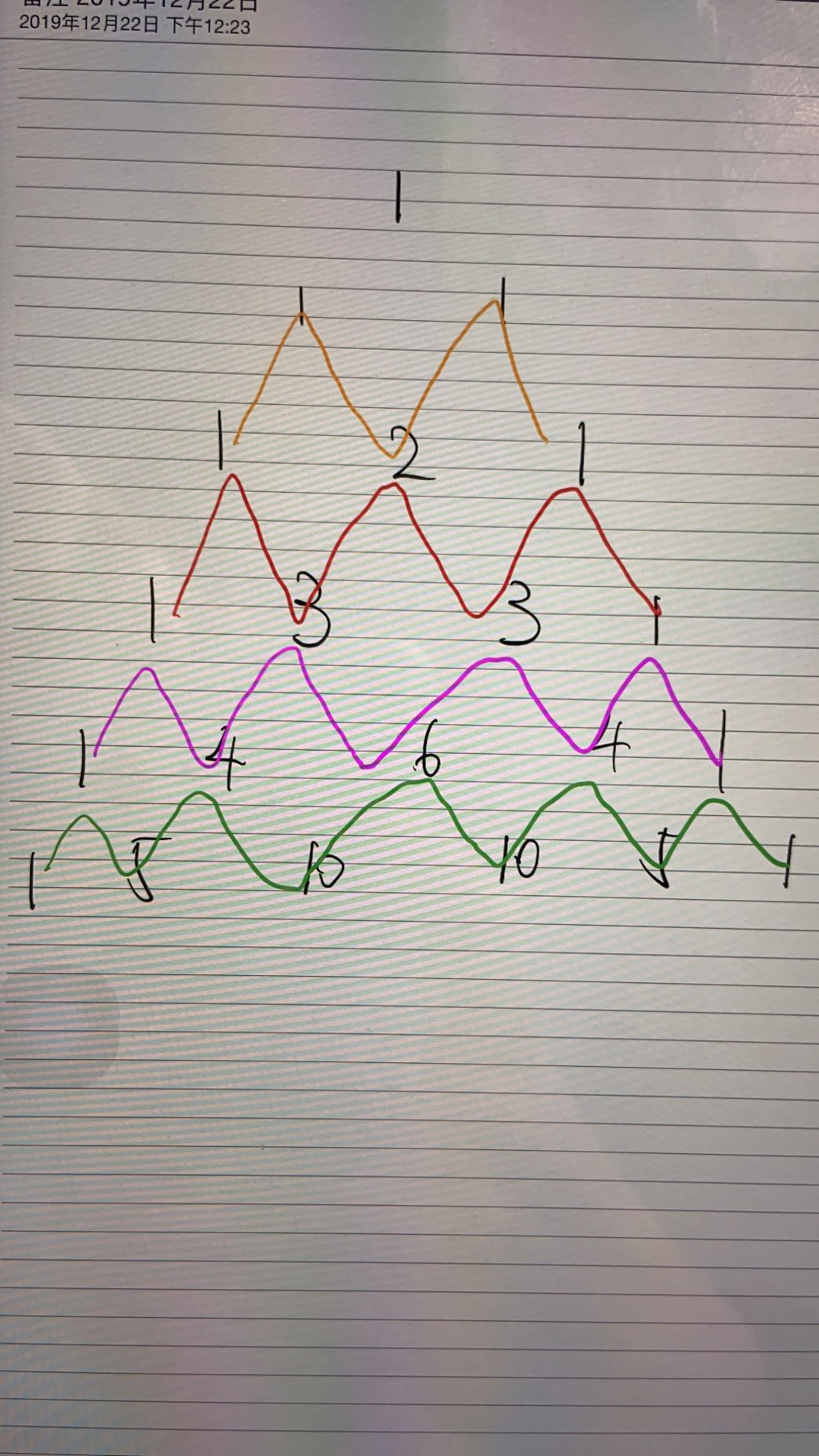
不是动态规划，队友过的，组合数，和杨辉三角有关。
放上队友在地铁上画的两张图。。。
![](https://img2018.cnblogs.com/blog/1454456/201912/1454456-20191222164640056-1834506144.png)
![](https://img2018.cnblogs.com/blog/1454456/201912/1454456-20191222164719199-1709997521.png)

include

using namespace std;
const int mod = 1e9+7;
const int maxn = 1e5+5;
typedef long long ll;
ll c[maxn];//组合数 1 1e5
ll fac[maxn];
ll inv[maxn];
ll qpow(long long a,long long b)
{
ll ans=1;
ll k=a;
while(b)
{
if(b&1)ans=ansk%mod;
k=kk%mod;
b>>=1;
}
return (ans+mod)%mod;
}
void init(){
long long i;
fac[0]=1;
inv[0]=1;
fac[1]=1;
inv[1]=1;
for (i=2;i<maxn;i++){
fac[i]=((fac[i-1]i)%mod+mod)%mod;
inv[i]=(qpow(fac[i],mod-2)+mod)%mod;
}
}
ll C(ll n,ll m){
if (n<m||m<0) return 0;
return (fac[n]inv[m]%modinv[n-m]%mod+mod)%mod;
}
int main(){
int t;
cin>>t;
init();
while(t--){
int m,n;
cin>>n>>m;
ll ans;
if(m%2 == 1){
m = m/2+1;
m--;
n--;
int t = n - m;
ans = C(n,m);
}
else{
m = m/2;
m--,n-=2;
int t = n - m;
//cout<<c[n]<<" "<<c[m]<<" "<<c[t];
ll t1 = (c[m]c[t])%mod;
ans = C(n,m);
}//用上一行
cout<<ans<<endl;
}
return 0;
}

<br/>
## I. Kingdom of Mathematics
[I题地址](https://hpuoj.com/contest/32/problem/I/)
没做，还不会。
<br/>
##J. HPU's birthday
[J题地址](https://hpuoj.com/contest/32/problem/J/)
题意：给一个数n，求这个数n的二进制字符串，再把这个二进制字符串循环拼接n次，求最终i,j,k能组成110的组数
思路：我做了半天，思路错了；队友想到可以遍历最终拼接后的字符串，每次出现0，就统计前面有多少个1，选出两个1就可以了。比如前面出现了x个1，就计算C(x,2)
所以最后用了 前缀和，AC了,但是不要忘了开longlong，乘法会溢出！！wa了7次就这个原因。。怪自己很久没写代码细节都忘了。

include<bits/stdc++.h>

using namespace std;

typedef long long ll;
const ll mod = 1e9+7;
//const ll maxn = 2e6+10;
const int maxn = 1700000;
ll C[maxn];
int t;
ll n;
vector vec;
vector v;
vector ans;

void cov(ll x){
vec.clear();
v.clear();
if(x == 0) {
v.push_back(0);
return;
}
while(x){
vec.push_back(x%2);
x = x/2;
}
for(int i=vec.size()-1;i>=0;i--) v.push_back(vec[i]);
}

void init(){
for(ll i=1;i<=maxn;i++){
C[i] = ((i*(i-1))/2)%mod;
}
}

ll a[maxn];

int main(){
init();
cin>>t;
while(t--){
cin>>n;
cov(n);
ans.clear();
ans.push_back(0);
for(ll i=1;i<=n;i++){
for(int j=0;j<v.size();j++) ans.push_back(v[j]);
}
a[0] = 0;
for(int i=1;i<ans.size();i++){
if(ans[i] == 1) a[i] = a[i-1]+1;
else a[i] = a[i-1];
}
int len = ans.size();
ll answer = 0;
for(int i=1;i<len;i++){
if(ans[i] == 0){
answer = (answer + C[a[i]])%mod;
}
}
cout<<answer%mod<<endl;
}
return 0;
}

<br/>

## K. Max Sum
[K题地址](https://hpuoj.com/contest/32/problem/K/)
思路：两颗线段树:tp维护最小前缀和,tn维护最小后缀和
要计算[L,R]上的最大区间和,(其中 L<=i,R<=i+ki,L<=R)
只需要求出区间[i-ki-1,i-1]的最小前缀和 和 区间[i+1,i+ki+1]的最小后缀和
数组总和减去这两部分的值就是第i个位置上的最大wonderful interval

include<bits/stdc++.h>

using namespace std;

define ll long long

const int maxn=1000000+10;
const int INF=0x3f3f3f3f;
int a[maxn];
ll pre[maxn],nxt[maxn];
int k[maxn];
int N;

//线段树单点更新区间求和
struct Tree{
ll x[maxn];
//初始化
void init(int x){
N=1;
while(N<=x2) N=2;
}
//单点更新
void update(int k,int q){
k+=N-1;
x[k]=q;
while(k){
k=(k-1)/2;
x[k]=min(x[k2+1],x[k2+2]);
}
}
//区间查询
ll query(int a,int b,int l,int r,int k){
if(r<a || b<l) return INF; //处理边界
if(a<=l && r<=b) return x[k]; //处理边界
else{
ll vl=query(a,b,l,(l+r)/2,k2+1);
ll vr=query(a,b,(l+r)/2+1,r,k2+2);
return min(vl,vr);
}
}
}tp,tn;

int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&k[i]);
tp.init(n);
//前缀和建线段树
ll sum=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
sum+=a[i];
tp.update(i,sum);
}
//后缀和建线段树
sum=0;
for(int i=n;i>=1;i--){
sum+=a[i];
tn.update(i,sum);
}
//i从1~n sum为数组总和定义的最大区间值就=sum-最小前缀-最小后缀
ll ans=0;
for(int i=1;i<=n;i++){
ans+=sum;
ans-=tp.query(max(i-k[i]-1,0),max(i-1,0),0,N-1,0);
ans-=tn.query(min(i+1,n+1),min(i+k[i]+1,n+1),0,N-1,0);
}
printf("%lld\n",ans);
return 0;
}


## L. Restore Expressions
思路：两个始自终除第一个数a，b外其它全取1，另表达式右端=0，计算使a，b恢复到正数的最大次数。

posted @ 2019-12-22 16:57 fishers 阅读(299) 评论(0) 编辑收藏举报

刷新页面返回顶部

FISHers

写完代码就去吃饺子|The 10th Henan Polytechnic University Programming Contest

河南理工大学第十届校赛

题解和代码

A. Dong Zhi

include<bits/stdc++.h>

include

include

include

include

include

include

include

include

include

include

include

include<string.h>

include

include

include<bits/stdc++.h>

include<bits/stdc++.h>

include

include

include

include

include

include<bits/stdc++.h>

include<bits/stdc++.h>

define ll long long

公告