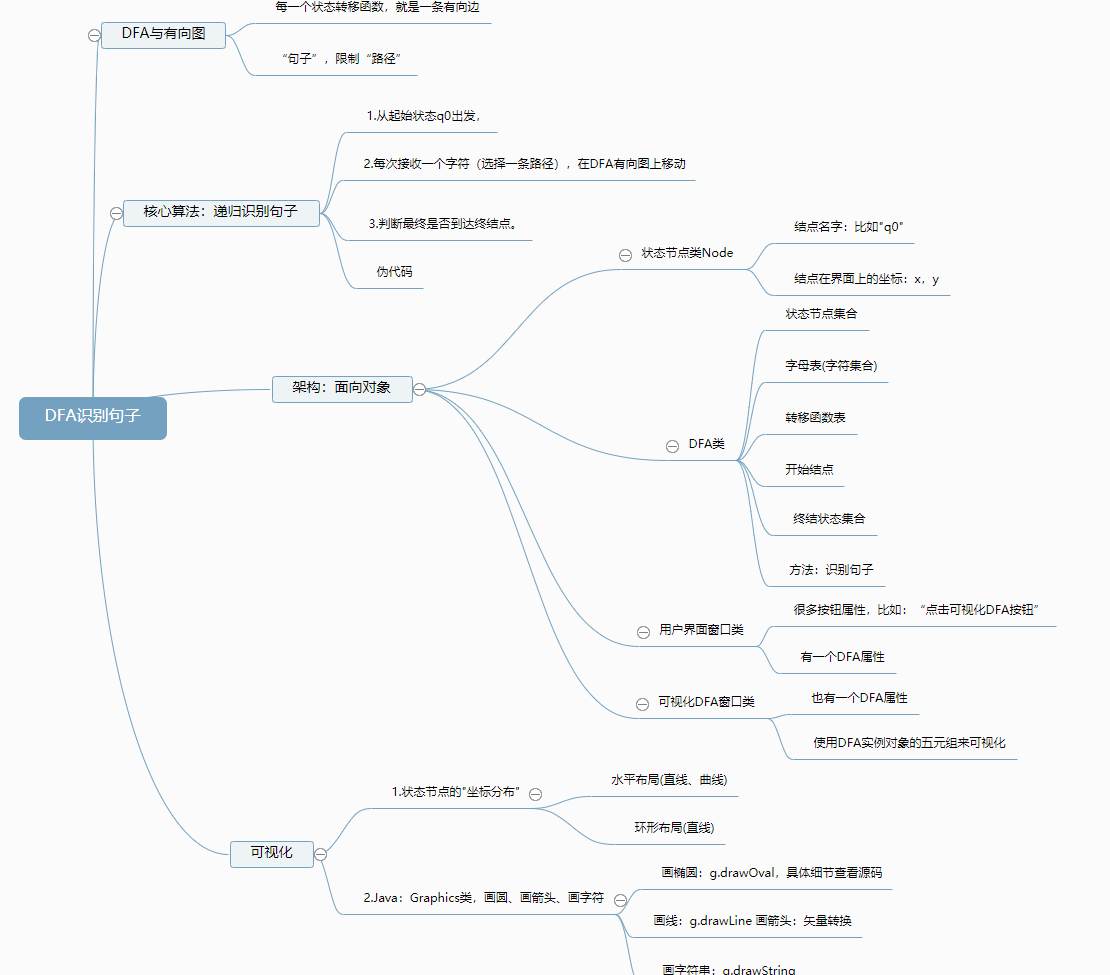
形式语言与自动机|DFA识别句子
实验二 DFA识别句子
一、实验目的
加深对DFA工作原理的理解。
二、实验内容
- 1.设计固定DFA。也就是说用if-then-else(一般用来实现字母表中只有两个字母的情况)、switch(大于两个字母的情况)、for(用于控制输入字符串,长度为n的字符串,for循环n次)等语句表示DFA。一个函数定义一个DFA;
- 2.设计文件形式存储DFA。设计文件格式,DFA动态生成,使用字符串来验证DFA的有效性和正确性;(使用面向对象的方法。对于k个状态的DFA,生成相应的k个状态对象;状态转换应通过对象间的消息传递来实现)
- 3.图形化表示。用java或者VC中图形功能实现图形化的dfa。(选作)
前置知识1:DFA
什么是FA,也叫有穷状态自动机;书上是这么说的👇,是一个五元组(状态集合,字母表,状态转移表,开始状态,终止状态集合)

什么是DFA,也是一个五元组,在FA的基础上加了一个**约束条件:每一个状态结点只能发出一条具有相同符号的边;也就是同一状态不能发出(输入字符相同的)两条边上。可以发出输入字符不同的多条边**
下图就是一个**DFA**栗子👇
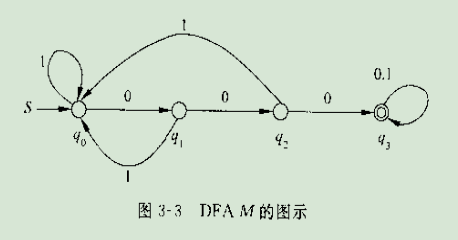
下图就是**NFA**的栗子👇(允许从一个状态发出多条具有相同符号的边,甚至允许发出标有ε(表示空)符号的边)
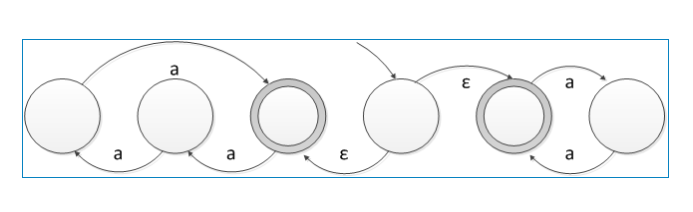
完成这个实验,只需要知道DFA就可以了。
前置知识2:有向图
什么是有向图:由顶点和有方向的边构成的图
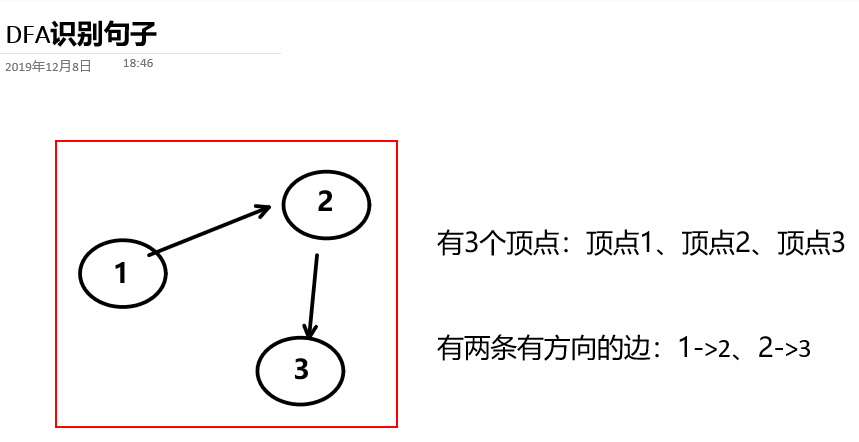
如何在程序中存储有向图?
可以使用数据结构中学的“邻接矩阵”
“邻接矩阵”就是一个“二维表”
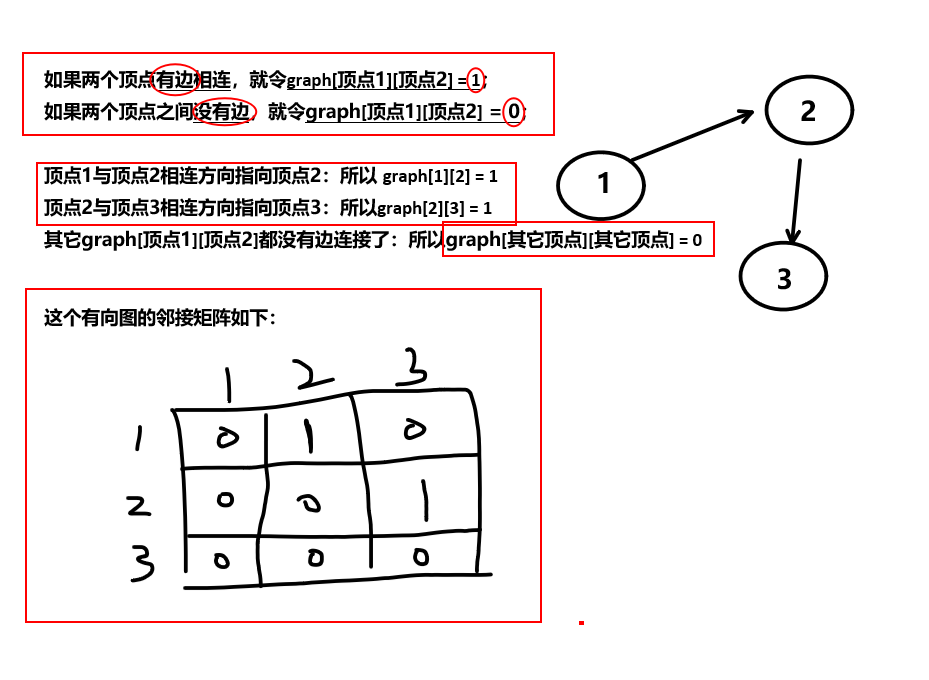
DFA实质就是一个有向图,各个顶点和其它顶点之间,使用有向边相连接;而DFA的状态转移表,就是它的邻接矩阵。
核心递归框架
。目的:DFA识别句子
先明晰目的:判断读入的句子是否能被我们设定的DFA识别
比如一个DFA功能是“识别偶数个0的句子”;那么读入句子“00”,偶数个0就能被识别,读入“000”,奇数个0就不能被识别。
什么情况下识别了句子:能到达终结点
什么情况下能被识别?:从初始状态读入一个句子,最终能到达终结状态结点,就是被识别了。
什么情况下不能被识别?:从初始状态读入一个句子,到最后到达非终结状态结点,就是不能被识别。
DFA的有向图上如何判断识别了句子?
“是否能被识别”,在DFA的有向图上如何表示?就是,从初始结点q0,一次读句子的一个字符,最终到达了终结状态。
还是那个栗子:识别偶数个0的DFA,假如我们输入的句子是 “00”👇
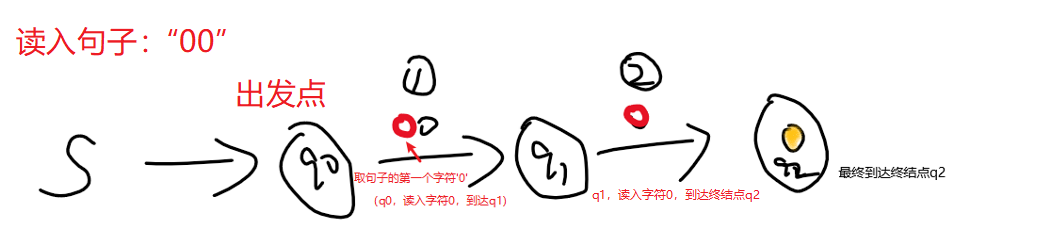
还是那个栗子:识别偶数个0的DFA,假如我们输入的句子是 “000”👇
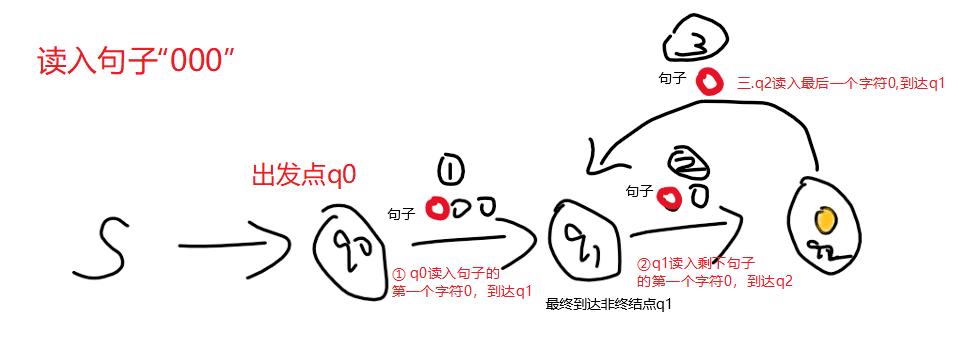
核心递归框架伪代码
下面两个方法都可以
第一种递归框架:递归参数:状态结点q1,读入的剩余句子字符
//递归参数:状态结点q1,读入的剩余句子字符
bool dfs(node 结点q1,string 句子sentence){
//1.递归出口:当句子为空 或者 句子长度为0的时候
if(sentence == NULL || sentence.length() == 0){
if(结点q1 是 终结点){
return true; //最后到达终结点;表示句子可以被这个dfa识别
}else{
return false; //否则 是非终结点;表示句子不能被这个dfa识别
}
}
//读入sentence的第一个字符后,到达新的状态结点q2
node q2 = 状态转移(q1,sentence[0]) //q1读入一个字符到达q2
return dfs(q2,"去除sentence第一个字符的剩下句子") //下一次递归参数: 结点q2,去除sentence第一个字符的剩下句子
}
把句子sentence设置为全局变量
第二种递归框架:递归参数:结点q1,当前读入的字符在"读入的句子"中的下标
//或者把句子sentence设置为全局变量
//下面一种递归思路,更换了递归参数,可能更容易理解
//递归参数:结点q1,当前读入的字符在"读入的句子"中的下标
bool dfs(node q1,int index){
//1.递归出口:当读入到句子的最后一个字符了,这时到达递归出口,判断转移后的结点是否是终结点
if(index == sentence.length() -1){
node q2 = 状态转移(q1,sentence[index]); //q1读入一个字符到达q2
if(结点q2 是 终结点){
return true; //最后到达终结点;表示句子可以被这个dfa识别
}else{
return false; //否则 是非终结点;表示句子不能被这个dfa识别
}
}
//状态转移 从q1读入字符sentence[indx] 到达q2
node q2 = 状态转移(q1,sentence[index]); //q1读入一个字符到达q2
return dfs(q2,index+1); //继续递归
}
开始写代码1.设计固定DFA
采用面向对象的方式编程,没有对象就new一个。
1-1:先写一个状态结点类
状态结点类的整体构造是这样的👇


1-2:DFA类
DFA的整体构造是这样的👇
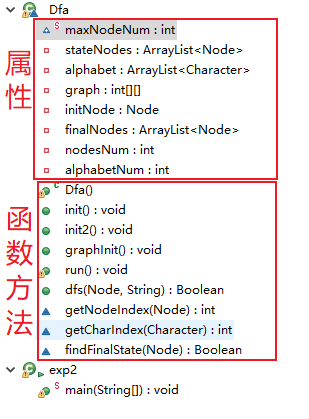
5元组对应5个属性,其它还应该有状态表结点个数、字母表字符个数、最大存储的结点个数等属性。👇
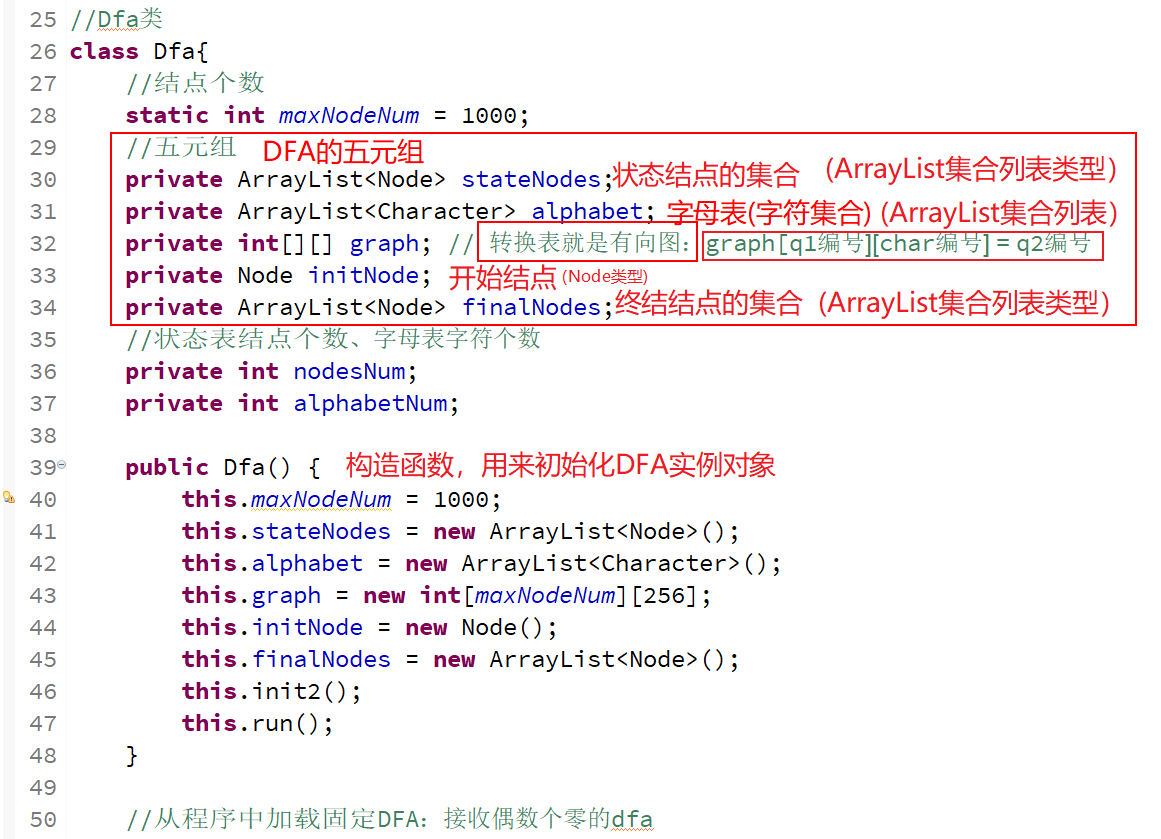
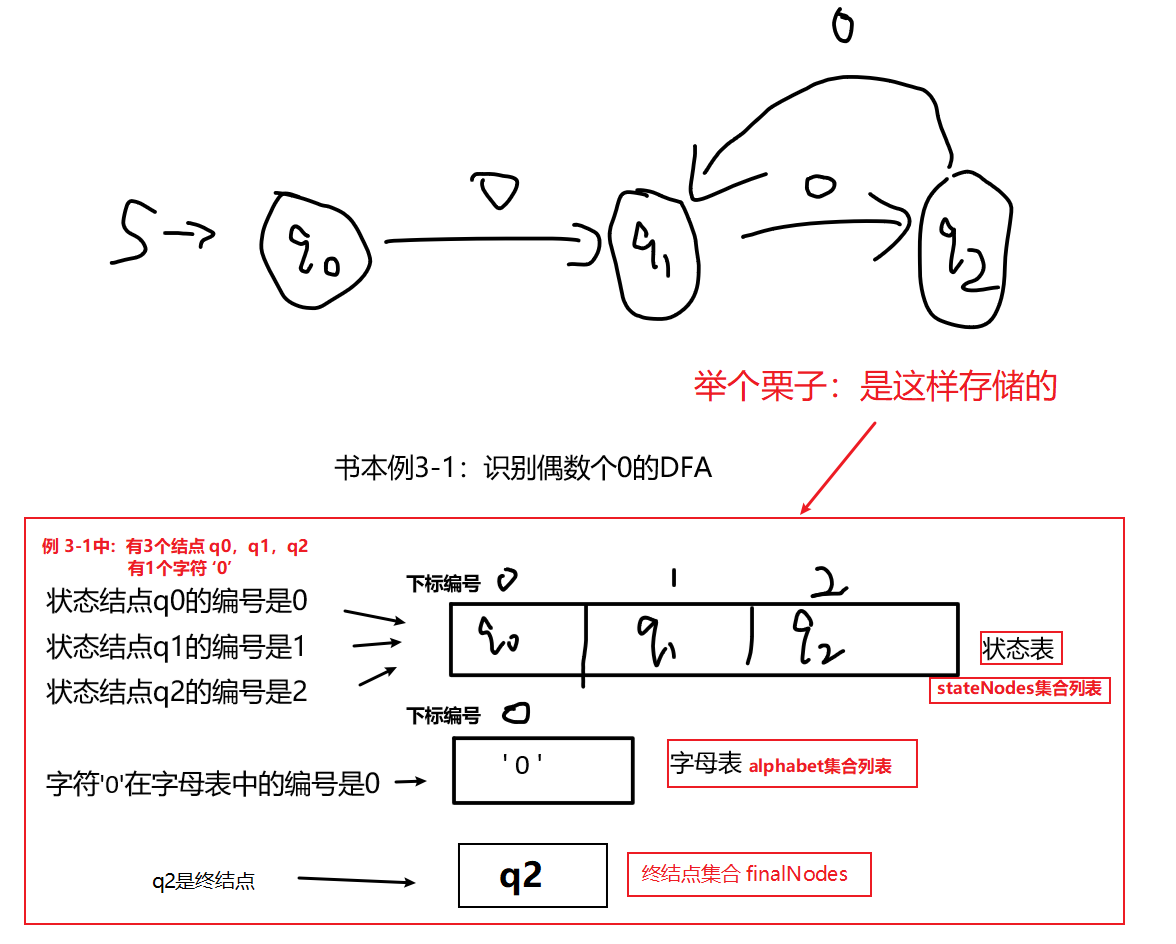
通过书上的一个DFA例子,理解一下状态集合、终结点集合、字母表集合是这样存储的👇
1-3:几个必要的函数


1-4:选一个栗子
选用例3-1 有穷自动机M: ({q0,q1,q2},{0},转换函数,q0,{q2}),作为样例
这个自动机功能是:识别偶数个0,比如00是合法的句子;而000就是非法的句子。
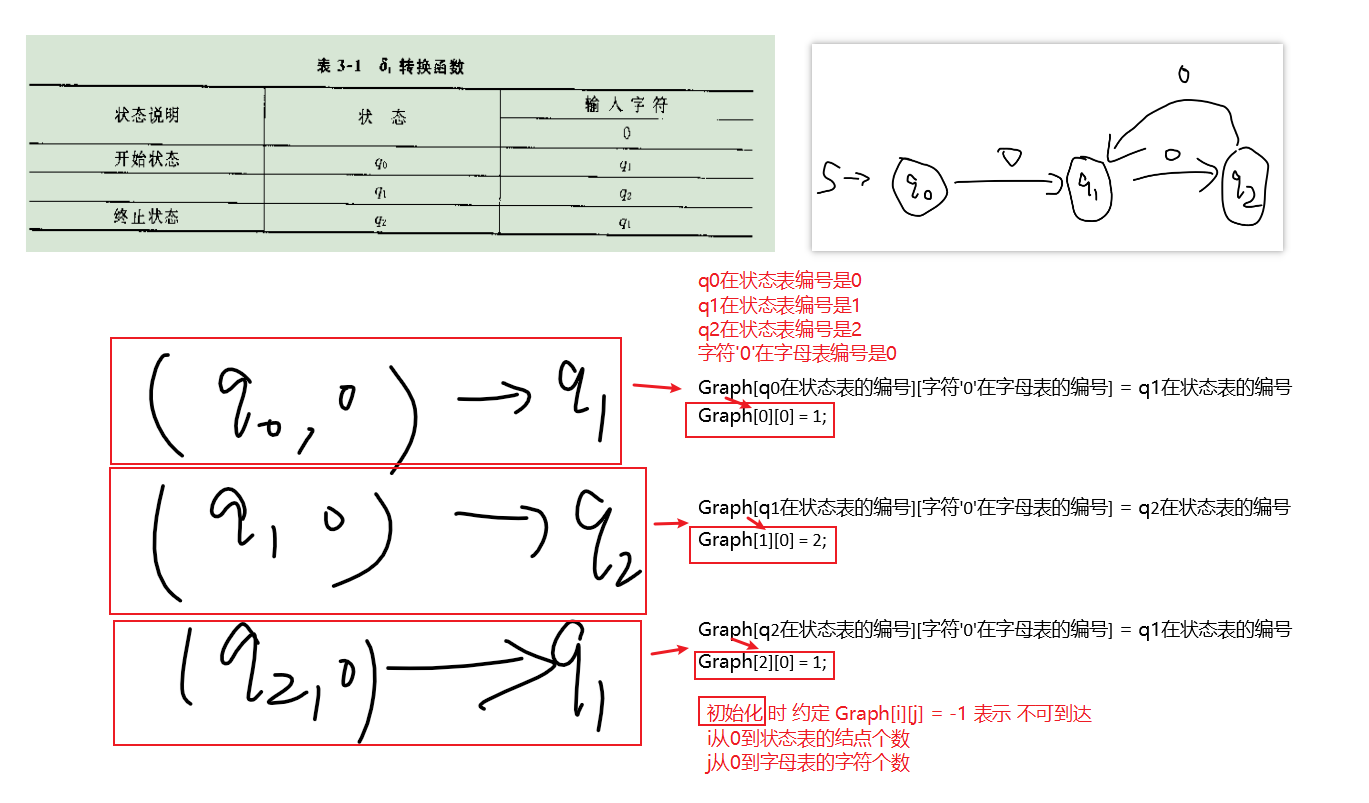
状态转换表如下
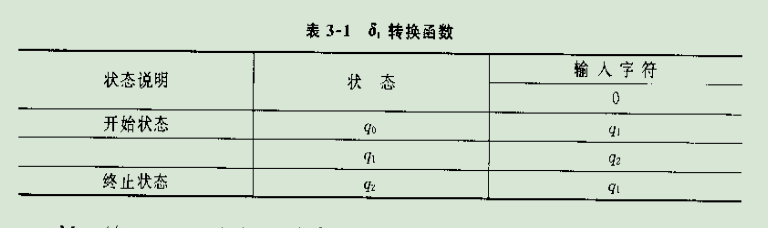
下图是例题3-1的DFA图👇
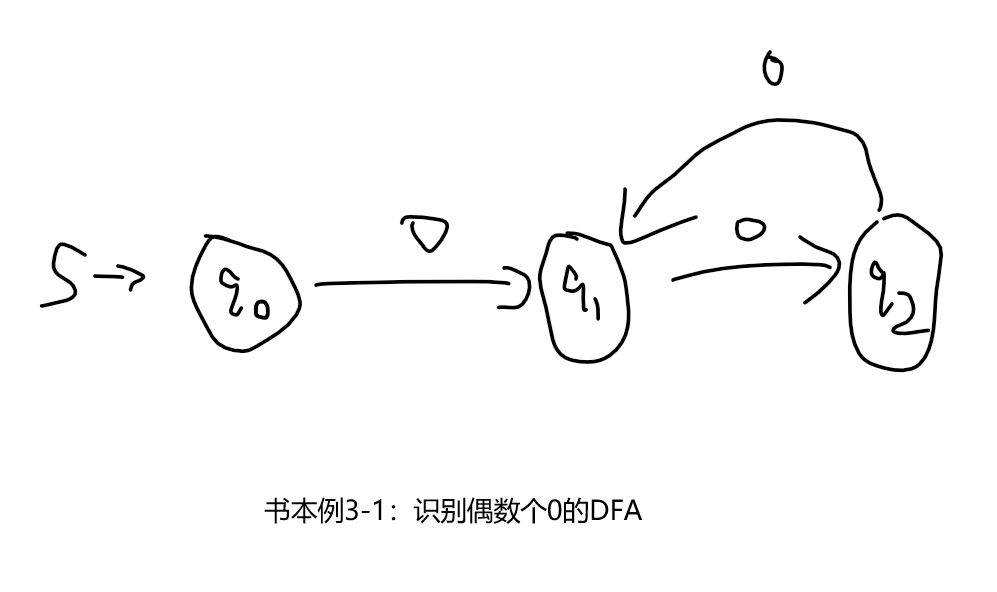
init()函数初始化例3-1的自动机👇,把例3-1的五元组分别存储到实例对象的5个属性中
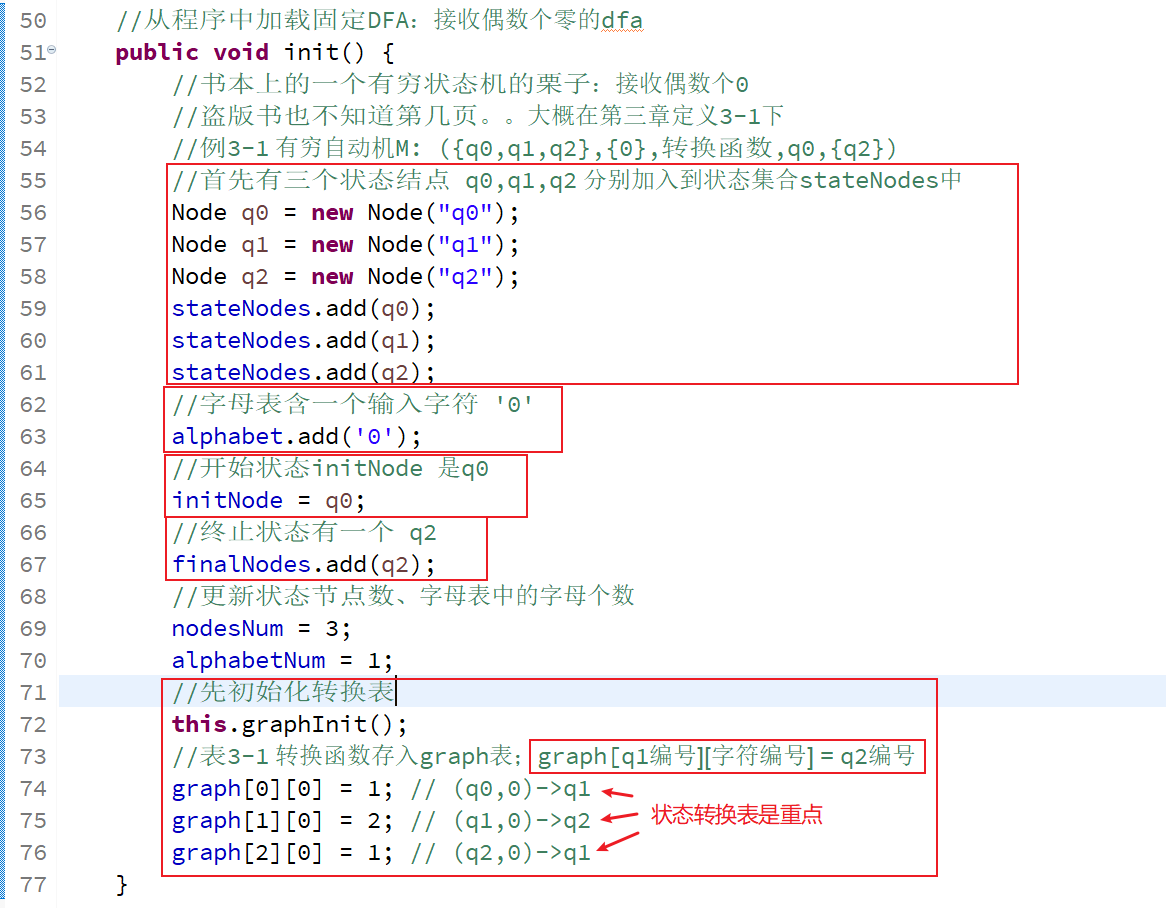
graphInit()函数初始化状态转换表
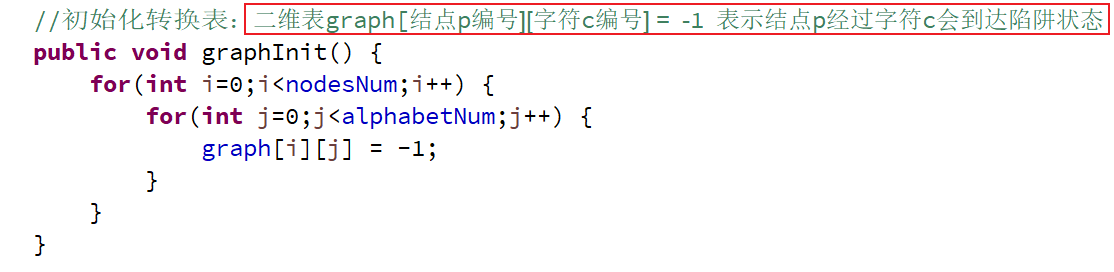
主要理解状态转换表(有向图的邻接矩阵)👇
状态集合、终结点集合、字母表集合是这样存储的👇

**然后试着理解状态转换表的存储**👇
1-5:核心,递归程序识别句子
**run()启动函数**👇

dfs()核心递归程序👇

1-6:例3-1栗子运行的效果
例3-1的DFA,功能:只识别偶数个0的句子。
主函数:

运行效果:
1-7:再举一个栗子,会不会更清楚一点
例3-3的DFA,**功能:识别末尾是000的句子。**比如:110000是能够识别正确的;而10100,因为末尾只有两个0所以无法识别
例3-3DFA如下图👇
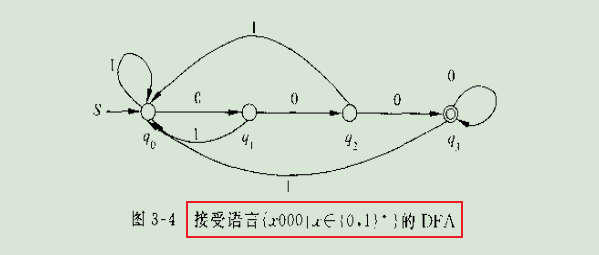
把例3-3的五元组,在计算机中存储,**“形式化”**,今天课上学到的名词。。还是动词??

对应在代码中就是这样的👇,修改init()函数,初始化DFA实例对象的五元组
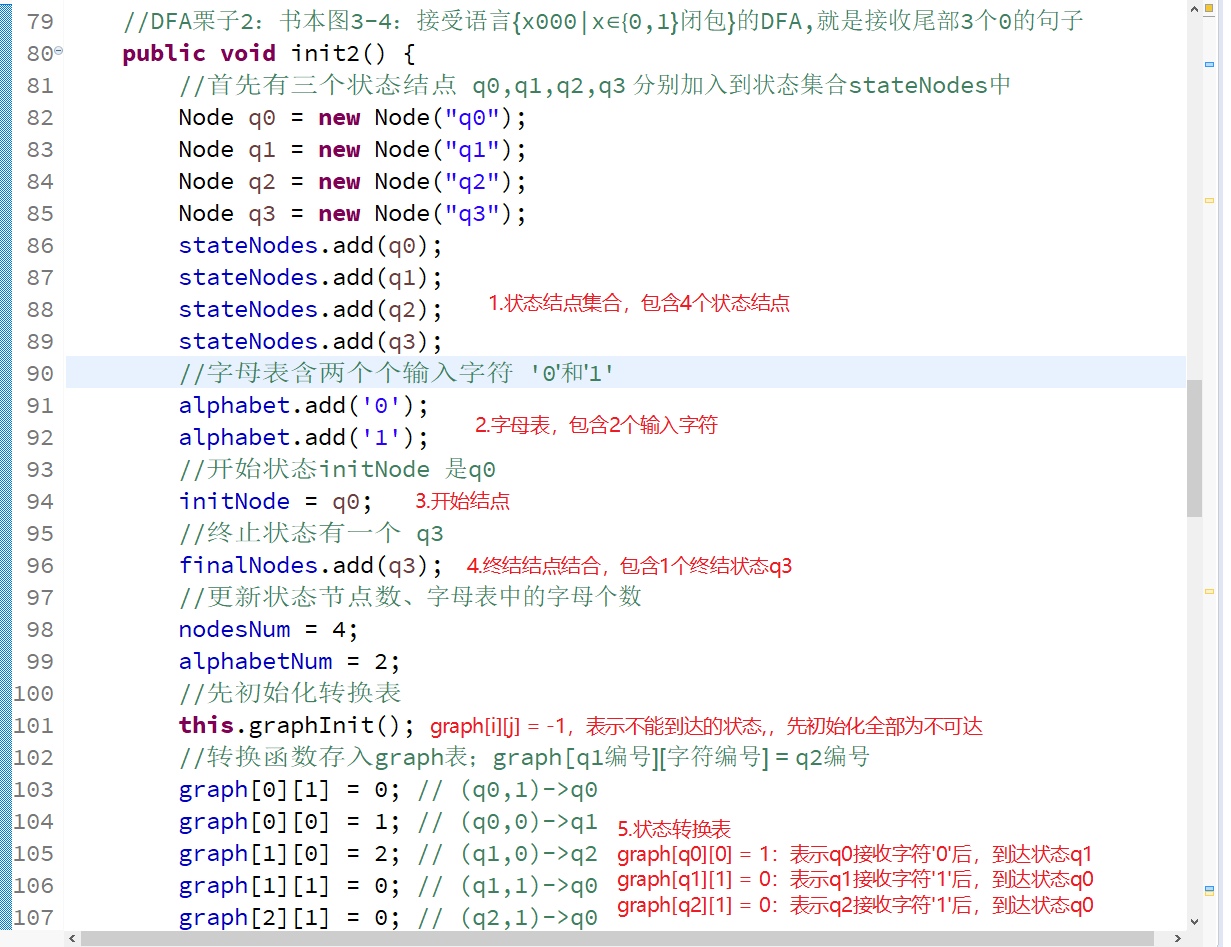

Main函数中创建DFA类的实例化对象,init2()函数读入例3-3的dfa五元组;再调用run()启动程序,输入要识别的句子即可。

###运行效果如下:
例3-3的DFA,功能:识别末尾是000的句子。
所以👇
输入句子'111000',识别成功

输入句子'10100',识别出错
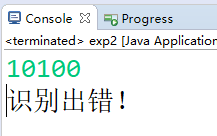
输入句子'101011000',识别成功
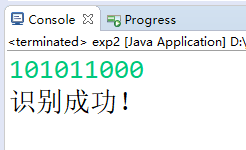
输入句子'1111',识别出错
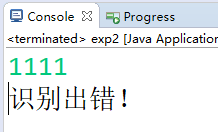
综上,实现了,一个函数对应一个固定DFA。
开始写代码2.文件形式存储DFA
步骤主要是这样的: * 1.从文件中读取每一行 * 2.把每一行,字符串处理,解析成五元组;比如,第一行是状态结点,就解析为结点,存储到状态结点集合中。 * 3.Main函数中运行run(),输入句子
我的文件里的五元组格式是这样的👇

字符串处理,比较繁琐,需要解析各个字符,读入到 DFA类的五元组中;当然如果文件存储的格式简单一点,就不用像我下面写的这样复杂了
每次读一行
这里用,(){}等等这些字符来分隔,状态节点、字符、转换函数
从文件中读入DFA的,仅供参考的 “从文件中读入DFA,存储dfa的五元组” 代码如下👇
public void loadFromFile(String path) {
File file = new File(this.path);
StringBuffer result = new StringBuffer();
List<String> resultList = new ArrayList<String>();
this.clear();
try {
BufferedReader bReader = new BufferedReader(new InputStreamReader(new FileInputStream(file),"UTF-8"));
String tempString = null;
while((tempString = bReader.readLine()) != null) {
resultList.add(tempString);
}
bReader.close();
String stateNodesString = resultList.get(0);
String alphabetString = resultList.get(1);
String initNodeString = resultList.get(2);
String finalString = resultList.get(3);
if(dealInputString(stateNodesString,0) == false) {
System.out.println("DFA有误!");
}
if(dealInputString(alphabetString,1) == false) {
System.out.println("DFA有误!");
}
if(dealInputString(initNodeString, 2) == false) {
System.out.println("DFA有误!");
}
if(dealInputString(finalString, 3) == false) {
System.out.println("DFA有误!");
}
if(dealFunction(resultList) == false) {
System.out.println("DFA有误!");
}
}catch (Exception e) {
System.out.println(e);
System.out.println("加载文件出错");
}
}
private Boolean dealFunction(List<String> resultList) {
//从resultList的第四行开始是 状态转移函数
this.graphInit();
if(resultList.size() <= 4) return false;
for(int i=4;i<resultList.size();i++) {
String function = resultList.get(i);
if(dealLine(function) == false) return false;
}
return true;
}
private Boolean dealLine(String function) {
StringBuffer currentBuffer = new StringBuffer();
int charIndex = -1;
int nodeIndex1 = -1;
int nodeIndex2 = -1;
for(int i=0;i<function.length();i++) {
if(function.charAt(i) == '(' ||function.charAt(i) == ')' || function.charAt(i) == '>' || function.charAt(i) == '-') {
currentBuffer.delete(0, currentBuffer.length());
}else if(function.charAt(i) == ',' ) {
//这里是第一个结点
nodeIndex1 = findNodeIndexByName(currentBuffer.toString());
if(nodeIndex1 == -1) return false;
currentBuffer.delete(0, currentBuffer.length());
}else if(i == function.length()-1) {
//这里是第二个结点
currentBuffer.append(function.charAt(i));
nodeIndex2 = findNodeIndexByName(currentBuffer.toString());
if(nodeIndex2 == -1) return false;
currentBuffer.delete(0, currentBuffer.length());
}else if(i>0 && function.charAt(i-1) == ','){
//这里是字符
Character c = function.charAt(i);
charIndex = getCharIndex(c);
if(charIndex == -1) return false;
}else {
currentBuffer.append(function.charAt(i));
}
}
if(nodeIndex1 == -1 || nodeIndex2 == -1 || charIndex == -1) return false;
this.graph[nodeIndex1][charIndex] = nodeIndex2;
System.out.println(stateNodes.get(nodeIndex1).getName()+"," + alphabet.get(charIndex) +" -> "+stateNodes.get(nodeIndex2).getName());
return true;
}
private void clear() {
// TODO Auto-generated method stub
this.stateNodes.clear();
this.alphabet.clear();
this.finalNodes.clear();
this.graphInit();
}
public boolean dealInputString(String s,int type) {
if(s == null) return false;
StringBuffer currentStateBuffer = new StringBuffer();
//type == 0时 处理的是 状态结点集合: 把输入的一行字符串转换为状态结点,并存入状态结点集合stateNodes中
if(type == 0) {
for(int i=0;i<s.length();i++) {
if(s.charAt(i) == '{') {
currentStateBuffer.delete(0, currentStateBuffer.length());
}else if(s.charAt(i) == ',' || s.charAt(i) == '}') {
this.stateNodes.add(new Node(currentStateBuffer.toString()));
currentStateBuffer.delete(0, currentStateBuffer.length());
}else {
currentStateBuffer.append(s.charAt(i));
}
}
this.nodesNum = stateNodes.size();
for(Node node: this.stateNodes) {
System.out.println(node.getName());
}
}else if(type == 1) {
for(int i=0;i<s.length();i++) {
if(s.charAt(i) == '{') {
continue;
}else if(s.charAt(i) == ',' || s.charAt(i) == '}') {
continue;
}else {
this.alphabet.add(s.charAt(i));
}
}
this.alphabetNum = alphabet.size();
for(Character c: this.alphabet) {
System.out.println(c);
}
}else if(type == 2) {
Node initNodeTemp = findNodeByName(s);
if(initNodeTemp == null) return false;
this.initNode = findNodeByName(s);
System.out.println(findNodeByName(s).getName());
}else if(type == 3) {
for(int i=0;i<s.length();i++) {
if(s.charAt(i) == '{') {
currentStateBuffer.delete(0, currentStateBuffer.length());
}else if(s.charAt(i) == ',' || s.charAt(i) == '}') {
Node finalNode = findNodeByName(currentStateBuffer.toString());
if(finalNode == null) return false;
this.finalNodes.add(finalNode);
currentStateBuffer.delete(0, currentStateBuffer.length());
}else {
currentStateBuffer.append(s.charAt(i));
}
}
for(Node node: this.finalNodes) {
System.out.println(node.getName());
}
}
return true;
}
public Node findNodeByName(String name) {
for(Node node : stateNodes) {
//node.getName() == name false:原因 == 用来判断引用
if(node.getName().equals(name))
return node;
}
return null;
}
public int findNodeIndexByName(String name) {
int i = 0;
for(Node node : stateNodes) {
//node.getName() == name false:原因 == 用来判断引用
if(node.getName().equals(name))
return i;
i++;
}
return -1;
}
运行效果和第一问相同:


3.图形化表示DFA
用Graphics类,重写paint方法,paint方法就是在窗口界面上画图。
详细可以参考这个链接,很简单但具体的栗子
这里用面向对象编程,就是写几个类,DFA类 与 状态结点类、窗口类各自执行自己的功能,数据和视图分离。