2019 蓝桥杯国赛 B 组模拟赛 题解
标签 ok

#include<bits/stdc++.h>
using namespace std;
/*
求阶乘 去除尾部0
每次求阶乘时:结果去除尾0,并对 1e6取余
*/
typedef long long ll;
ll n = 1325476;
const ll mod = 1e6;
ll ans = 1;
void solve(){
while(ans%10 == 0) ans = ans/10;
ans = ans%mod;
}
int main(){
for(ll i = n;i>=1;i--){
ans = ans * i;
solve();
}
printf("%lld",ans);
return 0;
}
//137664
#include<bits/stdc++.h>
using namespace std;
/*
2 * 5会产生0
做法:每次循环求阶乘时 统计2和5个数 并去除2和5,最后乘回来即可
*/
typedef long long ll;
ll n = 1325476;
const ll mod = 1e6;
ll ans = 1;
ll cnt1 = 0;
ll cnt2 = 0;
int main(){
for(ll i = 1;i <= n; i++){
ll x = i;
while(x%2==0) cnt1++,x=x/2;
while(x%5==0) cnt2++,x=x/5;
ans = ans * x % mod;
}
if(cnt1 - cnt2 > 0){
for(int i=1;i<=cnt1-cnt2;i++) ans = ans * 2 % mod;
}else{
for(int i=1;i<=cnt2-cnt1;i++) ans = ans * 5 % mod;
}
printf("%lld\n",ans);
return 0;
}
//137664
101串 ok

dfs搜索方法
#include<bits/stdc++.h>
using namespace std;
int num[35];
long long ans = 0;
/*
dfs枚举2^30种可能结果
运行100秒左右
*/
void dfs(int k){
if(k==31){
for(int i=1;i<=28;i++){
if(num[i] == 1 && num[i+1] == 0 && num[i+2] == 1){
ans++;
break;
}
}
return;
}
num[k] = 1;
dfs(k+1);
num[k] = 0;
dfs(k+1);
}
int main(){
dfs(1);
printf("%lld",ans);
return 0;
}
//1046810092
二进制枚举方法
#include<bits/stdc++.h>
using namespace std;
/*
二进制枚举
1<<30种 也就是2^30可能情况
对于每个情况 枚举每一位 判断是否满足条件
*/
int ans = 0;
int main(){
for(int i=0;i<(1<<30);i++){
int x = i;
int a = 0 ,b = 0, c = 0;
bool check = false;
while(x){
c = b;
b = a;
a = x & 1;
if(a && !b && c){
check = true;
break;
}
x >>= 1;
}
if(check) ans++;
}
cout<<ans<<endl;
return 0;
}
//1046810092
游戏 ok


#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL a = 482333897982347239LL;
LL b = 557432748293424892LL;
LL k = 1389472389742429877LL;
//同余 (b-a) % mod = b*2 % mod
void test(){
LL mod = a + b;
cout<<(b-a) % mod<<endl;
cout<<b*2%mod<<endl;
}
//快速乘:加法代替乘法
LL mmul(LL x,LL y,LL p){
LL ans = 0LL;
while(y){
if( y & 1LL) ans = (ans + x) % p;
x = (x + x) % p;
y >>= 1;
}
return ans;
}
//快速幂
LL mpow(LL x,LL y,LL p){
LL ans = 1LL;
while(y){
if(y & 1LL) ans = mmul(ans,x,p);
x = mmul(x,x,p);
y >>= 1;
}
return ans;
}
int main(){
LL mod = a + b; //首先 c + d = 2*a + b - a = a + b = mod
LL ans = mmul(a,mpow(2LL,k,mod),mod); //d = b - a = b - (mod - b) = 2*b - mod = 2*b %mod,所以 b-a 也就等价于 b*2,等价后a与b交不交换都无所谓(因为后面的操作都是*2)
printf("%lld\n",min(ans,mod-ans));//结果确保A更小,A可能是ans 也可能是mod-ans(b)
return 0;
}
//383513242709218605
公约数 ok
蒜头君有n个数,他想要从中选出k个数,使得它们的最大公约数最大。
请你求出这个最大的最大公约数。
输入格式
第一行输入两个整数 。
第二行输入 个整数 。
输出格式
输出一个整数。
数据范围
样例输入1
4 3
2 4 8 3
样例输出1
2
样例输入2
4 2
4 8 6 6
样例输出1
6
思路:
30% 暴力dfs 或者 状态压缩(二进制枚举)选出k个数
另外30% 由概率,直接输出 1。
100% 枚举可能的gcd 值,检查有多少元素被它整除即可。时间复杂度O(nlogn)
30%代码-dfs搜索
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans = 1;
ll gcd(ll a,ll b){
if(b==0)
return a;
return gcd(b,a%b);
}
const int maxn = 1e6+10;
int n,k;
int a[maxn];
/*
dfs暴搜过30%数据
*/
/*
不确定的dp状态转移方程:dp[i][k] = max(dp[i][k],gcd(dp[j<i][k-1], a[i])
*/
void dfs(int cur,int have,ll _gcd){
if(cur == n+1 && have == k+1){
ans = max(ans,_gcd);
return;
}
if(cur > n+1) return;
if(have > k+1) return;
if(have == 1){
dfs(cur+1,have,_gcd);
dfs(cur+1,have+1,a[cur]);
}else{
dfs(cur+1,have,_gcd);
dfs(cur+1,have+1,gcd(a[cur],_gcd));
}
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
dfs(1,1,0);
printf("%lld\n",ans);
return 0;
}
100%代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 7;
const int mod = 1e9 + 7;
int a[N+10];
int main(){
int n,k,x;
memset(a,0,sizeof(a));
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++){
scanf("%d",&x);
a[x]++;//x的个数+1
}
int ans = 1;
//枚举gcd可能出现的值:从i=2 ~ N;
for(int i = 2 ;i < N; i++){
int cnt = 0;
for(int j = i;j < N; j += i) cnt += a[j]; //能被i整除的数 一定是 i i+i i+i+i ....
if(cnt >= k) ans = i;//比k大 那么选出k个数 他们的gcd就是当前的i
}
printf("%d\n",ans);
return 0;
}
蒜头图 ok

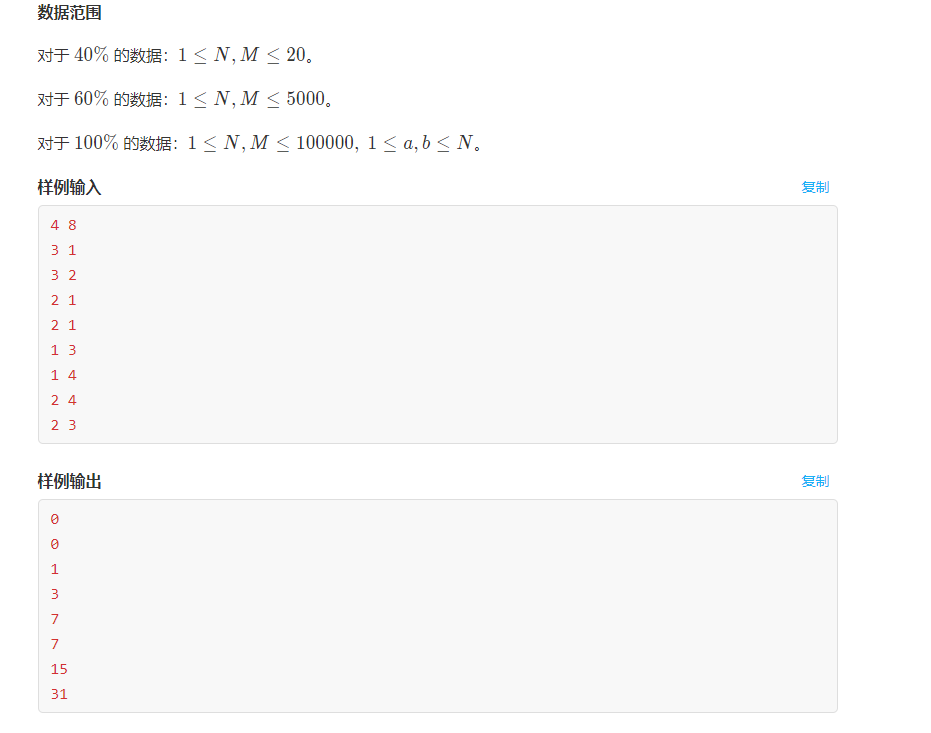
实际上就是问图里有多少个环,计环的个数为 k,则结果为2^k-1。
30% 状态压缩选出边,判断所选的边是否构成环
100% 并查集统计环的数量,使用并查集每次询问只需要判断这两点之前是否连通就可以了,为什么结果是2^k-1呢(k表示环的数量),有大佬说了:题目表明了“只要构成蒜头图就算一种情况”,那么也就是说从原图中取1个环也能构成环,取其中两个环也能构成环(有环就代表是蒜头图的子图,管你取几个环都是蒜头图).......C(n,i) i从1~n都能构成环 那么C(n,1) + C(n,2) + C(n,3) + C(n,n)就是答案,这个式子的值也等于2^n-1,因为C(n,0) + C(n,1) + C(n,2) + C(n,3) + C(n,n) 的结果等于2^n
100%代码-并查集统计环的数量
#include<bits/stdc++.h>
using namespace std;
const int mod = 1046513837;
int n,m,f[200500];
int find(int x){
return f[x] == x ? x : f[x] = find(f[x]);
}
void merge(int a,int b){
int x = find(a);
int y = find(b);
if(x != y ) f[x] = y;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) f[i] = i;
long long ans = 1;
for(int i=1 ;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
int x = find(a), y = find(b);
if(x == y){//这里如果 两个点祖先一样 说明找到环了
ans <<= 1;
if(ans > mod) ans -= mod;
}else merge(a,b);
printf("%lld\n",ans-1);
}
return 0;
}
区间并 60% 线段树做法不会

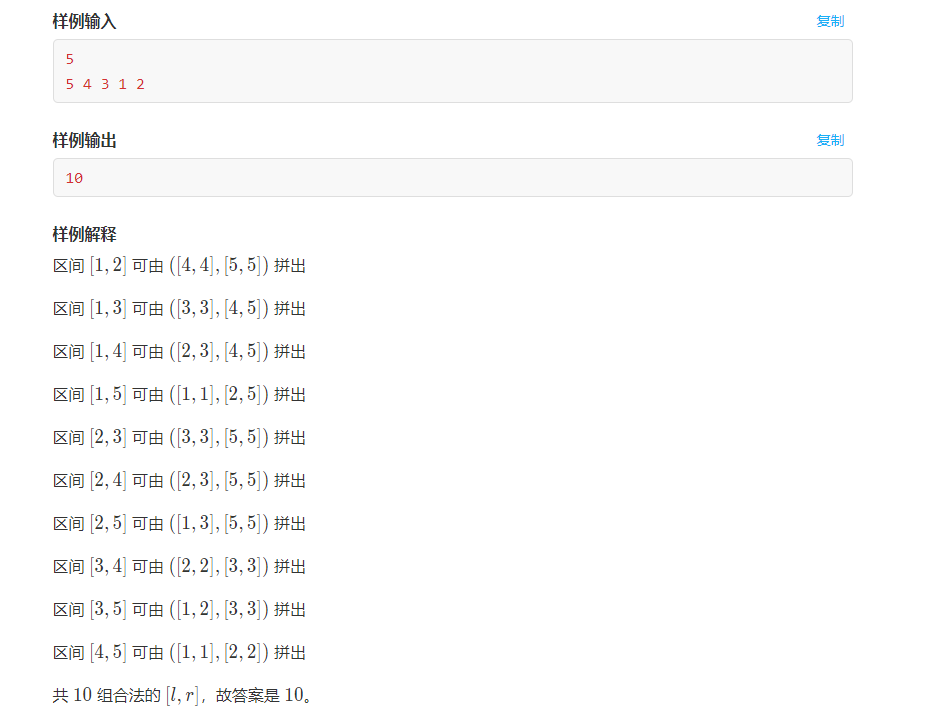
30% 按照题意暴力计算,枚举权值区间,枚举给定的数组的区间 ok
60% 枚举所有的答案区间l~r,看看哪些区间能恰好分成两个不相交的区间,暴力做的话:枚举l和r共O(n2),加上判断是否恰好分成了两个区间共O(n3)。判断是否分成了两个区间可以用并查集来维护,查询复杂度可以降到O(1)。
具体怎么用并查集维护?没写代码,但我是这样想的,在原序列中 如果 a[i] 和 a[i-1] 是连续的 即(后面这个数比前面这个数值大1) 就把当前第i个数 加入第i-1的集合中,代表他们是一个区间的。后面查询是否分成两个区间时,只需查询l~r区间内的数被分成了几个集合就可以了。
这个思路我自认为没有问题emmmm
100% 线段树维护区间最大值、次大值、相应个数 O(nlogn) 不会
30%代码-暴力枚举:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 3*1e6+5;
int n;
int m[maxn];
int vis[maxn];
int ans = 0;
/*
枚举l~r区间
枚举i~j区间
*/
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&m[i]);
for(int l=1;l<=n;l++){
for(int r=l+1;r<=n;r++){
bool flag = false;
for(int a=1;a<=n;a++){
for(int b=a;b<=n;b++){
for(int c=b+1;c<=n;c++){
for(int d=c;d<=n;d++){
bool flag2 = true;
for(int i=1;i<=n;i++) vis[i] = 0;
for(int i=a;i<=b;i++) vis[m[i]] = 1;
for(int i=c;i<=d;i++) vis[m[i]] = 1;
for(int i=l;i<=r;i++){
if(vis[i] == 0){
flag2 = false;
break;
}
}
if(flag2 && r-l+1 == b-a+1 + d-c+1){
ans++;
flag = true;
//cout<<"l = "<<l<<" r = "<<r<<"a = "<<a<<" b = "<<b<<" c = "<<c<<" d = "<<d<<endl;
break;
}
if(flag) break;
}
if(flag) break;
}
if(flag) break;
}
if(flag) break;
}
// if(flag) continue;
}
}
cout<<ans<<endl;
return 0;
}
/*
5
5 4 3 1 2
*/
100%代码-线段树
#include<cstdio>
#include<algorithm>
#define mid (l+r)/2
#define lt (s<<1)
#define rt (s<<1|1)
#define Mn 300005
using namespace std;
long long ans;
int fc[Mn*4],fm[Mn*4],sm[Mn*4],sc[Mn*4];
int p[Mn],nt[Mn],add[Mn*4],n,i,k1,k2,x;
void updata(int s)
{
int k1=lt,k2=rt;
if (fm[k1]>fm[k2]) swap(k1,k2);
if (fm[k1]<fm[k2])
{
fm[s]=fm[k1],fc[s]=fc[k1];
if (sm[k1]<fm[k2])
sm[s]=sm[k1],sc[s]=sc[k1];
else
if (sm[k1]==fm[k2])
sm[s]=sm[k1],sc[s]=sc[k1]+fc[k2];
else sm[s]=fm[k2],sc[s]=fc[k2];
}
if (fm[k1]==fm[k2])
{
fm[s]=fm[k1],fc[s]=fc[k1]+fc[k2];
if (sm[k1]<sm[k2])
sm[s]=sm[k1],sc[s]=sc[k1];
else
if (sm[k2]<sm[k1])
sm[s]=sm[k2],sc[s]=sc[k2];
else sm[s]=sm[k2],sc[s]=sc[k1]+sc[k2];
}
}
void pplus(int s,int up)
{
fm[s]+=up; sm[s]+=up;
add[s]+=up;
}
void push(int s)
{
if (add[s]!=0)
pplus(lt,add[s]),pplus(rt,add[s]),add[s]=0;
}
void work(int s,int l,int r,int ls,int rs,int up)
{
if (l>rs || r<ls) return;
if (ls<=l && r<=rs)
return(void)(pplus(s,up));
push(s);
work(lt,l,mid,ls,rs,up);
work(rt,mid+1,r,ls,rs,up);
updata(s);
}
void build(int s,int l,int r)
{
if (l==r) return(void)(fc[s]=1,sm[s]=1);
build(lt,l,mid); build(rt,mid+1,r);
updata(s);
}
void upans(int s,int l,int r,int ls,int rs)
{
if (ls<=l && r<=rs)
{
if (fm[s]==1 || fm[s]==2) ans+=fc[s];
if (sm[s]==1 || sm[s]==2) ans+=sc[s];
return;
}
if (ls>r || l>rs) return;
push(s);
upans(lt,l,mid,ls,rs);
upans(rt,mid+1,r,ls,rs);
updata(s);
}
int main()
{
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d",&p[i]),nt[p[i]]=i;
build(1,1,n);
for(i=n;i>=1;i--)
{
x=nt[i];
if (p[x+1]<i && p[x-1]<i) work(1,1,n,i,n,1);
if (p[x+1]<i && p[x-1]>i) work(1,1,n,i,p[x-1]-1,1);
if (p[x+1]>i && p[x-1]<i) work(1,1,n,i,p[x+1]-1,1);
if (p[x+1]>i && p[x-1]>i)
{
k1=p[x+1]; k2=p[x-1];
if (k1>k2) swap(k1,k2);
work(1,1,n,i,k1-1,1);
work(1,1,n,k2,n,-1);
}
upans(1,1,n,i,n);
}
printf("%lld",ans-n);
return 0;
}