2018年天梯赛LV2题目汇总小结
Ⅰ.L2-1 分而治之---邻接表
分而治之,各个击破是兵家常用的策略之一。在战争中,我们希望首先攻下敌方的部分城市,使其剩余的城市变成孤立无援,然后再分头各个击破。为此参谋部提供了若干打击方案。本题就请你编写程序,判断每个方案的可行性。
输入格式:
输入在第一行给出两个正整数 N 和 M(均不超过10 000),分别为敌方城市个数(于是默认城市从 1 到 N 编号)和连接两城市的通路条数。随后 M 行,每行给出一条通路所连接的两个城市的编号,其间以一个空格分隔。在城市信息之后给出参谋部的系列方案,即一个正整数 K (≤ 100)和随后的 K 行方案,每行按以下格式给出:
Np v[1] v[2] ... v[Np]
其中 Np 是该方案中计划攻下的城市数量,后面的系列 v[i] 是计划攻下的城市编号。
输出格式:
对每一套方案,如果可行就输出YES,否则输出NO。
输入样例:
10 11
8 7
6 8
4 5
8 4
8 1
1 2
1 4
9 8
9 1
1 10
2 4
5
4 10 3 8 4
6 6 1 7 5 4 9
3 1 8 4
2 2 8
7 9 8 7 6 5 4 2
输出样例:
NO
YES
YES
NO
NO
思路:阅读理解,画画图还是能想到的,考的是邻接表。
城市被攻破孤立,意思就是结点没有邻接点了,它原来的邻接点都被攻打了,只需要用数组统计邻接边的数量,或者集合统计是否一条边的两个顶点都被攻打了
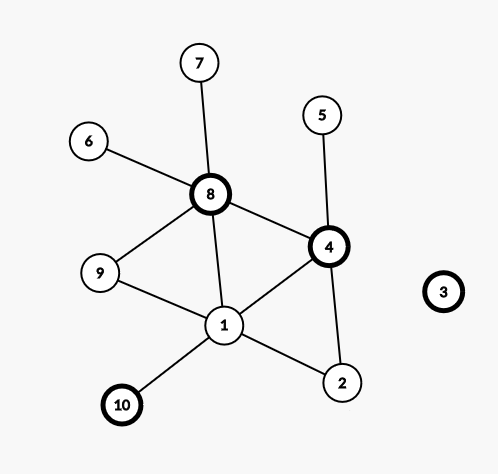
#include<bits/stdc++.h>
using namespace std;
/*
edge数组中存入边
对于每一个方案,将攻打的城市节点存入set集合中,查询m条边如果边对应的两个点都没被攻打 说明这条边完整-->两个城市节点是连通的(方案不可行
*/
int edge[10010][2];
set<int> se;
int n,m,k;
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>edge[i][0];
cin>>edge[i][1];
}
cin>>k;
for(int i=1;i<=k;i++){
int np;
cin>>np;
for(int j=1;j<=np;j++){
int city;
cin>>city;
se.insert(city);
}
bool flag = true;
for(int j=1;j<=m;j++){
if(se.find(edge[j][0]) == se.end() && se.find(edge[j][1]) == se.end()){
flag = false;
break;
}
}
if(flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
se.clear();
}
return 0;
}
Ⅱ.L2-2 小字辈 ---树的深度
本题给定一个庞大家族的家谱,要请你给出最小一辈的名单。
输入格式:
输入在第一行给出家族人口总数 N(不超过 100 000 的正整数) —— 简单起见,我们把家族成员从 1 到 N 编号。随后第二行给出 N 个编号,其中第 i 个编号对应第 i 位成员的父/母。家谱中辈分最高的老祖宗对应的父/母编号为 -1。一行中的数字间以空格分隔。
输出格式:
首先输出最小的辈分(老祖宗的辈分为 1,以下逐级递增)。然后在第二行按递增顺序输出辈分最小的成员的编号。编号间以一个空格分隔,行首尾不得有多余空格。
输入样例:
9
2 6 5 5 -1 5 6 4 7
输出样例:
4
1 9
思路:画出图,就是一颗树,
方法一:路径压缩;方法二:bfs从根出发层次遍历;方法三dfs从根深搜,统计等级(到根的距离)
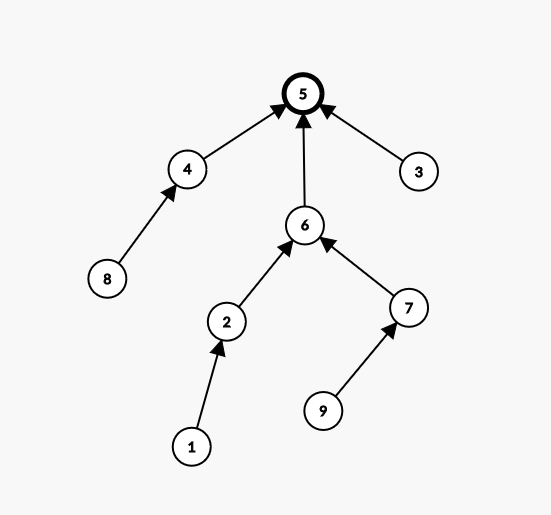
bfs做法:从根出发层次遍历,统计等级
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100010;
int n;
vector<int> g[maxn];
vector<int> u[maxn];
int vis[maxn];
int maxrank = 1;
struct node{
int v;
int rank;
node(int xx,int rankk){
v = xx;
rank = rankk;
}
};
void bfs(int s){
queue<node> q;
q.push(node(s,1));
while(!q.empty()){
int curv = q.front().v;
int currank = q.front().rank;
u[currank].push_back(curv);
q.pop();
if(currank > maxrank) maxrank = currank;
vis[curv] = 1;
for(int i=0;i<g[curv].size();i++){
if(!vis[g[curv][i]]){
q.push(node(g[curv][i],currank+1));
}
}
}
}
int main(){
cin>>n;
int root = 1;
int v;
for(int i=1;i<=n;i++){
cin>>v;
g[v].push_back(i);
if(v==-1){
root = i;
}
}
bfs(root);
cout<<maxrank<<endl;
int first = 1;
for(int i=0;i<u[maxrank].size();i++){
if(first){
first = 0;
cout<<u[maxrank][i];
}else{
cout<<" "<<u[maxrank][i];
}
}
return 0;
}
Ⅲ.L2-3 名人堂与代金券---sort排序重载
对于在中国大学MOOC(http://www.icourse163.org/ )学习“数据结构”课程的学生,想要获得一张合格证书,总评成绩必须达到 60 分及以上,并且有另加福利:总评分在 [G, 100] 区间内者,可以得到 50 元 PAT 代金券;在 [60, G) 区间内者,可以得到 20 元PAT代金券。全国考点通用,一年有效。同时任课老师还会把总评成绩前 K 名的学生列入课程“名人堂”。本题就请你编写程序,帮助老师列出名人堂的学生,并统计一共发出了面值多少元的 PAT 代金券。
输入格式:
输入在第一行给出 3 个整数,分别是 N(不超过 10 000 的正整数,为学生总数)、G(在 (60,100) 区间内的整数,为题面中描述的代金券等级分界线)、K(不超过 100 且不超过 N 的正整数,为进入名人堂的最低名次)。接下来 N 行,每行给出一位学生的账号(长度不超过15位、不带空格的字符串)和总评成绩(区间 [0, 100] 内的整数),其间以空格分隔。题目保证没有重复的账号。
输出格式:
首先在一行中输出发出的 PAT 代金券的总面值。然后按总评成绩非升序输出进入名人堂的学生的名次、账号和成绩,其间以 1 个空格分隔。需要注意的是:成绩相同的学生享有并列的排名,排名并列时,按账号的字母序升序输出。
输入样例:
10 80 5
cy@zju.edu.cn 78
cy@pat-edu.com 87
1001@qq.com 65
uh-oh@163.com 96
test@126.com 39
anyone@qq.com 87
zoe@mit.edu 80
jack@ucla.edu 88
bob@cmu.edu 80
ken@163.com 70
输出样例:
360
1 uh-oh@163.com 96
2 jack@ucla.edu 88
3 anyone@qq.com 87
3 cy@pat-edu.com 87
5 bob@cmu.edu 80
5 zoe@mit.edu 80
思路:结构体每个人的账号和分数,重载sort排序,排出等级(并列)
其他参考代码:https://blog.csdn.net/caipengbenren/article/details/87791719
#include<bits/stdc++.h>
using namespace std;
struct stu{
string name;
int score;
};
//排序 先按分数再按字典序
bool cmp(stu a,stu b){
if(a.score == b.score){
return a.name < b.name;
}
return a.score > b.score;
}
stu s[10010];
int n,g,k;
int main(){
cin>>n>>g>>k;
for(int i=0;i<n;i++){
cin>>s[i].name;
cin>>s[i].score;
}
sort(s,s+n,cmp);
int sum = 0;
for(int i=0;i<n;i++){
if(s[i].score >=g && s[i].score <=100){
sum += 50;
}else if(s[i].score >=60 && s[i].score <g){
sum += 20;
}
}
cout<<sum<<endl;
int t = 0;
for(int i=0;i<n;i++){
if(t>=k)break;
cout<<t+1<<" "<<s[i].name<<" "<<s[i].score<<endl;
int d = t;
for(int j=i+1;j<n;j++){
if(s[i].score == s[j].score){
cout<<t+1<<" "<<s[j].name<<" "<<s[j].score<<endl;
d++;
i++;
}else{
break;
}
}
t = d;
t++;
}
return 0;
}
Ⅳ.L2-4 秀恩爱分得快---数据存放(STL)
古人云:秀恩爱,分得快。
互联网上每天都有大量人发布大量照片,我们通过分析这些照片,可以分析人与人之间的亲密度。如果一张照片上出现了 K 个人,这些人两两间的亲密度就被定义为 1/K。任意两个人如果同时出现在若干张照片里,他们之间的亲密度就是所有这些同框照片对应的亲密度之和。下面给定一批照片,请你分析一对给定的情侣,看看他们分别有没有亲密度更高的异性朋友?
输入格式:
输入在第一行给出 2 个正整数:N(不超过1000,为总人数——简单起见,我们把所有人从 0 到 N-1 编号。为了区分性别,我们用编号前的负号表示女性)和 M(不超过1000,为照片总数)。随后 M 行,每行给出一张照片的信息,格式如下:
K P[1] ... P[K]
其中 K(≤ 500)是该照片中出现的人数,P[1] ~ P[K] 就是这些人的编号。最后一行给出一对异性情侣的编号 A 和 B。同行数字以空格分隔。题目保证每个人只有一个性别,并且不会在同一张照片里出现多次。
输出格式:
首先输出 A PA,其中 PA 是与 A 最亲密的异性。如果 PA 不唯一,则按他们编号的绝对值递增输出;然后类似地输出 B PB。但如果 A 和 B 正是彼此亲密度最高的一对,则只输出他们的编号,无论是否还有其他人并列。
输入样例 1:
10 4
4 -1 2 -3 4
4 2 -3 -5 -6
3 2 4 -5
3 -6 0 2
-3 2
输出样例 1:
-3 2
2 -5
2 -6
输入样例 2:
4 4
4 -1 2 -3 0
2 0 -3
2 2 -3
2 -1 2
-3 2
输出样例 2:
-3 2
思路:
我们只需要分别更新 给出的pa和pb两人的亲密度(无需在输入时每个人都去更新一遍)
vector<vector<int> > p:存照片上的数据(每张照片上有哪些人)
vector<double> pa pb: 存放与a/b有关系的人的亲密度
遍历一遍所有照片 如果包含a/b就更新与a/b是异性关系的亲密度
判断a和b是否分别为对方亲密度最高值 按题目要求输出结果
代码转载至:https://blog.csdn.net/wsxyh1071652438/article/details/82115346
#include<bits/stdc++.h>
using namespace std;
bool gender[1000]={0}; //gender[person-id]=if-is-a-girl, 1 for girl, 0 for boy
int read(){
int input=0, flag=0;
char a=getchar();
while((a<'0' || a>'9') && a!='-')
a=getchar();
if(a=='-'){
flag=1;
a=getchar();
}
while(a>='0' && a<='9'){
input=input*10+a-'0';
a=getchar();
}
gender[input]=flag; //upgrade gender[] before exit
return input;
}
int main(){
int n, m, k, cnt, a, b;
double pa_max=0.0, pb_max=0.0;
scanf("%d%d",&n,&m);
vector<vector<int> > p(n); //photos
vector<double> pa(n,0.0), pb(n,0.0); //buckets, pa[person-id] = intimacy between a & person-id
for(unsigned int i=0;i<m;++i){ //read photos
scanf("%d",&cnt);
p[i].resize((unsigned int)cnt);
for(unsigned int j=0;j<cnt;++j)
p[i][j]=read();
}
a=read(), b=read();
for(unsigned int i=0;i<m;++i){
bool founda=find(p[i].begin(),p[i].end(),a)!=p[i].end(); //if this photo has a
bool foundb=find(p[i].begin(),p[i].end(),b)!=p[i].end(); //if this photo has b
if(founda || foundb){
for(unsigned int j=0;j<p[i].size();++j){
if(founda && gender[a]!=gender[p[i][j]]){ //if found a && current assessing person-id (p[i][j]) has a different gender from a's
pa[p[i][j]]+=(double)1/p[i].size();
pa_max=max(pa_max,pa[p[i][j]]);
}else if(foundb && gender[b]!=gender[p[i][j]]){ //else found b && current assessing person-id (p[i][j]) has a different gender from b's
pb[p[i][j]]+=(double)1/p[i].size();
pb_max=max(pb_max,pb[p[i][j]]);
}
}
}
}
if(pa_max==pa[b] && pb_max==pb[a]) //if a & b are each other's most intimate person
printf("%s%d %s%d\n",gender[a]?"-":"",a,gender[b]?"-":"",b);
else{
for(unsigned int i=0;i<n;++i){
if(pa[i]==pa_max)
printf("%s%d %s%d\n",gender[a]?"-":"",a,gender[i]?"-":"",i);
}
for(unsigned int i=0;i<n;++i){
if(pb[i]==pb_max)
printf("%s%d %s%d\n",gender[b]?"-":"",b,gender[i]?"-":"",i);
}
}
return 0;
}
Ⅴ:小结
2018年的LV2进阶题还是比较容易的。做题要细心,灵活,合理用STL大法。希望2019也是如此。。
基础数据结构(STL大法) + 一点点图论(邻接表、连通分量、dfs、bfs、并查集)
细心一点!


