费马小定理 几道例题

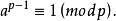
0-1:a^(p-1)与1关于p同余

可以用来降幂

a^n%p=a(n%(p-1))%p;

0-2:求a的n次方，可以先n%(p-1)。

1-1 例题：

因为模数是101，比较小，而幂n是2019^2019，很大！所以使用费马小降幂n%(p-1)，这里p就是101-1 = 100；

    int n = 1, ans = 0;
    for (int i = 1; i <= 2019; i++) {
        n = n * 2019 % 100;
    }

完整代码：

#include <iostream>
#include <algorithm>
using namespace std;
int main() {
    int n = 1, ans = 0;
    for (int i = 1; i <= 2019; i++) {
        n = n * 2019 % 100;
    }
    for (int i = 1; i <= 11; i++) {
        int x = 1;
        for (int j = 1; j <= n; j++) {
            x = x * i % 101;
        }
        ans = ans + x;
    }
    printf("%d\n", ans % 101);
    return 0;
}

1-2 例题

这道题可以不用费马小，和上题作对比

项数比mod大很多，2019比10086小，所以不用费马小，用循环周期做

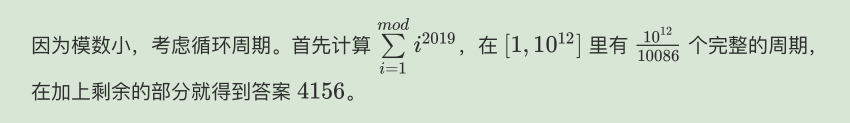
标程

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = 10086;
LL pow_mod(LL x, LL p) {
    LL res = 1;
    while (p) {
        if (p & 1) res = res * x % mod;
        p >>= 1;
        x = x * x % mod;
    }
    return res;
}
int main() {
    LL ans = 0;
    LL tmp = 1e12;
    for (int i = 1; i <= mod; i++) {
        ans = (ans+pow_mod(i, 2019))%mod;//求到10086 一个循环的长度
    }
    ans = ans * (tmp / mod) % mod;//乘上倍数
    tmp %= mod;
    for (int i = 1; i <= tmp; i++) {
        ans = (ans + pow_mod(i, 2019)) % mod; //再加上余数
    }
    printf("%lld\n", ans);
    return 0;
}

2-1：其他

其他参考博客，https://blog.csdn.net/zcy_2016/article/details/55054146