树形dp|无根树转有根树|2015年蓝桥杯生命之树

2015年蓝桥杯第十题——生命之树（无根树dfs）

①暴力解法：枚举子集（选点） + dfs判断连通性（题目要求连通）满足上面两个条件下找出最大值权值和

②dfs无根树转有根树，递归找最优

先学习无根树转有根树

参考博客：https://blog.csdn.net/Originum/article/details/82258450
参考博客：https://www.cnblogs.com/yspworld/p/4270876.html

无根树转有根树模板

void dfs(int cur, int father) {
    for (int i = 0; i < tree[cur].size(); i++) {
        int son = tree[cur][i].v;
        if (son != father) {
            dfs(son, cur);
            //
        }
    }
}

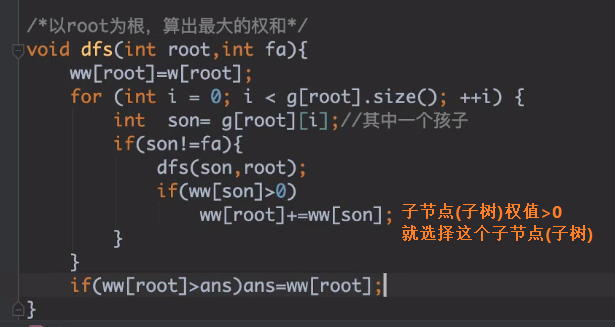
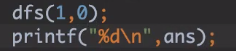
这道题思路：从根（任选一个作为根）出发，自根向下递归、自下向上回溯，选取最优（dp），每个节点都有两种选择（要、不要这个点）
无根树的每个节点是平等的，选不同的根没有区别。

代码：树上找最优

3.树形dp

学习视频：https://www.bilibili.com/video/av12194537?from=search&seid=7177934246567735469

代码参考

使用dp数组存放 选当前节点和不选当前点的两种状态

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int v[100004];
int dp[100004][2];//表示选择了当前节点和不选择的最大分数
int vis[100004];
vector<int> node[100004];
void dfs(int t)
{
	dp[t][1] = v[t];
	dp[t][0] = 0;
	vis[t] = 1;
	for (int i = 0; i < node[t].size(); i++)
	{
		if (!vis[node[t][i]])//如果这个节点没有走过的话
		{
			dfs(node[t][i]);//继续往下寻找子节点
			dp[t][1] += max(dp[node[t][i]][0], dp[node[t][i]][1]);//+=是表示选当前节点时，当前节点加上当前节点的子节点的最大序列和
		}
		else//这个子节点是不能走的
		{
			dp[t][1] = max(dp[t][1], v[t]);//所以就比较当前序列和与当前节点的分值的大小比较
			dp[t][0] = max(dp[t][0], 0);
		}
	}
}
int main()
{
	int n;
	cin >> n;
	memset(vis, 0, sizeof(vis));
	for (int i = 1; i <= n; i++)
	{
		cin >> v[i];//输入分数
	}
	int u, v;
	for (int i = 1; i < n; i++)
	{
		cin >> u >> v;
		node[u].push_back(v);
		node[v].push_back(u);
	}
	dfs(1);
	int ans = -99999;
	for (int i = 1; i <= n; i++)
	{
		ans = max(dp[i][1], ans);
		ans = max(dp[i][0], ans);
	}
	cout << ans << endl;
	system("pause");
	return 0;
}

另外一道类似的树形dp例题：没有上司的舞会

思路

代码