带权并查集|连通、集合最值、集合元素个数、到根的距离、等级辈分
带权并查集
两道题合起来,说清楚并查集的作用有哪些
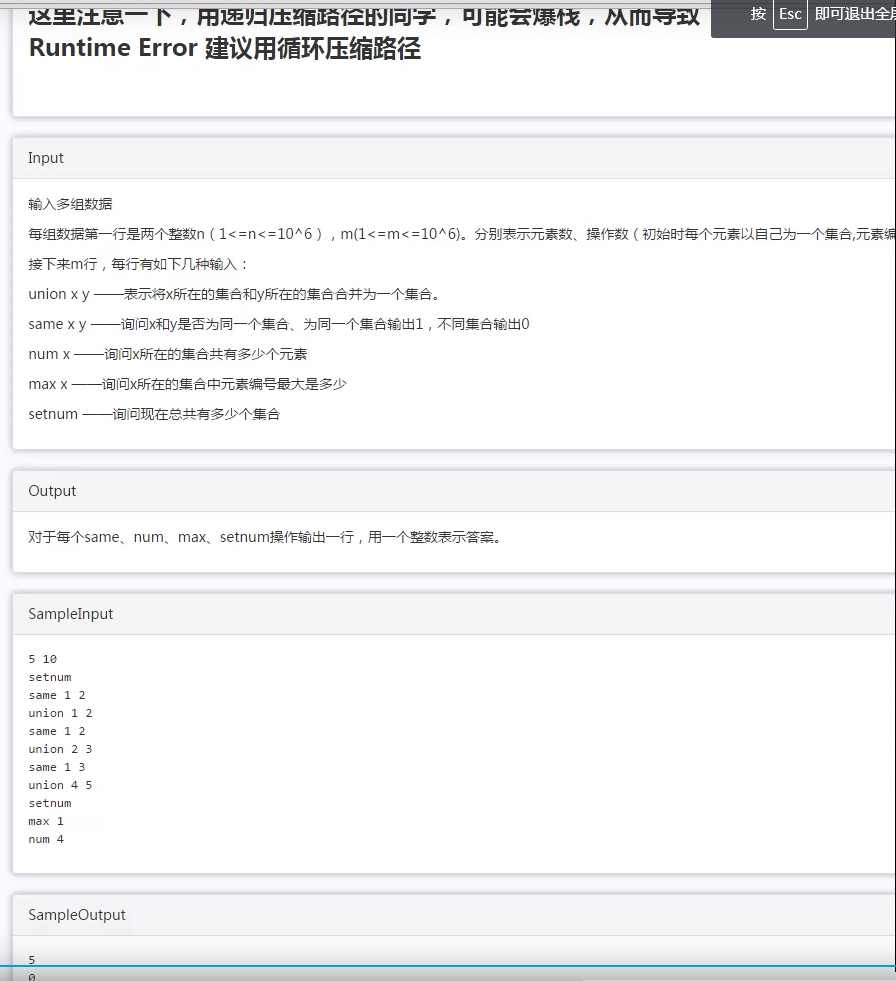
①连通、集合最值、集合元素个数、到根的距离...

#include<bits/stdc++.h>
using namespace std;
/*查找、合并|统计集合个数、集合最大值、每个集合的元素个数、到根的距离*/
const int maxn = 1e6+10;
int n,m;
int father[maxn];
int size[maxn];//集合中元素的个数
int maxs[maxn];//集合中最大值
int dist[maxn];//到根节点的距离
int setNums = 0;
void init(){
for(int i=1;i<=n;i++){
father[i] = i;
size[i] = 1;
maxs[i] = i;
dist[i] = 0;
}
}
//find循环写法
int Find(int x){
int p,tmp;
p = x;
while(father[x] != x){
x = father[x];//找到祖先节点
}
while(p!=x){//更新p(原x)的父辈节点 的父辈为祖先(x)
tmp = father[p];
father[p] = x;
p = tmp;
}
return x;
}
//递归写法
int find(int x){
if(father[x] == x){
return x;
}
int y = father[x];
father[x] = find(y);
dist[x] += dist[y];//更新x到根节点的距离
return father[x];
}
//合并
void join(int x,int y){
int a = find(x);
int b = find(y);
if(a!=b){
father[a] = b;
dist[a] = size[b];//更新子集合的根到 父集合根 的距离
size[b] += size[a];//更新父亲集合的元素个数
maxs[b] = max(maxs[a],maxs[b]);
}
}
int main(){
cin>>n>>m;//元素数 操作数
init();
char ins[20];
setNums = n;
for(int i=0;i<m;i++){
int x,y;
scanf("%s",ins);
if(ins[0] == 'u'){
cin>>x>>y;
if(find(x) != find(y)){
join(x,y);//合并
setNums--;//合并一次 集合数-1
}
}else if(ins[0] == 's' && ins[1] == 'a'){
cin>>x>>y;
int fx = find(x);
int fy = find(y);//查找是否连接 (在同一集合)
if(fx==fy) cout<<1<<endl;
else cout<<0<<endl;
}else if(ins[0] == 'n'){
cin>>x;
cout<<size[find(x)]<<endl;//查询当前集合中元素的数量
}else if(ins[0] == 'm'){
cin>>x;
cout<<maxs[find(x)]<<endl;//查询当前集合中的最大值
}else if(ins[0] == 's' && ins[1] =='e'){
cout<<setNums<<endl;//查询 集合总数
}else{
cin>>x;
find(x);
cout<<dist[x]<<endl;//打印x到它的集合的根 的距离
// cout<<size[x]-1-dist[x]<<endl;//查询排(与根的距离)在与x同一集合中 x后的有多少人
}
}
return 0;
}
②另外一类,求辈分(等级)问题,也可以用并查集做(路径压缩find函数中记录rank等级)。就是建一颗树,dfs、bfs都可以完成。
2016天梯赛

2018天梯赛
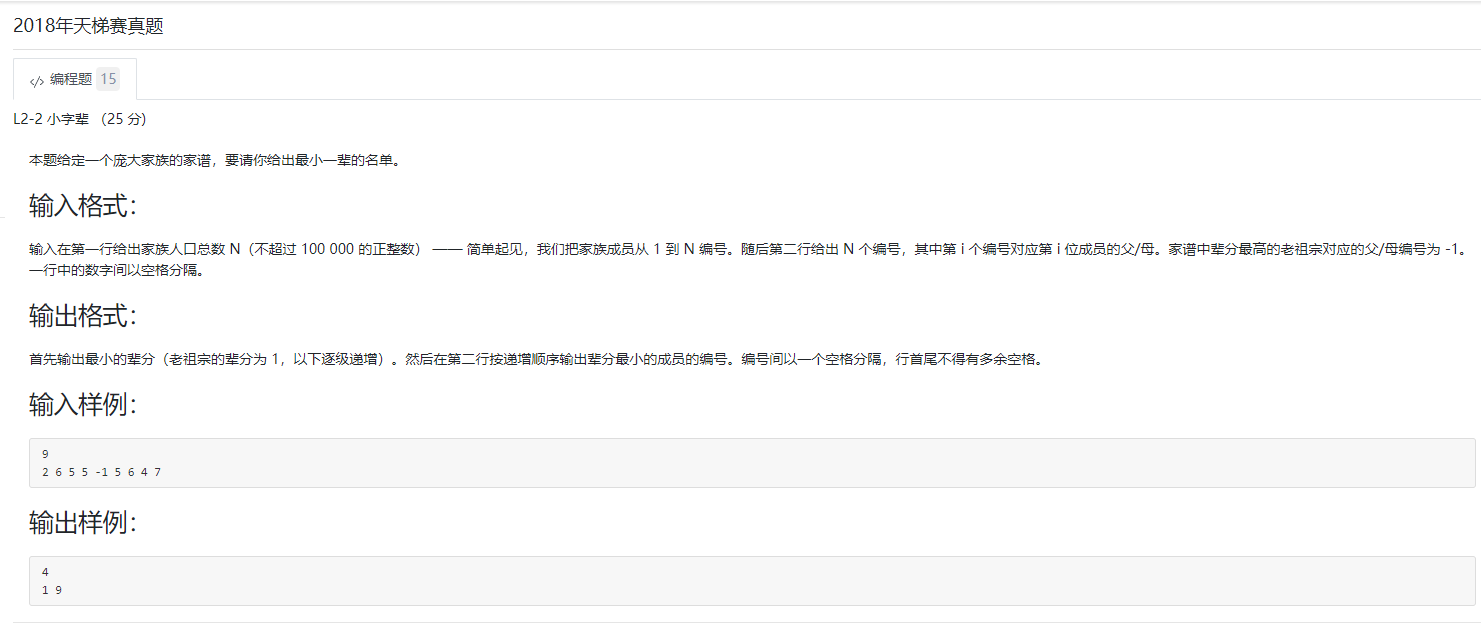
2018找辈分等级代码:
并查集
#include <iostream>
#include <vector>
using namespace std;
const int maxn=1e6 + 10;
int father[maxn];//记录父辈
int rank[maxn];//记录等级
int vis[maxn];//标记是否查询过
vector<int> vt[maxn];//存储每个辈分级别下的 元素
//路径压缩 递归累加rank等级
int find(int x)
{
if(vis[x])
return rank[x];
vis[x]=1;
if(x!=-1)//不是根节点
rank[x] += find(father[x]);//等级 加上 父亲节点的辈分
return rank[x];
}
int main()
{
int n;
cin>>n;
for(int i=1;i<maxn;i++)
{
father[i]=i;
rank[i]=1;
}
for(int i=1;i<=n;i++)
{
int k;
scanf("%d",&k);
father[i]=k;
}
int max1=-1;
for(int i=1;i<=n;i++)
{
int kk=find(i);
if(kk>max1)
{
max1=kk;
vt[max1].push_back(i);
}
else if(kk==max1)
vt[max1].push_back(i);
}
printf("%d\n",max1);
for(int i=0;i<vt[max1].size();i++)
{
if(!i) printf("%d",vt[max1][i]);
else printf(" %d",vt[max1][i]);
}
return 0;
}
bfs
#include<bits/stdc++.h> //L2-026. 小字辈(bfs stl)
using namespace std; //没什么好讲的 就bfs
const int maxn = 1e5 + 5;//虽然队友简单粗暴递归dfs也过了 限时是真的宽容啊
int level[maxn], fat[maxn];//这个fat原来是想辅助标记父亲节点的 后来发现不用了
set<int>ans, son[maxn];//简单粗暴set存儿子节点和答案 stl大法好
int main(){
int n, fa, i, maxl, t, top, f;
cin >> n;
for(i = 1; i <= n; i ++){//读入 全部把对应的子节点扔到对应的set里
cin >> t;
if(t == -1)
fa = i;
else{
fat[i] = t;
son[t].insert(i);
}
}
level[fa] = 1;
queue<int>q;
q.push(fa);
maxl = 1;
while(!q.empty()){//bfs一遍 找到最小辈分
top = q.front();
q.pop();
set<int>::iterator it;
for(it = son[top].begin(); it != son[top].end(); it ++){
q.push(*it);
level[*it] = level[top] + 1;
}
maxl = max(maxl, level[top]);
// cout << top << " ";
}
//for(i = 1; i <= n ; i ++)
// cout << level[i] << " ";
cout << maxl << endl;
f = 0;
q.push(fa);//注意这个push
while(!q.empty()){//再bfs一遍 存答案排序
top = q.front();
q.pop();
set<int>::iterator it;
for(it = son[top].begin(); it != son[top].end(); it ++){
q.push(*it);
}
if(level[top] == maxl)
ans.insert(top);
}
set<int>::iterator it;//输出
for(it = ans.begin(); it != ans.end(); it ++){
if(f) cout << " ";
else f = 1;
cout << *it;
}
return 0;
}
dfs
#include <iostream>
#include <vector>
#include <set>
using namespace std;
int maxlevel = 1;
vector<int > v[100010];
set<int> s;
void dfs(int node, int level) {
if (level > maxlevel) {
maxlevel = level;
s.clear();
s.insert(node);
} else if (level == maxlevel) {
s.insert(node);
}
for (int i = 0; i < v[node].size(); i++)
dfs(v[node][i], level+1);
}
int main() {
int n, num, root = 0;
cin >> n;
// v.resize(n+1);
for (int i = 1; i <= n; i++) {
cin >> num;
if (num == -1) {
root = i;
continue;
}
v[num].push_back(i);
}
dfs(root, 1);//从根出发建树
cout << maxlevel << endl;
for (set<int>::iterator it = s.begin(); it != s.end(); it++) {
if (it != s.begin()) cout << " ";
cout << *it;
}
return 0;
}


