棋子等级|树状数组单点更新

棋子等级

坐标系平面上有好多棋子，每个整点上至多有一个棋子。
假定棋子的等级是左下方的棋子个数，现在给出若干棋子的位置，求不同等级的棋子各有多少个。左下方包含正下和正左。说明（0，0）坐标的位置在左下角。
输入格式
第一行一个整数N（1≤N≤100000）接下来N行，一行两个整数X，Y（0≤X，Y<100000），表示坐标。
数据保证坐标先按Y排序，再按X排序。
输出格式
N行，每行一个整数，从0到N-1等级的棋子数量。

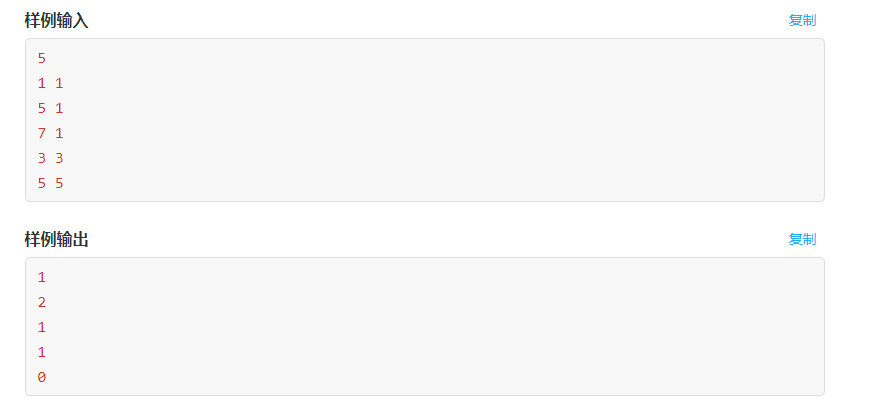
思路：Y不断增大，所以可以使用树状数组维护“横坐标小于x的棋子数量”。另外注意当x==0的时候 ，change更新函数会死循环，因此需要判断0

代码：

#include<bits/stdc++.h>
using namespace std;

const int MAX_N = 100000 + 5;
int n;
int C[MAX_N]; 
int cnt[MAX_N];
 
int lowbit(int x){
	return x & -x;
}

//求和:各个横坐标下的棋子数量----棋子等级 
int getsum(int x){
	int res = 0;
	while(x){
		res += C[x];
		x -= lowbit(x);	
	}
	return res;
}

//更新 
void change(int x,int c){
	//注意:change(x=0)的时候程序会死循环
	if(x==0){
		C[x] += c;
		x++;
	} 
	while(x<=MAX_N){
		C[x] +=c;
		x += lowbit(x);
	}
}

int main(){
	scanf("%d",&n);
	for(int i=0;i<n;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		cnt[getsum(x)]++;
		change(x,1);//小于x的横坐标上 数量加1 
	}
	//查询每个 x上的点管辖范围内的 棋子数量 
	for(int i=0;i<=n-1;i++){
		printf("%d\n",cnt[i]);
	}
	return 0;
}