剪格子|2013年蓝桥杯A组题解析第九题-fishers

剪格子

如图p1.jpg所示，3 x 3 的格子中填写了一些整数。

我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是60。

本题的要求就是请你编程判定：对给定的m x n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。
如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。   
如果无法分割，则输出 0

程序输入输出格式要求：
程序先读入两个整数 m n 用空格分割 (m,n<10)
表示表格的宽度和高度
接下来是n行，每行m个正整数，用空格分开。每个整数不大于10000
程序输出：在所有解中，包含左上角的分割区可能包含的最小的格子数目。

例如：
用户输入：
3 3
10 1 52
20 30 1
1 2 3

则程序输出：
3

再例如：
用户输入：
4 3
1 1 1 1
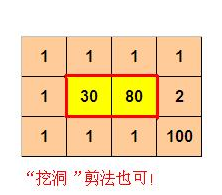
1 30 80 2
1 1 1 100

则程序输出：
10

(参见p2.jpg)

资源约定：
峰值内存消耗 < 64M
CPU消耗 < 5000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

思路：dfs回溯+可行性剪枝，搜索：是否选当前格子

代码：

#include<bits/stdc++.h>
using namespace std;

int dr[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
int all = 0;
int ans = 99999;
int n,m;
int a[15][15];
int vst[15][15];

bool in(int x,int y){
	return x >= 0 && x < n && y>=0 && y<m; 
}

void dfs(int p,int k,int x,int y){
	
	if(p*2 > all){
		return;
	}
	if(p*2 == all){
		//含左上角格子的那个区域包含的格子的最小数目。
		//是否包含 
		if(ans > k){
			if(vst[0][0] == 1){
				ans = k;
			}
		}
		return;
	}
	vst[x][y] = 1;//当前搜寻的是 x y坐标 所以回溯x和y 
	for(int i=0;i<4;i++){
		int tx = x + dr[i][0];
		int ty = y + dr[i][1];
		if(in(tx,ty) && !vst[tx][ty]){
			dfs(p+a[x][y],k+1,tx,ty);
		}
	}
	vst[x][y] = 0;
}




int main(){
	scanf("%d%d",&m,&n);
	for(int i=0;i<n;i++){
		for(int j=0;j<m;j++){
			scanf("%d",&a[i][j]);
			all += a[i][j];
		}
	}
	dfs(0,0,0,0);
	
	if(ans == 99999 ) printf("%d\n",0);
	else printf("%d\n",ans); 
	return 0;
}