差分数组|小a的轰炸游戏-牛客317E
小a的轰炸游戏
题目链接:https://ac.nowcoder.com/acm/contest/317/E
思路
这题考查的是对差分数组原理和前缀和的理解。
四个数组分别记录朝着四个方向下放的个数最后求个前缀,就代表着这一行中从这个点开始作为起点的轰炸区域个数,四个数组分别向着四个方向下放最终得到的四个数组分别是前。
4个数组对应下面4条箭头:
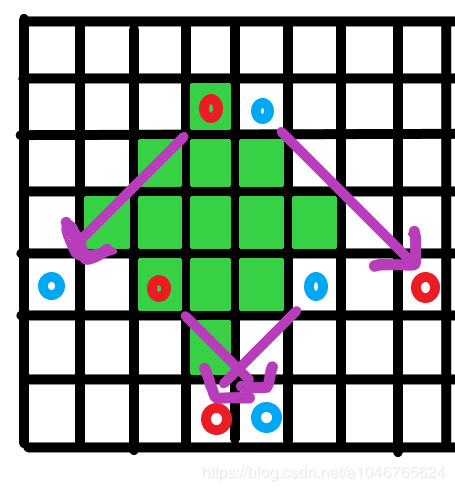
图中的绿色是要进行区间操作的菱形。红色圆圈是打的+1操作,蓝色圆圈是打的-1操作。它们是成对出现的,每个红色圆圈都有一个蓝色圆圈来消除它。 它们的标记传递方向是那个紫色的箭头。所以有四种传递方向。就要有四个标记数组。这样传递的话就可以按行遍历,边遍历边下传。
在矩形中,我们在四个角上进行++--,然后利用差分的性质,就解决了区间更新,因为矩形的差分是横着或者竖着的,最后的求和非常容易,但是这里不一样。最后看了题解豁然大悟,原来差分还可以动态的来,本行的差分数组使用完了,还可以把差分数组下传,继续在下一层继续起到作用。
由于可能出现越界的情况,但是标记还是需要处理的。所以就要加个偏移量来进行处理,但是最后计算,只是算原来的矩形。
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<string>
#include<cmath>
#include<cstring>
#define ll long long
#define pb push_back
#define pm make_pair
#define fi first
#define se second
using namespace std;
const int MAX = 3030,ADD = 1000; //ADD表示偏移量 防止越界
int a[MAX][MAX],b[MAX][MAX],c[MAX][MAX],d[MAX][MAX]; //abcd4个数组分别表示4个方向
//上半部分
void up(int x,int y,int l) {
a[x-l/2][y]++,b[x-l/2][y+1]--;
a[x+1][y-l/2-1]--,b[x+1][y+l/2+2]++;
}
//下半部分
void down(int x,int y,int l){
c[x+1][y-l/2+1]++,d[x+1][y+l/2]--;
c[x+l/2+1][y+1]--,d[x+l/2+1][y]++;
}
int main() {
int n,m,q;
cin>>n>>m>>q;
for(int op,x,y,l,i = 1; i<=q; i++) {
scanf("%d%d%d%d",&op,&x,&y,&l);
x+=ADD,y+=ADD; //加上偏移量 防止越界
if(op == 1) up(x,y,l),down(x,y,l);
if(op == 2) up(x,y,l);
}
//差分数组 差分传递
for(int i = 1; i<=n+ADD*2; i++) {
for(int j = 1; j<=m+ADD*2; j++) {
a[i][j] += a[i-1][j+1];
b[i][j] += b[i-1][j-1];
c[i][j] += c[i-1][j-1];
d[i][j] += d[i-1][j+1];
}
}
//计算异或和
int ans = 0;
for(int i = 1; i<=n+ADD*2; i++) {
int tmp = 0;
for(int j = 1; j<=m+ADD*2; j++) {
tmp += a[i][j] + b[i][j] + c[i][j] + d[i][j];
if(i>=ADD+1 && i<=ADD+n && j>=ADD+1 && j<=ADD+m) ans ^=tmp;
}
}
cout << ans <<endl;
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号