夺冠概率|2012年蓝桥杯B组题解析第九题-fishers

9. (17')夺冠概率

   足球比赛具有一定程度的偶然性，弱队也有战胜强队的可能。
   假设有甲、乙、丙、丁四个球队。根据他们过去比赛的成绩，得出每个队与另一个队对阵时取胜的概率表:

   甲 乙 丙 丁
   甲 - 0.1 0.3 0.5
   乙 0.9 - 0.7 0.4
   丙 0.7 0.3 - 0.2
   丁 0.5 0.6 0.8 -

   数据含义：甲对乙的取胜概率为0.1，丙对乙的胜率为0.3，...
   现在要举行一次锦标赛。双方抽签，分两个组比，获胜的两个队再争夺冠军。（参见【1.jpg】）

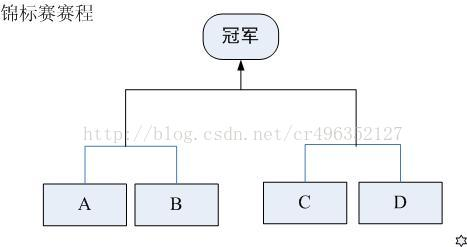
请你进行10万次模拟，计算出甲队夺冠的概率。

思路：题目给出了甲乙丙丁相互之间竞争取胜的各自的概率。现在要求模拟10万次比赛，求出甲队夺冠的概率，甲获胜比赛安排的类型是有限的。如下图：

一共有这三种情况，而这三种情况甲夺冠的概率可以分别求出来，这三个概率相加就是甲夺冠的理论概率（这个值是恒定的，因为这三种情况出现的概率都是1/3），但是题目让模拟10万次，那么每次得出的概率一定不是相同的，但是都是非常接近这个恒定的概率值。我们可以是使用rand()函数，随机获取0-2这三个数，用来体现这三种情况出现的随机性，10万次的概率总和相加，最后除以10万即是答案。

代码：

#include<cstdio>
#include<ctime>
#include<cstdlib>
using namespace std;
double p[3];
int main(){
	//三种情况的概率 
	p[0] = 0.1*0.8*0.5 + 0.1*0.2*0.3;
	p[1] = 0.3*0.6*0.5 + 0.3*0.4*0.1;
	p[2] = 0.5*0.7*0.1 + 0.5*0.3*0.3;
	//用来记录10万次概率的总和 
	double sum = 0;
	//设置随机数种子 
	srand(time(NULL));
	for(int i=1 ;i<=100000 ;i++){
		int r = rand()%3;
		sum += p[r];
	} 
	printf("%f\n",sum/100000);
	return 0;
}