放棋子|2012年蓝桥杯B组题解析第七题-fishers
- (13')放棋子
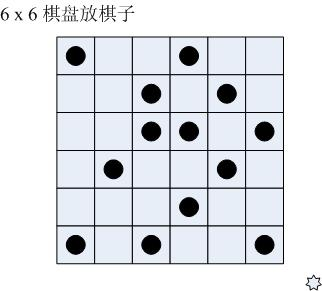
今有 6 x 6 的棋盘格。其中某些格子已经预先放好了棋子。现在要再放上去一些，使得：每行每列都正好有3颗棋子。我们希望推算出所有可能的放法。下面的代码就实现了这个功能。
初始数组中，“1”表示放有棋子，“0”表示空白。
int N = 0;
bool CheckStoneNum(int x[][6])
{
for(int k=0; k<6; k++)
{
int NumRow = 0;
int NumCol = 0;
for(int i=0; i<6; i++)
{
if(x[k][i]) NumRow++;
if(x[i][k]) NumCol++;
}
if(_____________________) return false; // 填空
}
return true;
}
int GetRowStoneNum(int x[][6], int r)
{
int sum = 0;
for(int i=0; i<6; i++) if(x[r][i]) sum++;
return sum;
}
int GetColStoneNum(int x[][6], int c)
{
int sum = 0;
for(int i=0; i<6; i++) if(x[i][c]) sum++;
return sum;
}
void show(int x[][6])
{
for(int i=0; i<6; i++)
{
for(int j=0; j<6; j++) printf("%2d", x[i][j]);
printf("\n");
}
printf("\n");
}
void f(int x[][6], int r, int c);
void GoNext(int x[][6], int r, int c)
{
if(c<6)
_______________________; // 填空
else
f(x, r+1, 0);
}
void f(int x[][6], int r, int c)
{
if(r==6)
{
if(CheckStoneNum(x))
{
N++;
show(x);
}
return;
}
if(______________) // 已经放有了棋子
{
GoNext(x,r,c);
return;
}
int rr = GetRowStoneNum(x,r);
int cc = GetColStoneNum(x,c);
if(cc>=3) // 本列已满
GoNext(x,r,c);
else if(rr>=3) // 本行已满
f(x, r+1, 0);
else
{
x[r][c] = 1;
GoNext(x,r,c);
x[r][c] = 0;
if(!(3-rr >= 6-c || 3-cc >= 6-r)) // 本行或本列严重缺子，则本格不能空着！
GoNext(x,r,c);
}
}
int main(int argc, char* argv[])
{
int x[6][6] = {
{1,0,0,0,0,0},
{0,0,1,0,1,0},
{0,0,1,1,0,1},
{0,1,0,0,1,0},
{0,0,0,1,0,0},
{1,0,1,0,0,1}
};
f(x, 0, 0);
printf("%d\n", N);
return 0;
}
思路：题意放棋子就是dfs搜索，搜索每一行每一列下是否能放棋子，什么时候能放棋子是使用GetRowStoneNum和GetColStone两个函数判断是否行列分别小于3，当前格子放完棋子后是使用GoNext函数寻找下一个能放棋子的位置。最后递归程序若到了递归出口 r==6时 判断棋盘是否满足了条件（调用CheckStoneNum函数）
答案：NumRow!=3 || NumCol !=3 和 f(x,r,c+1) 和 x[r][c]
最后放上一份完整的代码（带注释）：
#include<stdio.h>
#include<iostream>
#include<stdlib.h>
using namespace std;
int N = 0;
//检查棋盘是否合法
bool CheckStoneNum(int x[][6])
{
for(int k=0; k<6; k++)
{
int NumRow = 0;
int NumCol = 0;
for(int i=0; i<6; i++)
{
if(x[k][i]) NumRow++;
if(x[i][k]) NumCol++;
}
// 填空
if(NumRow!=3 || NumCol !=3) {
return false;
}
}
return true;
}
//统计当前行上的棋子数量
int GetRowStoneNum(int x[][6], int r)
{
int sum = 0;
for(int i=0; i<6; i++) if(x[r][i]) sum++;
return sum;
}
//统计当前列上的棋子数量
int GetColStoneNum(int x[][6], int c)
{
int sum = 0;
for(int i=0; i<6; i++) if(x[i][c]) sum++;
return sum;
}
//展示棋盘
void show(int x[][6])
{
for(int i=0; i<6; i++)
{
for(int j=0; j<6; j++) printf("%2d", x[i][j]);
printf("\n");
}
printf("\n");
}
void f(int x[][6], int r, int c);
//找到下一个放棋子的位置
void GoNext(int x[][6], int r, int c)
{
if(c<6){
f(x,r,c+1); // 填空 递归搜索下一列
}
else
f(x, r+1, 0); //递归搜索下一行的第0列
}
//递归主程序
void f(int x[][6], int r, int c)
{
//如果到了最后一行放完
if(r==6)
{
//检查是否满足
if(CheckStoneNum(x))
{
//计数 显示数据
N++;
show(x);
}
return;
}
//填空
if(x[r][c]) // 已经放有了棋子
{
GoNext(x,r,c);
return;
}
int rr = GetRowStoneNum(x,r); //取得当前行上 放的数量
int cc = GetColStoneNum(x,c); //取得当前列上 放的数量
if(cc>=3) // 本列已满
GoNext(x,r,c);
else if(rr>=3) // 本行已满
f(x, r+1, 0);
else
{
x[r][c] = 1;
GoNext(x,r,c);
x[r][c] = 0;
if(!(3-rr >= 6-c || 3-cc >= 6-r)) // 本行或本列严重缺子，则本格不能空着！
GoNext(x,r,c);
}
}
int main(int argc, char* argv[])
{
int x[6][6] = {
{1,0,0,0,0,0},
{0,0,1,0,1,0},
{0,0,1,1,0,1},
{0,1,0,0,1,0},
{0,0,0,1,0,0},
{1,0,1,0,0,1}
};
f(x, 0, 0);
printf("%d\n", N);
return 0;
}
