螺旋折线|2018年蓝桥杯B组题解析第七题-fishers

标题：螺旋折线

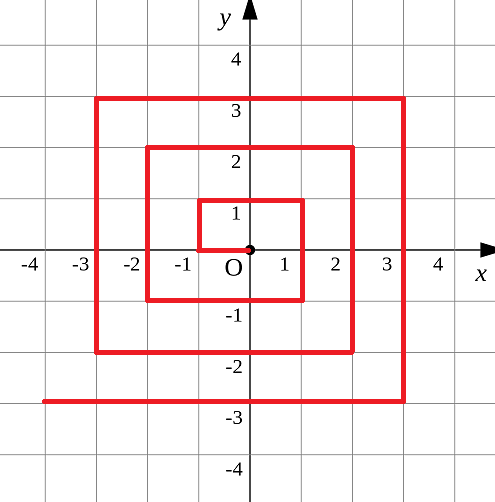
如图p1.png所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。

例如dis(0, 1)=3, dis(-2, -1)=9

给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？

【输入格式】
X和Y

对于40%的数据，-1000 <= X, Y <= 1000
对于70%的数据，-100000 <= X， Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000

【输出格式】
输出dis(X, Y)

【样例输入】
0 1

【样例输出】
3

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

注意：
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include
不能通过工程设置而省略常用头文件。

提交程序时，注意选择所期望的语言类型和编译器类型。

思路：模拟螺旋折线 从0,0开始 左上右下

代码：

#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;

int X,Y;
//模拟螺旋折线 从0,0开始 左上右下 

int main(){
	int arr[200][200];
	memset(arr,0,sizeof(arr));
	arr[0][0] = 0;
	cin>>X>>Y;
	int t = max(abs(X),abs(Y));
	int i = 0,j = 0;
	int ans = 0;
	for(int x=0,y=0;x<=t,y<=t;x++,y++){
		//左走一次到底 
		while(i>-x-1){
			i--;
			ans +=1;
			arr[i][j] = ans;
			if(i == X && j == Y){
				cout<<ans<<endl;
				return 0;
			}
		}
			
		//上走到底 
		while(j<y+1){
			j++; 
			ans +=1;
			arr[i][j] = ans;
			if(i == X && j == Y){
				cout<<ans<<endl;
				return 0;
			}
		}
		
		//右 
		while(i<x+1){
			i++;
			ans+=1;
			arr[i][j] = ans;
			if(i == X && j == Y){
				cout<<ans<<endl;
				return 0;
			}
		}	
	
		//下 
		while(j>-y-1){
			j--;
			ans+=1;
			arr[i][j] = ans;
			if(i == X && j == Y){
				cout<<ans<<endl;
				return 0;
			}
		}
	}
	return 0;
}