深度学习Momentum(动量方法)

转自：http://blog.csdn.net/bvl10101111/article/details/72615621

先上结论：

1.动量方法主要是为了解决Hessian矩阵病态条件问题（直观上讲就是梯度高度敏感于参数空间的某些方向）的。

2.加速学习 

3.一般将参数设为0.5,0.9，或者0.99，分别表示最大速度2倍，10倍，100倍于SGD的算法。

4.通过速度v，来积累了之前梯度指数级衰减的平均，并且继续延该方向移动： 

 

再看看算法： 

动量算法直观效果解释：

  如图所示，红色为SGD+Momentum。黑色为SGD。可以看到黑色为典型Hessian矩阵病态的情况，相当于大幅度的徘徊着向最低点前进。 
  而由于动量积攒了历史的梯度，如点P前一刻的梯度与当前的梯度方向几乎相反。因此原本在P点原本要大幅徘徊的梯度，主要受到前一时刻的影响，而导致在当前时刻的梯度幅度减小。 
  直观上讲就是，要是当前时刻的梯度与历史时刻梯度方向相似，这种趋势在当前时刻则会加强；要是不同，则当前时刻的梯度方向减弱。 

 

从另一个角度讲：

  要是当前时刻的梯度与历史时刻梯度方向相似，这种趋势在当前时刻则会加强；要是不同，则当前时刻的梯度方向减弱。 
  假设每个时刻的梯度g总是类似，那么由我们可以直观的看到每次的步长为： 

 
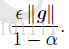
即当设为0.5,0.9，或者0.99，分别表示最大速度2倍，10倍，100倍于SGD的算法。