L1正则与L2正则

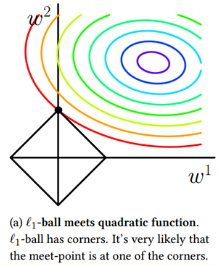
L1正则是权值的绝对值之和，重点在于可以稀疏化，使得部分权值等于零。

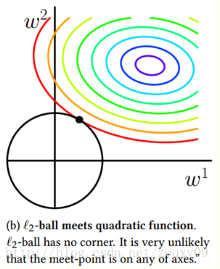
L1正则的含义是 ∥w∥≤c，如下图就可以解释为什么会出现权值为零的情况。

 

 

L1正则在梯度下降的时候不可以直接求导，可以有以下几种方法来优化

1.OWL-QN算法http://blog.csdn.net/google19890102/article/details/47424845

对于目标函数中包含加性的非平滑项并使用梯度下降求解的问题，如果可以使用proximal operator，则解法如下：

假设目标函数为 \min_x f(x) + h(x) 其中 f(x) 可导，而 h(x) 不可导。
则每步迭代更新为 x^{k+1} = Prox_{h,\eta}(x^k - \eta\triangledown f(x^k))
其中，Prox_{h,\eta} (x) = \arg\!\min_y \frac{1}{2\eta}\|y - x\|^2 + h(y)
如果 h(x) = \|x\|_1，也就是题目中要求的L1范数正则化，则对应的Prox_{h,\eta} (x) = \arg\!\min_y \frac{1}{2\eta}\|y - x\|^2 + \|x\|_1 = \hat{y}
\hat{y}_i = \begin{cases} x_i - \eta & \text{if}\ x_i-\eta > 0 \\ x_i + \eta & \text{if}\ x_i+\eta < 0 \\ 0 & \text{otherwise} \\ \end{cases}

 2.在scikit-learn中l1正则使用坐标下降和最小角回归来实现优化的

坐标轴下降是每次固定其他维度，选择其中一个维度来更新目标函数值，遍历所有的维度，迭代多次，直到目标函数值没有发生明显变化。

L2正则的重点在于防止过拟合，没有稀疏特征的效果。L2正则在梯度下降的时候可以直接求导

∥w∥2≤c

 

 

posted @ 2017-04-12 11:15  fisherinbox  阅读(575)  评论(0)  编辑  收藏  举报