用位操作来实现求组合

引例

先来看一道题目，这个题目是理解利用位操作求组合的关键。它是POJ的2453。英文原题就不贴了，我用中文描述一下吧：给定一个正整数N，求最小的、比N大的正整数M，使得M与N的二进制表示中有相同数目的1。

上面的题目描述或许有点拗口，举个例子把，假如给定的N为78，其二进制表示为1001110，包含4个1，那么最小的比N大的并且二进制表示中只包含4个1的数是83，其二进制是1010011，因此83就是答案。那么如何求解这个问题呢？这里给出两个思路：

(1) 最直观的思路：枚举

思路是从N+1开始枚举，对每个数都测试其二进制表示中的1的个数是否与N的二进制表示中1的个数相等，遇到第一次相等时就停止。其算法流程如下：

1、  求得N的二进制表示中1的个数k;

2、  N++;

3、  测试N的二进制表示中所包含的1的个数是否等于k，如果是，则输出N后结束，否则转2；

上面的过程可以用如下的流程图来表示:

用代码实现上述流程如下：

[cpp] view plaincopy
 
 
  1. int GetNextN(unsigned int N)  
  2. {  
  3.     int k = count1Bits(N);  
  4.     do  
  5.     {  
  6.         N++;  
  7.     }while(count1Bits(N)!=k);  
  8.     return N;  
  9. }  


    上面的代码中还有一个问题没有解决，那就是“求整数的二进制表示中有多少个1”即count1Bits()函数。这个问题在我之前的《c/c++***钻问题各个击破之位运算及其实例(1)》中有详细阐述，它应用了n&=(n-1)能将n的二进制表示中的最右边的1翻转为0的事实。只需要不停地执行n&=(n-1)，直到n变成0为止，那么翻转的次数就是原来的n的二进制表示中1的个数，其代码如下：

[cpp] view plaincopy
 
 
  1. int count1Bits(unsigned int n)  
  2. {  
  3.     int count = 0;  
  4.     while(n)  
  5.     {  
  6.         count++;  
  7.         n&=(n-1);  
  8.     }  
  9.     return count;  
  10. }  


 

至此，第一个枚举方法介绍完毕，你只需要写如下的main()函数就能测试本方法：

[cpp] view plaincopy
 
 
  1. void main()  
  2. {  
  3.     int N;  
  4.     cin>>N;  
  5.     cout<<GetNextN(N)<<endl;  
  6. }  


 

     上面的方法即直观，效率也还不错，但是还有没有更好效率的算法呢？通过查阅资料，我找到了一个“非常给力的”、“通过位操作的”、“只需要一步就能求得答案的”方法。是的，我用了如此之多的形容词来美化这个方法，其实一点不为过，接下我将介绍它。

(2) 非常给力的方法

即将要介绍的方法到底有多给力呢？它神奇到只用如下几行代码(事实上可以合并为一行代码)就能实现上述所有代码的功能，这几行代码是：

[cpp] view plaincopy
 
 
  1. int NextN(int N)  
  2. {  
  3.     int x = N&(-N);        
  4.     int t = N+x;  
  5.     int ans = t | ((N^t)/x)>>2;  
  6.     return ans;  
  7. }  


 

     看到了不，这就是所有代码，如果省去临时变量，它就只包含一行代码，但是为了后面讲述方便，我将它写成三行代码。它的强大之处并非只是代码少，如你所见，它无需调用count1Bits函数(效率！)，也没有前面枚举法中GetNextN函数中的while循环(效率！)。是的，我们这里的NextN函数比之前的GetNextN函数效率要高很多，它的时间复杂度是O(1)！

如果您是大牛，请不要笑话我在这里的大惊小怪，如果你跟两三天前的我一样不懂这几句代码的话，那么请往下看，我将尝试着把我的理解详细的表述出来，力求细致，简单，易懂。

以N=78为例(其二进制表示为1001110)，我们的任务是求得最小的比N大，二进制表示中1的个数与N相同的数：83(其二进制表示为1010011)。首先我们要总结出来从78变成83的规律，为了方便，将78和83的二进制写成竖式形式：

78：1 0 0 1 1 1 0

83：1 0 1 0 0 1 1

可以看出，为了得到83，我们只需要对N(78)的二进制中最右边的连续的1位串(加粗标红)进行操作！其过程是：将连续的1位串中最左边的1向左“移动”一位，其他的1位串“移动”到最右边！这即保证了二进制表示中1的个数不变，又保证了新得到的数比原来的数大，并且是最小的。其过程可以用如下图示表示：

在上面的描述中我用引号把两个“移动”引起来了，原因是，具体实现时，我们并不是对这些二进制位进行移动，而是通过位操作来达到同样的目的，而这些位操作就是本问题的关键。接下来我将分析前面那个“非常给力的代码”看看它是如何用位操作来实现对这些位的“移动”的。

首先来看语句int x = N&(-N);它的功能是找到N(即78)的二进制表示中最右边的1(这个1必定是N的二进制表示中最右边的连续的1位串的开始)。该过程图示如下：

接下来看看int t = N+x;该语句实现了“将连续的1位串中最左边的1向左“移动”一位”的功能，当然它带来了副作用：使得连续的1位串中其他的1丢失了！其过程如下：

       最后的任务就是要将上面丢失的1补上，并放到最右边，这就是语句int ans = t | ((N^t)/x)>>2;的功能。首先，要知道需要补多少个1，通过分析可以知道需要补上的1的个数等于N的二进制表示中最右边的连续的1位串中1的个数减1，然而如果通过位操作来求得呢？这就是N^t的功能了，如下图所示，N^t的二进制表示只包含1个连续的1串，并且1的个数正好等于N的二进制表示中最右边的连续的1位串中1的个数加1：

由上面的分析可知，N^t中的1的个数实际上比我们需要补的1的个数多2！这就使得我们可以通过N^t求得需要补的1的个数，接下来的任务就是如何补上这些1了。

进步一分析得知，N^t的二进制表示中最低位的1正好与x中那个1对应，因此我们就可以通过(N^t)/x将这些1全部移到最右边了，然而此时1的个数比我们要补的个数多了2，没关系我们在把结果右移2位就可以了，也就是((N^t)/x)>>2。如此一来我们求得了要补的1的个数和其位置。本段的描述可以用下图形象地表示：

 

最后我们只需要用t | ((N^t)/x)>>2;就能得到所求之数了！其过程如下图：

以上就是我对这个非常给力的代码的分析。短短3句代码(省去中间变量的话，就一句代码)居然包含了如此之多的东西，这就是位运算的强大之处，也是位运算的难学之处。本人以前也很少关注位运算，像这样给力的代码我是写不出来的，因此我也只能按照如上步骤那么去读懂这个代码。至此，本篇的引例算是完成了，不可思议吧，为了求组合，我居然用了这么多篇幅来讲一个引例，这会不会本末倒置啊？我自信不会的，因为有了这个引例，下面求组合就太easy了。

本篇主题：利用位操作求组合

组合就是从N各对象中选取m个对象，问有多少种选法，并且要求输出每次的选法。比如给定1,2,3,4四个数，从中选择2个的选法有：{1,2}，{1,3}，{1,4}，{2,3}，{2,4}，{3,4}共6种选法。当然求组合的方法非常之多，我这里只介绍如何利用位操作来求，其思路是：用2进制bit位来标识某个对象是否被选中，1代表选中，0代表没选中。比如前面的例子的组合可以用下图来表示(最低位为1表示选中第一对象，以此类推)。

根据上面的分析，我们可以用一个包含N个bit位的数C来求N个对象中选取m个对象的组合：首先让C的最低m位全部为1(对应到从N个对象中选择前m个对象的组合情况)，然后用我们引例的方法求出最小的比C大并且二进制表示中包含的1的个数与C相同的数K,就能求得下一个组合情况。其流程如下：

1、  初始化C=(1<<m)-1；(选择N个对象中的前m个作为第一个组合)；

2、  根据C的二进制表示输出其所对应的组合；

3、  调用C=NextN(C);

4、  通过判断C是否小于等于(1<<N)-(1<<(N-m))来确定是不是输出了所有的组合(注意，当C==(1<<N)-(1<<(N-m))时，C就对应着从N个对象中选择后m个对象的组合情况，也就是最后一个组合)，如果C小于等于(1<<N)-(1<<(N-m))，则转2，否则转5；

5、  结束（已经输出所有组合）。

上面流程中的关键部分我都标粗了，如果对该流程有疑问，可以与我联系(w57w57w57@163.com)。下面我将根据上面的流程给出代码：

[cpp] view plaincopy
 
 
  1. #include <stdio.h>  
  2. #include"iostream"  
  3. using namespace std;  
  4. //定义包含4个元素的集合   
  5. char set[] ={'a','b','c','d','e','f','g','h','i'};  
  6. //根据C的二进制表示输出一个组合   
  7. void print(char* set,int C)  
  8. {  
  9.     int i = 0;  
  10.     int k;  
  11.     while((k=1<<i)<=C)  
  12.     {//循环测试每个bit是否为1   
  13.         if((C&k)!=0)  
  14.         {  
  15.             cout<<set[i];  
  16.         }  
  17.         i++;  
  18.     }  
  19. }   
  20. //这个NextN跟之前我们讨论的是一样的，只不过省去了临时变量   
  21. int NextN(int N)  
  22. {  
  23.     return (N+(N&(-N))) | ((N^(N+(N&(-N))))/(N&(-N)))>>2;  
  24. }   
  25. //求从set中前N个元素 中选择m个的组合   
  26. void Combination(char* set,int N,int m)  
  27. {  
  28.     int C = (1<<m)-1;  
  29.     while(C<=((1<<N)-(1<<(N-m))))  
  30.     {  
  31.         print(set,C);  
  32.         cout<<endl;  
  33.         C = NextN(C);  
  34.     }       
  35. }                
  36. void main()  
  37. {  
  38.     Combination(set,4,2);  
  39. }    


 

上面的代码在VC6.0中测试通过，其运行结果如下：

       最后，或许您对Combination函数中的while中的条件表达式：C<=((1<<N)-(1<<(N-m)))不理解，那么请看下图，该图示意了最后一个组合所对应的C，其值正好等于(1<<N)-(1<<(N-m))

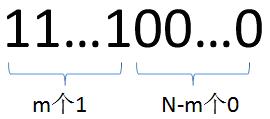
分析

由于我这里没有给出求组合数的其他算法，因此无法对该算法与其他算法的性能做对比，有兴趣的朋友可以做一个对比。事实上这个算法的效率相当之高，因为它直接根据前一个组合一步就能求得后面一个组合。当然它也并非没有一点瑕疵，我个人认为它有两点不足：

1、  由于它需要用一个整数的二进制位来标识哪些对象被选中，而整数是有范围的，因此如果N比较大(大于32)，那么该算法就不能直接利用了。

2、  得到的组合并非有序的，如上面的结果所示输出ac之后并非输出ad，而是bc，其原因是NextN(N)函数，它返回的是“最小的、比N大的、二进制表示中1的个数与N相同的数”然而这个约束并不能保证根据它求得的组合是有序的。如果一定要求有序的组合，那么，可以修改NextN这个函数，但本文的核心就是它，因此修改它很可能就失去了意义，当然您可以想出另外一个位运算，在不损失效率的情况下改变NextN的功能，从而得到有序的组合，这个也是我在思考的问题。

posted on 2015-05-31 17:43  Fishbonell  阅读(379)  评论(0)  编辑  收藏  举报
Copyright © 2024 Fishbonell
Powered by .NET 9.0 on Kubernetes Powered by: 博客园