hdu 1198 Farm Irrigation(并查集)
题意:
Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.
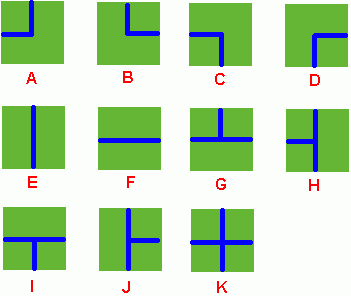
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map
ADC
FJK
IHE
then the water pipes are distributed like
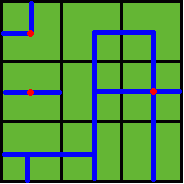
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.
Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?
There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.
思路:
并查集,看代码。
代码:
struct node{ bool up,down,left,right; } a[2505]; int m,n; char graph[55][55]; int fa[2505]; int findFa(int x){ return fa[x]==x?fa[x]:fa[x]=findFa(fa[x]); } void Union(int x,int y){ int fx=findFa(x); int fy=findFa(y); if(fx!=fy){ fa[fx]=fy; } } int main(){ while(scanf("%d%d",&m,&n),m>0||n>0){ rep(i,0,m-1) scanf("%s",graph[i]); rep(i,1,m*n) a[i].up=a[i].down=a[i].left=a[i].right=false; rep(i,0,m-1){ rep(j,0,n-1){ switch(graph[i][j]){ case 'A':a[i*n+j+1].up=true; a[i*n+j+1].left=true; break; case 'B':a[i*n+j+1].up=true; a[i*n+j+1].right=true; break; case 'C':a[i*n+j+1].left=true; a[i*n+j+1].down=true; break; case 'D':a[i*n+j+1].right=true; a[i*n+j+1].down=true; break; case 'E':a[i*n+j+1].up=true; a[i*n+j+1].down=true; break; case 'F':a[i*n+j+1].left=true; a[i*n+j+1].right=true; break; case 'G':a[i*n+j+1].left=true; a[i*n+j+1].right=true; a[i*n+j+1].up=true; break; case 'H':a[i*n+j+1].up=true; a[i*n+j+1].down=true; a[i*n+j+1].left=true; break; case 'I':a[i*n+j+1].right=true; a[i*n+j+1].left=true; a[i*n+j+1].down=true; break; case 'J':a[i*n+j+1].up=true; a[i*n+j+1].down=true; a[i*n+j+1].right=true; break; case 'K':a[i*n+j+1].up=true; a[i*n+j+1].left=true; a[i*n+j+1].down=true; a[i*n+j+1].right=true; break; default: break; } } } rep(i,1,m*n) fa[i]=i; rep(i,1,m){ rep(j,1,n){ int now=(i-1)*n+j; if(j!=1){ int last1=(i-1)*n+j-1; if(a[last1].right && a[now].left){ Union(last1,now); } } if(i!=1){ int last2=(i-2)*n+j; if(a[last2].down && a[now].up){ Union(last2,now); } } } } map<int,int> mp; mp.clear(); int ans=0; rep(i,1,m*n){ int t=findFa(i); if(mp[t]==0){ ++ans; mp[t]=1; } } printf("%d\n",ans); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号